4월 1주차 그래프 오마카세

Graph Neural Networks Inspired by Classical Iterative Algorithms

[https://arxiv.org/pdf/2103.06064.pdf]

preliminary

IRLS , Iterative Reweighted Least Squares

suggested resource ; [Medium]

IRLS is to iteratively reweight the least-squares regression problem based on the current estimates of the model parameters. The weights are chosen such that points with large residuals (i.e., large differences between the predicted and observed values) are down-weighted, while points with small residuals are up-weighted. By doing this, the algorithm focuses on fitting the model to the most informative data points.

proximal gradient descent

Gradient Descent is a basic optimization algorithm that does not incorporate any explicit regularization, Proximal Gradient Descent adds an additional proximal operator to the cost function that provides a regularization term, which can lead to improved generalization performance of the model.

summary

다음 두가지 고민을 가지고 계신 분들에게 도움이 될 논문이라 생각합니다. 1. GNN 아키텍쳐 개선을 해보고 싶은데, 어디부터 시작해야할지 고민이신분들 2. 어텐션(Attention) , 단순 내적을 통해 가중치(weight)가 전달되는데 왜 잘될까? 잘되지 않을 경우가 있을텐데, 그 잘되지 않을 경우를 어떻게 정의하고 적용할지 고민이신분들.

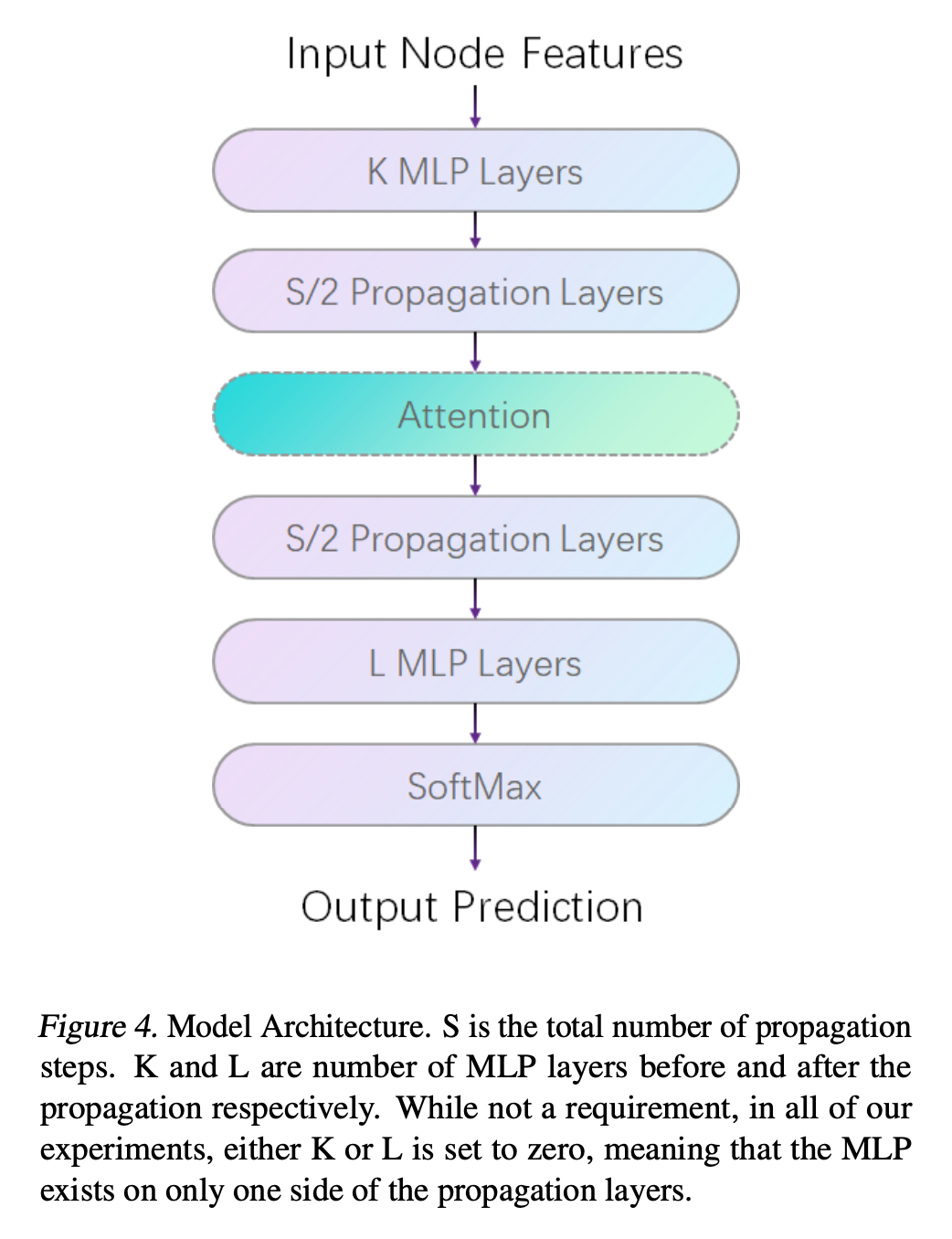
초반에 언급한 preliminary 에서 살펴본 IRLS 와 proximal gradient descent 를 활용하여 regularization term 을 iterative application 한다는게 논문의 핵심 아이디어입니다. oversmoothing, long-range dependenices , and spurious edges 세 단어들 모두 GNN의 challenging problem 인데요. 여기에서 세 문제의 공통점은 바로 ‘edge’ 라고 볼 수 있습니다. 노드간 전달되는 정보들이 너무 증폭되거나 감축하는 경우가 발생하기 때문이죠. 이 증폭, 감축에 대한 근본적인 원인을 MAP(maximum a posteriori estimation) 로 접근하여 규제(penalty) 를 강화함으로써, 보다 안정적인 정보 전달 function을 개발합니다.

insight

• GNN principle and problem definition

graph neural network 를 수식으로 접근함으로써, 정성적인 부분을 정량적으로 이해할 수 있습니다. 수식이 많이 존재하기에 논문을 읽으시며 지루하시거나 힘드실 수 있겠으나, 고진감래 라는 옛말이 있듯이 한 번 보고나시면 시야가 넓어지는 경험을 해보실 수 있을거라 생각됩니다.

Graph attention

그간 유사도(similarity)를 노드간의 내적곱, 코사인 유사도 등을 통해 생성된 값을 기반으로 측정했었습니다. 내적곱 코사인유사도만 보더라도 목적이 다르기 때문에 도출값이 다르곤 하는데요. 이 도출값이 달라지기에, 그때마다 어떤 방식으로 유사도를 측정할지 저희는 정성적인 부분에 의지하여 선택하곤 했습니다. 바로 이 문제 유사도 함수가 휴리스틱하다 라는 문제를 논문 저자는 IRLS의 bound technique 를 통해 해결해보고자 합니다. bound technique 의 핵심인 penality 가 잘 적용되는경우가 있고 잘 적용되지않는경우 역시 존재할텐데요. 그 경우마다의 값또한 table 형식으로 제시해놓았습니다.

Edge uncertainity

핵심 아이디어가 regularization term 이기에 이 규제가 필요한 상황인 high homophily (비슷한 노드는 비슷한 노드들끼리 정보가 전달되기에 발생하는 oversmoothing) 본 아이디어가 잘 적용될 것인가? 즉 heterophily graph , 실세계 그래프 데이터셋들에 대해 과연 이 방식들이 유효할것인가? 라는 의문이 드실텐데요. 그 의문에 대한 답 또한 실험 및 결과 해석까지 나와있습니다. node마다 특성이 다름을 label variant 로 생각하고 그 variant 를 측정하는 지표인 homophily 를 활용해서 low & high homophily 데이터셋에 각각 제안 방법론을 적용합니다.

PRE-TRAINING VIA DENOISING FOR MOLECULAR PROPERTY PREDICTION

https://arxiv.org/pdf/2206.00133.pdf

preliminary

Force field

force field is a mathematical model used to describe the interactions between atoms and molecules in a system. It specifies the energy associated with a particular configuration of the system, based on parameters such as atomic charges, bond lengths, and angles. A force field can be used to calculate the forces acting on each atom in the system, which in turn determine the motion of the atoms over time.

Boltzmann distribution

A Boltzmann distribution ****is a probability distribution that describes the probability of a particle occupying a particular energy state in a system at thermal equilibrium. It is characterized by a single parameter, the temperature of the system, and is given by the formula:

$$ P(E) = (\frac{1}{Z}) * exp(\frac{-E}{kT}) $$

P(E) = (1/Z)*exp(-E/kT)

where P(E) is the probability of occupying an energy state E, Z is the partition function, k is the Boltzmann constant, and T is the temperature of the system. The Boltzmann distribution describes the probability of a particle being in a particular energy state, rather than the probability of a random variable taking on a particular value.

summary

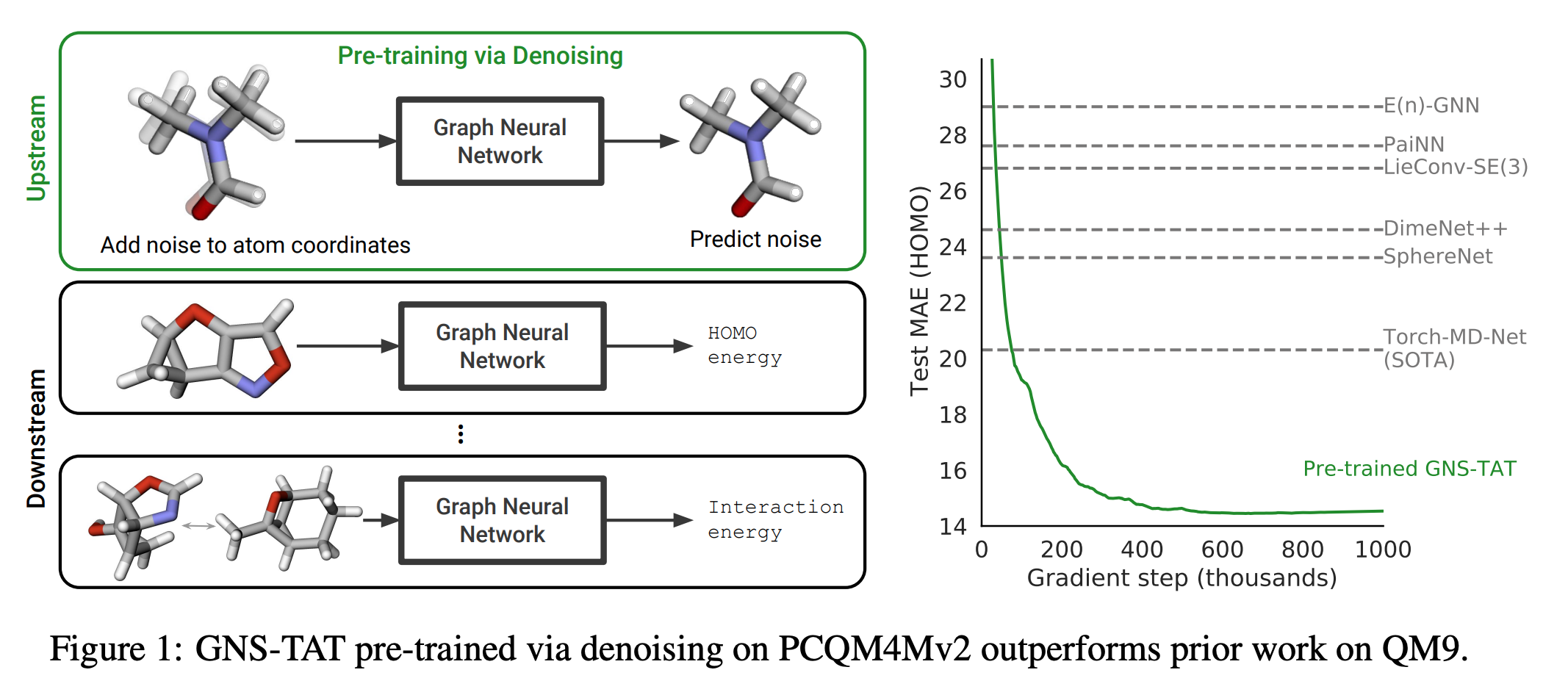
In this paper, the authors used a pre-training technique based on denoising to improve molecular property prediction from 3D structures. They utilized large datasets of 3D molecular structures at equilibrium to learn meaningful representations for downstream tasks. The denoising objective corresponds to learning a molecular force field directly from equilibrium structures. They applied this pre-training technique to the TorchMD-NET architecture, which is a transformer-based architecture that maintains per-atom scalar and vector features updated in each layer using a self-attention mechanism. The authors used gated equivariant blocks applied to the processed scalar and vector features for denoising.

insight

noise handling, 3D coordinate information 을 어떻게 denoise term에 적용할 수 있을지.

boltzman distribution 을 서두에 언급드린 이유는 바로 Energy state라는 term 을 통해 distribution 을 manipulate 할 수 있기 때문인데요. 그 distribution 에 따라 어떻게 denoising 할지에 대한 전략이 본 논문에 나타나 있습니다. 특히, molecular 분야에서는 force-field 측면에서 원자간 결합을 통해 어떤 에너지가 나오는지 원자의 길이, 크기가 어떤지에 따라 그 값이 제각각이기에 이 변동사항을 모두 파악하는게 핵심이라고 볼 수 있는데요. 그 관련 정보와 3D coordinate (X,Y,Z)를 추가하여 변동사항을 좀 더 정밀하게 체크한 후 denoising 한다는 아이디어가 핵심이라고 볼 수 있겠습니다.

Edgedelta , pretraining model handling

“Edge-Delta”, which initializes to zero the weights that multiply incoming vertex features in the edge update functions (and treats these weights as absent for the purpose of computing the initial weight variance).

기존 pretarined model 을 활용하기 위해선 layer parameter 를 freeze 하고 학습시키는 방식인 Fine-tunning 을 애용하고 계셨을텐데요. 모든 영역에서 그 방식이 통용된다면 좋겠으나 , molecular & Graph neural network 에서는 그 방법을 적용하는데에 좋은 성능을 기대하기가 힘듭니다. 그 이유로는 pretraining model 의 과도한 bias (smoothness)가 오히려 molecular discovery 에서 biased 된 결과를 낳을 수 있으니깐요. 그 biased 된 결과를 edgedelta 를 적용해서 weight variance Result 를 얻어냅니다.

A network-based strategy of price correlations for optimal cryptocurrency portfolios

[https://arxiv.org/pdf/2304.02362.pdf]

네트워크 분석과 자산배분전략

[https://www.smallake.kr/wp-content/uploads/2018/07/네트워크-분석과-자산배분전략한국투자증권.pdf]

preliminary

MST(Minimum Spanning Tree)

A Minimum Spanning Tree (MST) is tree-like subgraph of a connected, undirected graph that connects all the vertices of the graph with the minimum possible total edge weight. In other words, it is a subset of the edges of the graph that forms a tree connecting all vertices while minimizing the total weight of the edges.

Summary

가벼울수도 있으나 무거울수도 있는 주제를 가져왔습니다. 바로 ‘돈’ 에 관한 주제인데요. 주식시장 혹은 가상화폐시장에서 correlation 을 통해 포트폴리오 최적화를 진행한 아이디어 입니다. 논문의 골자를 주식시장을 예로들어 설명해보겠습니다. 주식 시장에서 기업의 가치를 평가하기 위한 여러 방식들이 존재합니다. 기업 재무제표만 보고 평가하기에도 벅찬데 해당 기업뿐만아니라, 정치 , 환경 , 내부 리스크 등 다양한 요소들을 고려하여 종합적으로 판단해야하기에 정답이 없는 분야가 기업 가치 측정 분야라고 볼 수 있겠습니다.

이 가치에 영향을 주는 외생/내생 변수들을 모두 측정하기엔 한계가 있으니, 영향을 끼칠만한 변수들만 선별하여 포트폴리오 잘 설계하는게 핵심이라고 볼 수 있습니다. 본 논문들에서는 그 변수들을 각 나라 , 가상화폐 가격 의 correlation 으로 가정하고 각각 네트워크를 설계해줍니다.여기에서 핵심은 각 노드간 연결되어 있는 엣지 가중치(weight) 라고 볼 수 있습니다. MST 의 핵심이 네트워크 내 설정된 weight를 통해 중요한 노드들만 선별해내는것이기 때문이죠

Insight

• MST (minimum spanning tree) 를 통해 실세계 문제를 접근하는 방식.

결국에 핵심은 weight라고 할 수 있습니다. 가중치를 어떻게 설계하고 그 가중치가 과연 타당한지에 대한 사고실험이 중요한 분야라고 할 수 있겠습니다. 또한, NP-hard 문제에도 봉착하게 되는데요. 그 연산량 문제를 해결하기 위해 결국 적합한 네트워크 모델링을 하는게 중요해 보입니다. 본 논문에서는 그 고민들을 어떤식으로 접근하였고, 접근하며 발생한 시행착오 그리고 핵심 결과 도출까지에 대한 내용이 잘 나와있기에 본 방식에 대해 고민이 있으셨던 분들에게 많은 도움이 될 거라 생각되네요.