24년 4월 첫째주 그래프 오마카세

Exploring the Devil in Graph Spectral Domain for 3D Point Cloud Attacks
ECCV 2022
Keywords
Point Cloud Classification, Graph Signal Perturbation, Graph Fourier Transform
Background
- Graph Signal Processing (GSP)을 들어보신 적이 있으신가요? 최근 Graph domain에서 잘 활용되고 있진 않으나 Graph Spectral Theorem으로부터 Graph Convolutional Networks(GCNs)가 파생된 사실을 통하여, 알아두면 나중에 도움이 될 수 있는 중요한 그래프 개념들이 많이 담겨 있습니다.
- 데이터의 Geometric structure를 잘 표현하는 포인트 클라우드를 효율적으로 처리하기 위해서 Graph Topology 정보를 담고 있는 Graph Laplacian Matrix으로 구축되어진 GSP 방법들을 적극 활용해볼 수 있습니다.
- 자연적으로, 각종 Sensors로부터 얻어진 Raw 포인트 클라우드는 device 특성에 따라 수많은 잡음(Noise)이 포함되어있을 수 있습니다. 그리고 대부분의 GCNs은 이러한 잡음에 상당히 취약한 문제점을 드러냅니다.
- 그 이유는 2D image convolution operation과 달리, Graph convolution operation은 흔히 Message Passing으로 불리우는, 이웃의 정보를 "집계"하는 방식으로 동작하기 때문입니다. 직관적으로, 원본 데이터의 잡음은 GCNs에서는 처리되는 것이 아니라 반복적으로 전파되어질 수 있습니다.
- 따라서 Graph Denoising 및 Noise-robustness GNN Design 등의 문제에서는 Spectral domain 상에서 잡음을 처리하고 있으며, 그것이 Data domain에서 보다 더욱 효율적일 수 있습니다.
- 위의 아이디어를 바탕으로, 이번 주 오마카세에는 포인트 클라우드의 잡음에 Robust하면서 정확한 포인트 분류 모델을 설계하기 위해서, Graph Spectral Theorem을 차용하여 좋은 결과를 보여준 꽤 신선하고 재밌는 논문을 가져와보았습니다.
(오늘 오마카세는 약간의 수학적인 개념들이 포함될 수 있을 것 같습니다. 기초적인 선형대수학 개념만 있으시다면 충분히 이해할 수 있을 정도로 어렵진 않을 것 같으니.. 맛있게 즐겨주세요 !)
Introduction
- 자율주행, 의료 이미지 분석 등 다양한 도메인 상에서 널리 활용되고 있는 포인트 클라우드는 취득되어진 Lidar sensor, MRI 등의 Device 속성에 따라 자연스럽게 많은 잡음들이 내재되어있을 수 있습니다.
- 이러한 Noise는 AI 모델 학습에 큰 오류를 일으킬 수 있으며, 위의 Application의 경우 잘못하면 사람 생명에 치명적인 위험을 초래할 수 있기 때문에, 적절한 Noise 처리, Denosing 및 Noise-Robustness model을 설계하는 것은 실질적으로 매우 중요한 문제가 됩니다.
- 본 논문의 저자들은 육안으로 쉽게 관측 가능한 잡음보다, 쉽게 감지할 수 없는 다소 어렵고 치명적인 잡음 신호의 포인트 클라우드를 처리할 수 있는 모델을 설계하고자 하였습니다.
- 다음을 위해, 저자들은 Spectral domain 상에서 original points를 perturbation하는 방법을 통해 adversarial samples를 생성하고, 이들을 다시 data domain 상으로 mapping하여 PointNet & PointNet++, DGCNN 모델을 학습시킵니다. 여기에서 trainable Perturbation 기반으로 잡음을 생성하는 방법론을 본 논문에서 Graph Spectral Domain Attack (GSDA)라고 부릅니다.
Methodology
- 그렇다면 해당 포인트 클라우드 데이터를 어떻게 Spectral domain 상에서 분석하고 처리할 수 있을까요? 이를 위해서, 저자들은 먼저 포인트 클라우드를 잘 표현하는 undirected KNN-graph을 구축한 후, 다음 그래프를 Graph Fourier Transform (GFT)을 통해 Data domain에서 Spectral domain으로 mapping하는 방식을 채택하였습니다.
- 단순하게 GFT는 Time-domain에서의 Fourier Transform을 Graph domain에 적용한 것으로 생각할 수 있습니다. 그렇다면 여기에서 GFT는 어떻게 정의되는 것일까요? 다음을 정의하기 위해서는 일반적으로 (Combinatorial) Graph Laplacian matrix를 활용합니다.
Graph Laplacian Matrix (L)
- (Combinatorial) Graph Laplacian matrix는 쉽게 Graph Degree Matrix (D)와 Adjacency Matrix (A)의 차이를 통해 정의합니다. 따라서 Graph Laplacian matrix는 해당 그래프 노드들의 Centrality 및 Connectivity를 함유하고 있다고 볼 수 있으며, 즉 Graph Topology를 표현하고 있다고 생각해볼 수 있겠습니다.
- 다음 Laplacian matrix는 symmetric하고 positive semi-definite 하기 때문에, 다음 행렬에 Eigendecomposition(고유분해)를 수행할 수 있습니다.
- Decomposition을 통해 얻어진 eigenvector matrix U (고유벡터) 및 eigenvalue matrix \lambda (고유값)에 대해서, Matrix U는 서로 orthonormal한 eigenvector를 Column vector로 포함하고 있으며, Matrix \lambda는 Ascending하게 정렬된 eigenvalue를 대각요소로 가지고 있는 Diagonal Matrix입니다.
- 여기에서 Orthonormal한 성질을 갖는 eigenvector는 Graph spectral space의 basis vector(기저벡터)가 되고, 그에 대응하는 eigenvalue는 Graph Frequency가 됩니다.
- 다음 Matrix U를 통해 Spectral domain으로 원본 포인트 , 명확하게는 해당 포인트의 Feature 혹은 내재하는 Signal, 를 mapping시킵니다. Mapping된 다음 신호 (\hat_x)를 GFT coefficient (계수)라고 칭합니다.
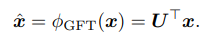
Analysis in Graph Spectral Domain
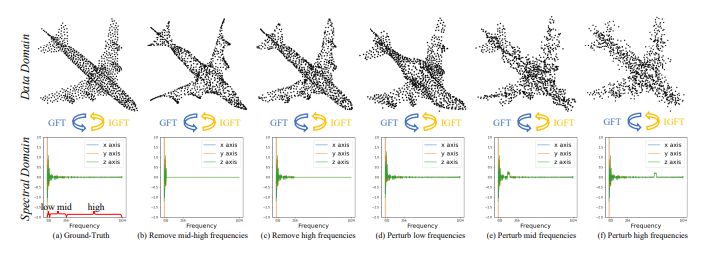
- Fig 2에서, 저자들은 원본 Low & Mid & High-Frequencies의 속성을 확인해보기 위해서, 하나의 Frequency만 남겨두고 나머지 Frequencies들을 제거한 이후 그 결과를 확인합니다. (a~c)
- 또한 저자들은 각각의 Frequencies에 기본적인 Perturbation 방식인 Gaussian Noise를 추가한 결과도 확인합니다. (d~f)
- Fig 2(a)의 Airplane Sample에는 대체로 Low-Frequencies 혹은 smaller eigenvalues 값에 많은 신호들이 분포하고 있으며, Mid & High Frequencies에도 소수의 신호들이 분포해 있음을 확인해볼 수 있습니다.
- Fig 2(b)를 통해, Low-Frequency에는 대체로 Rough shape가 포함되어 있음을 알 수 있습니다. Fig 2(d)에서 다음 Frequency를 perturb시켰을 때, 전체적인 Airplane shape가 뭉개지는 결과를 확인해볼 수 있습니다.
- Fig 2(c)를 통해, High-Frequency에는 fine-grained shape 혹은 Noise가 포함되어 있다는 사실을 확인할 수 있습니다. Fig 2(f)에서 다음 Frequency를 perturb시켰을 때, local detail이 사라지고 noise가 부각되는 결과를 확인해볼 수 있습니다.
- 다음 결과를 통해, 포인트에 내재하는 다른 Frequencies에는 각각에 해당하는 Geometric structure 정보들이 포함되어 있다는 사실을 알 수 있습니다.
- 따라서 저자들은 Frequencies에 적당히 큰 Perturbation을 주입하여 육안으로 해당 잡음을 감지하기 어려운 Adversarial한 포인트 클라우드를 생성합니다. 그리고 Adversarial 포인트 클라우드를 다시 Data domain 상으로 mapping하기 위하여 Inverse Graph Fourier Transform (IGFT)를 수행합니다.

Graph Spectral Domain Attack (GSDA)
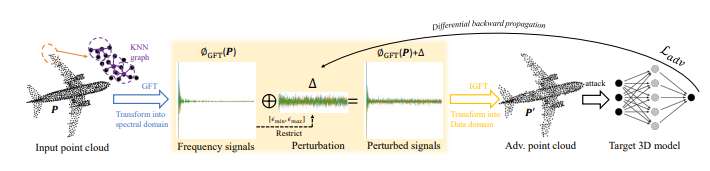
- 저자들은 적절한 Adversarial perturbation (Fig 3의 \delta)를 만들어내기 위해, Learnable한 방식으로 GFT coefficient를 perturbation하고(결과 P`), 이를 Optimization하는 방법으로 학습을 진행하는 GSDA 방법을 제안합니다.
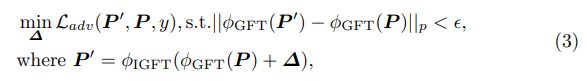
- 식별하기 어려운 결과를 만들어내기 위해, L2-norm(p=2)를 적용하여 perturbed result P`과 original P 사이의 거리를 regularize합니다. 여기에서 \epsilon 파라미터는 해당 distance를 constraint하는 역할을 합니다.
- Perturbation learning은 전체적으로 L_adv loss 함수를 통해 진행되며, 다음 함수를 minimize하는 방향으로 trainable perturbation (\delta)을 업데이트 합니다.
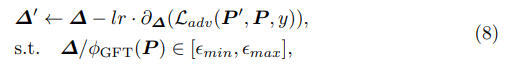
Experiments
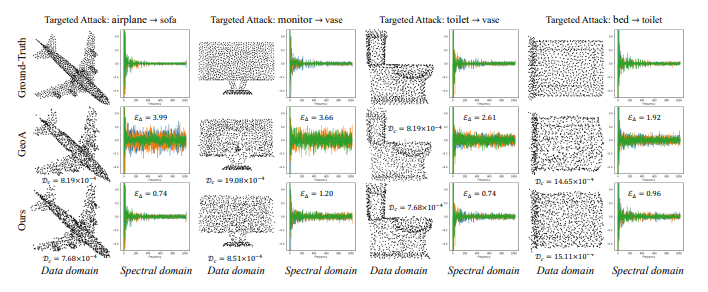
- GSDA를 통해 학습된 Perturbation을 각각의 Frequencies에 주입한 결과를 Fig 4에서 보여주고 있습니다.
- 결과적인 포인트 클라우드의 Geometric structure은 Ground Truth과 크게 다르지 않아 보이지만, 실질적으로 포인트에 내재된 Signal 차이는 매우 크다는 것을 알 수 있습니다.
- Fig 4를 통해 필자가 얻어갔던 인사이트는, Data domain 상에서 Ground Truth와 유사한 Shape를 갖는 Samples들을 잘 구별할 수 있는 확실한 방법은 Spectral domain 상에서 Signal Analysis를 통한 접근방식이 있을 수 있겠다는 것이었습니다.
- 다음 속담이 생각났습니다.
겉만 보고 판단하지 말라 (Don`t judge a book by its cover)
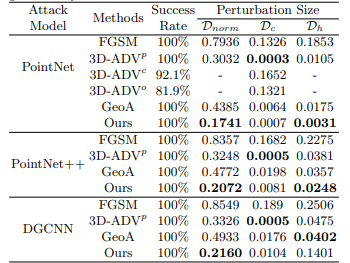
- 저자들은 PointNet, PointNet++, DGCNN의 3가지 pointcloud classification- Baseline 모델들을 대상으로, 여러가지 Attack method들의 Success rate를 비교하였습니다.
- 대부분의 방법들이 100%의 성공률을 달성하였으나, 본 논문에서 제안하는 GSDA는 상대적으로 낮은 Perturbation size만으로도 충분히 높은 결과를 달성할 수 있다는 점이 인상깊었습니다.
- 그 외에도 KNN-graph 구축 시, K 값에 따른 Success rate 및 해당 Perturbation size를 비교한 ablation study 부분도 참고해보시면 좋을 것 같습니다.
Summary
- Noise-robustness한 모델 설계를 위해, Graph Spectral domain 상에서 구축된 KNN-graph의 Low & Mid & High-Frequencies를 trainable한 방식으로 Perturbation하여 Ground Truth에 Adversarial한 Sample을 생성하는 방법으로 본 저자들은 GSDA를 제안하였습니다.
- 그래프 도메인, 구체적으로 Graph Signal Processing (GSP) 관점, 으로부터 소개해드린 이번 논문에서 얻어갈 수 있는 인사이트를 아래와 같이 정리해보았습니다.
- Data domain 상에서는 분별하기 어려운 Geometric difference를 Spectral domain 상에서 Signal analysis를 통해 수행할 수 있다.
- 데이터에 내재하는 Signal의 각 Frequencies마다 기여하는 Properties가 다르다. 다음을 기반으로 여러가지 분석 및 응용이 가능하다는 가능성을 확인할 수 있다.
- 하지만, 해당 그래프는 fixed한 Transductive 방식에 한정적으로 적용이 가능할 것으로 보이며, 널리 사용되는 Inductive 방식에는 어려움이 있을 것 같다. (실제로, Spectral methods은 대부분 Transductive 경향이 존재합니다.)
[Contact Info]
Gmail : jhbae7052@gmail.com / jhbae1184@waseda.akane.jp
Twitter (X): @jhbae1184
Mamba & Graph-Mamba
정이태
오늘 다뤄볼 재료는 GraphMamba입니다. Transformer 대항마로 언급이 되고 있는 아키텍쳐죠. Mamba, 과연 Graph에선 어떻게 Mamba 를 적용하여 성능 향상을 꾀할까요? 논문에선 Graph Transformer 그리고 GraphGPS 까지 언급하며, 각각 아키텍쳐의 한계점과 그리고 GraphMamba 가 개선할 수 있는 부분을 이야기합니다. 또한 실험 그리고 실험 결과를 통해 Mamba아키텍쳐가 Graph 데이터에서도 효과적임을 입증합니다.
GraphMamba에 대해 살펴보기에 앞서 우선, 왜 Mamba 가 회자되고 있는가 부터 짚고 넘어가보도록 하겠습니다. 분야를 가리지 않고 Foundation model 기본 아키텍쳐로 활용되고 인기있는 Transformer, 늘 좋은것을 원하고 개발해야하는 현 세대의 흐름에 따라 자연스레 좀 더 신속하게 좀 더 정확하게 할 수 없을까 라는 의문을 품으며 Mamba 아키텍쳐가 언급되고 있지 않을까 합니다.
Transformer 의 Attention 으로부터 이야기가 시작됩니다. 각 토큰간 중요도를 판별하기 위해 적용하는 Attention, fully-connected 형태로 모든 토큰간 곱을 해주어야 하기에 quadratic 형태의 방정식을 연산해야하고 이 때 많은 자원이 필요하다는 점이 가장 큰 단점으로 언급되곤 합니다.
Attention 에서 연산되는 부분에 대해 문제를 제기하며 이를 linear하게 풀어본다 라는 맥락으로 대두되고 있는게 바로 Mamba이구요. 그럼 과연 Mamba는 어떻게 linear 형태로 이를 해결하려했을까요? 바로 Selective State Space Model (SSM)입니다.
State Space Models(SSM)은 무엇일까요?
ChatGPT4에 따르면 , State Space Model은 시스템의 상태를 설명하기 위해 사용되는 수학적 모델입니다. 이 모델은 특히 동적 시스템의 분석과 제어에 유용하며, 시간에 따라 변화하는 시스템의 상태를 설명하는 상태 변수와 이러한 상태 변수가 시간에 따라 어떻게 변화하는지를 설명하는 방정식으로 구성됩니다.
State Space Model은 선형 시스템뿐만 아니라 비선형 시스템을 모델링하는 데에도 사용될 수 있으며, 시스템의 입력, 출력, 상태를 포함한 전체적인 시스템의 동작을 표현할 수 있습니다.
mamba code : https://github.com/state-spaces/mamba/blob/main/mamba_ssm/modules/mamba_simple.py#L36
시간에 따라 어떻게 변화하는지를 수학적으로 모델링한 SSM, 과연 어느 부분이 구체적으로 Attention 연산을 대체할 수 있을까요?
SSM은 1.정보를 잘 선별하고, 선별된 정보를 2.GPU 친화적으로 연산하는게 핵심이라 할 수 있습니다. 서두에서 언급한 트랜스포머의 quadratic 연산을 linear 연산으로 낮춘 주역입니다.
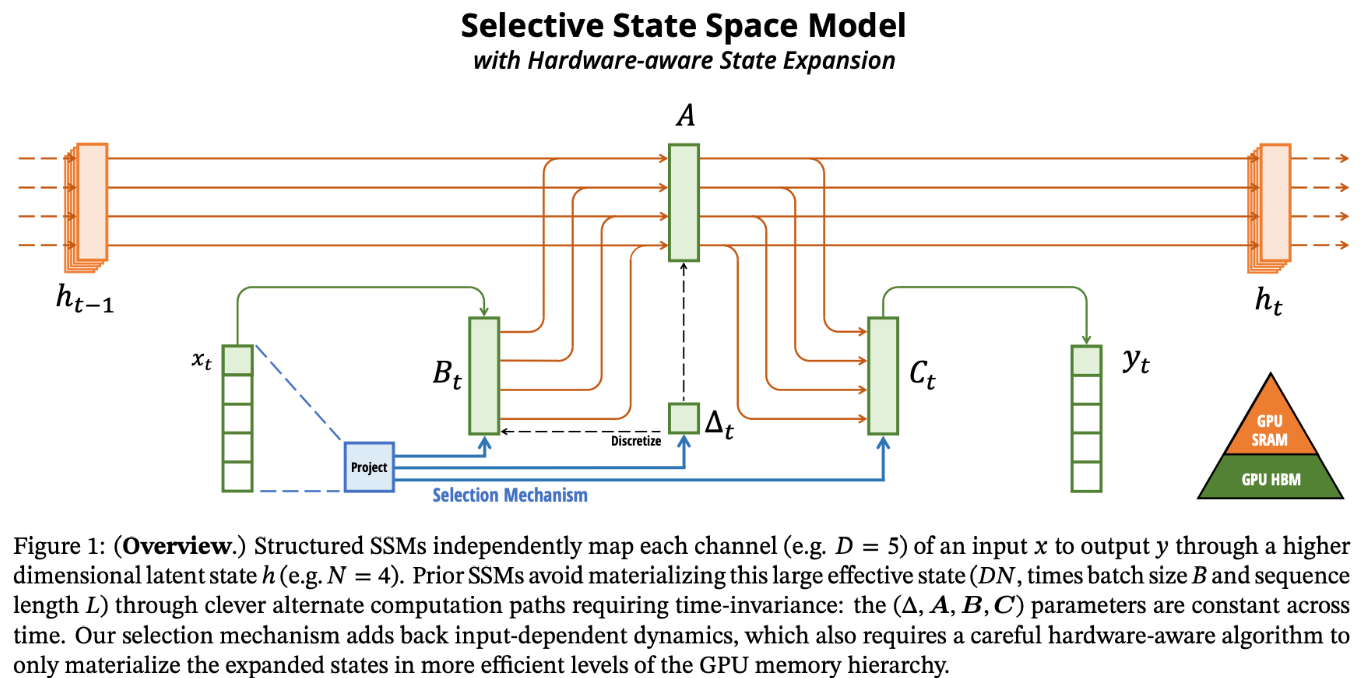
기존 방식은 memory bandwidth boundary 에 대한 제한이 있었는데, 이를 보완하고자 kernel fusion을 활용하여 memory IO 을 줄입니다. 구체적으로는 GPU 내부 데이터 통신 형태를 개선하고자 memory hierarchy 를 활용합니다. 그림1의 우측 하단의 피라미드 모양이 보이실 겁니다. GPU SRAM(Static RAM) , GPU HBM (High Bandwidth Memory) 를 의미하는 그림입니다.
학습을 위한 SSM 파라미터를 GPU HBM 과 GPU SRAM을 번갈아가며 읽어오고 로드하면서 그 연산을 최적화 배분하여 성능향상을 꾀합니다. 구체적으로는 SRAM에서 input을 받아와서 이산화와 recurrence를 해주고, 연산된 값을 HBM 에 전달합니다.
추가로, 중간 상태를 저장하지 않음으로써 메모리 사용량을 줄일 수 있으며, 역전파에서 기울기 계산을 위해 중간 상태를 recomputation 합니다. GPU를 고려한 Mamba의 구현을 통해, GMB는 입력 시퀀스 길이에 대해 선형 시간 복잡도(O(L))를 달성하는데, 이는 트랜스포머에서의 밀집 attention 계산의 제곱 시간 복잡도(O(L^2))보다 상당히 빠릅니다.
본 포스팅에서는 수식 부분을 생략하고, 대략적인 맥락만을 작성했습니다. 그렇기에 추상적인 내용들이 많고 구체성이 다소 낮을수도 있기에 디테일한 Mamba 아키텍쳐를 공부하고 싶으신 분들을 위해 참고하기에 좋은 링크를 가져왔습니다. 하기 3개의 링크 중 하나를 선택하셔서 확인해보시는 것을 추천드립니다.
'''
[원문] Gu, Albert, and Tri Dao. "Mamba: Linear-time sequence modeling with selective state spaces." arXiv preprint arXiv:2312.00752 (2023).
[한글] 모두의 연구소에서 작성한 Mamba 이야기 - https://modulabs.co.kr/blog/introducing-mamba/
[영어] TheGradient에서 작성한 Mamba 이야기 - https://thegradient.pub/mamba-explained/?utm_source=substack&utm_medium=email
'''
Graph-Mamba: Towards Long-Range Graph Sequence Modeling with Selective State Spaces
SSM(State space models) , GPU friendly architecture , transformer alternative , node priority strategy
Paper link : https://arxiv.org/pdf/2402.00789.pdf
graphmamba code : https://github.com/bowang-lab/Graph-Mamba/blob/main/notebooks/mamba.ipynb
타분야와 마찬가지로 그래프에서도 Transformer를 활용하고 있습니다. 그래프에 attention 를 적용하여 결과를 도출하는 graph transformer, 그래프 내 모든 정보를 attention 연산을 하기 때문에 long-range dependency 를 보완할 수 있습니다. 하지만, 모든 정보를 attention 해야하기 때문에 연산량이 상당하며 그래프 분야에서 또한 연산량이 많다는 점을 문제로 제기하곤 합니다.
Graph transformer 아키텍쳐에 MPNN 과 SE(structural Encoding) , PE(positonal Encoding)를 추가한 GraphGPS 또한 논문에서 언급하는데요. 결국 본 논문에서 개선하고자 하는 아키텍쳐가 attention 이고 attention 활용의 끝판왕인 GraphGPS의 attention block 을 GMB(graph mamba block)으로 대체하는게 효과적인가 라는 가설을 입증하는게 핵심이기에, GraphGPS에 대한 언급을 합니다.
아키텍쳐
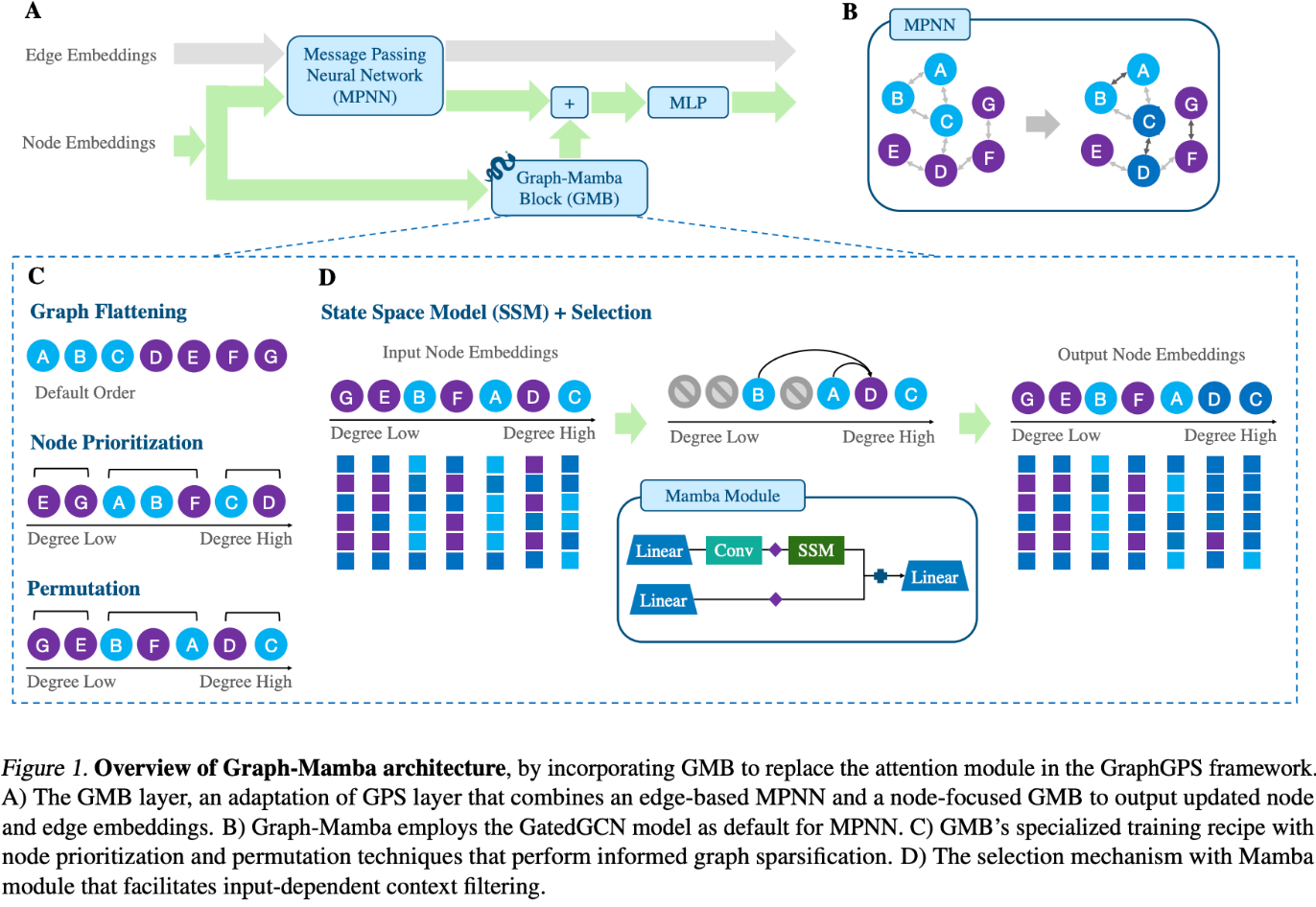
Graph Mamba 도 마찬가지로 SSM를 활용합니다. 하지만, 기존 Mamba 와 다르게 Graph 데이터에 적용한다는 점이 가장 큰 차이점이라 할 수 있습니다.
기존 Selection 알고리즘과 다르게 Graph 에서는 어떻게 Selection을 진행할까요? 바로 Node Prioritization 입니다. 잘 고르고 잘 섞어주는 방식인데요.
flattening 을 통해 recurrence 하게 파라미터가 업데이트 되기 때문에, 순서에 따라 그 노드의 중요도가 다르게 적용됩니다. 그렇기에, 잘고르고 잘섞어주는게 중요하다라고 할 수 있습니다.
논문에 node heuristics that are proxy of node importance 라는 구절이 있습니다. 결국 인풋을 노드 순서 형태로 넣어주어야 하기 때문에, 어떻게 배열을 하는지가 핵심이며 이 배열의 선 후 관계에 따라 전달되는 정보량이 달라지기 때문에 그렇습니다.
Graphmamba 에서는 node importance 를 node hueristic을 활용합니다. node degree가 높은 node가 유의미한 노드일것이다 라는 직관적인 가정하고 진행하는거죠.
이후 heuristic에 따라 잘 골라준 배열을 잘 섞어줍니다. 고생하면서 만들어놓은 잘 골라준걸 왜 섞어주느냐 라는 의문이 들 수 있습니다. 잠깐, 이 모델을 상기해보면 GraphGPS 그리고 그 내부의 attention 을 대체하는게 주 목적인 아키텍쳐입니다. Graph classification 과 Subgraph 정보량을 최적화하는게 핵심 과제라고 할 수 있는데요. 이를 위해 잘 섞어줍니다.
섞어주는 기준은 단순합니다. 그래프 배열 중 node degree(heurstic)이 동일한 노드들에게 noise 를 주어 섞어준다 라고 보시면 됩니다. 이렇게 섞어주는 과정을 N-fold 형태로 반복 적용하여, 그래프 연결에 따라 달라지는 정보를 놓치지않고 임베딩한 결과물을 도출하는게 목적입니다.
지금까지 잘 골라주고 잘 섞어준 input sequences를 GatedGCN 모델에 넣어줍니다. 여기에서 subsequently influencing the current node’s output embeddings. gt ranges between 0 and 1, allowing the model to filter out irrelevant context entirely when needed. 를 하며 관련 있는 정보와 그렇지 않은 정보를 필터링해주게 됩니다. 결국 이 과정이 GraphGPS 의 attention 과 유사하게 정보의 유의미함을 판단하고 적용해주는 역할을 대체하게 된다 라고 보시면 됩니다.
실험 결과
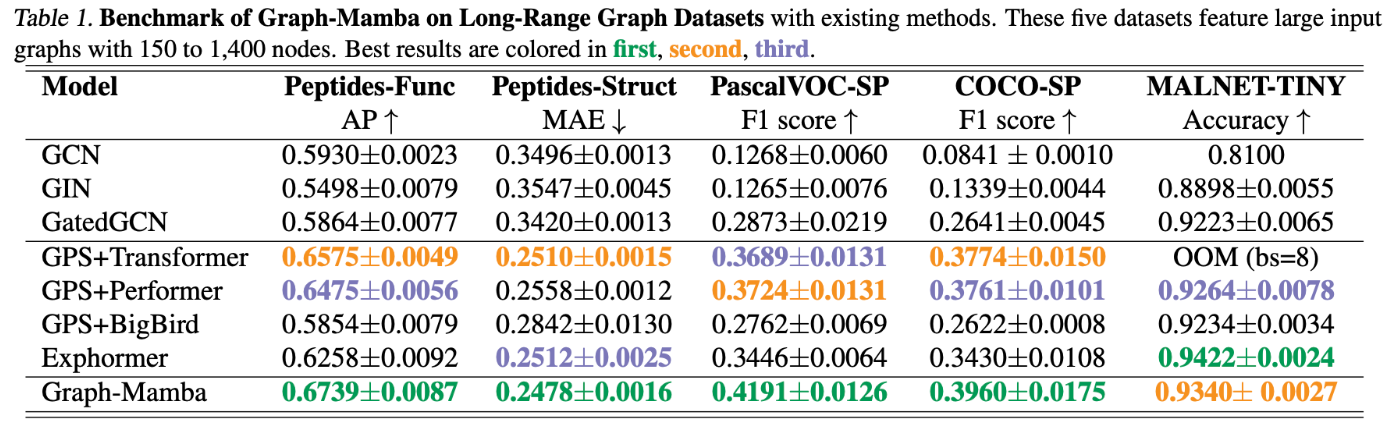
Attention 성능 개선을 꾀한 Performer, BigBird, Exphormer 세 가지 아키텍쳐들을 베이스라인으로 두고 비교한 결과 Graph-Mamba 가 5개의 실험 중 4개의 실험에서 가장 성능이 좋음을 확인할 수 있습니다.
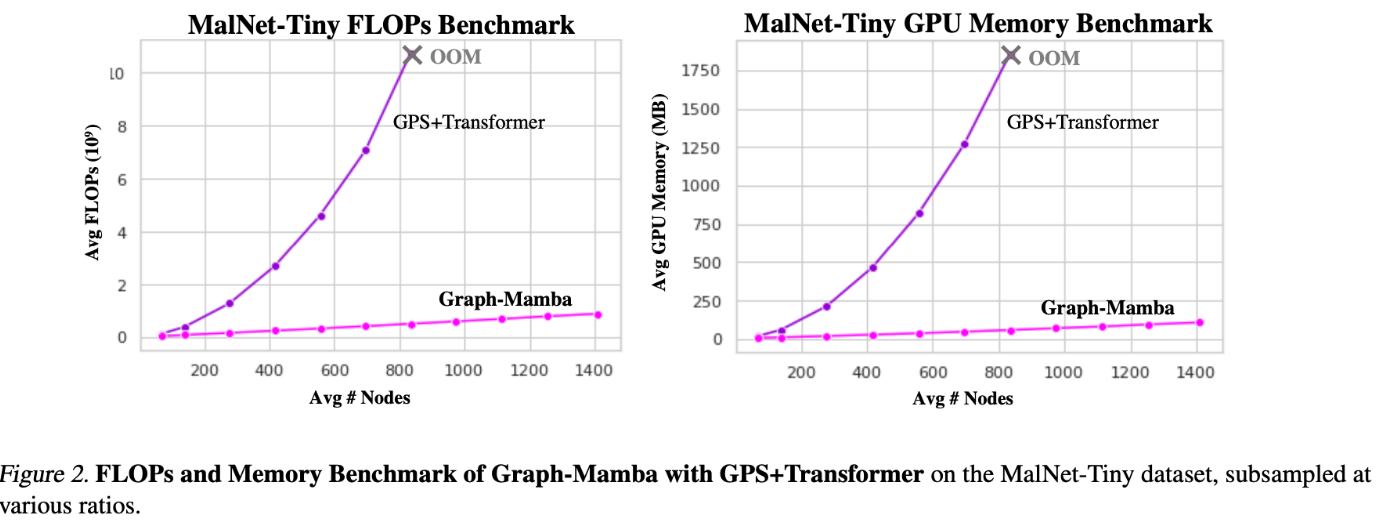
평균 노드가 늘어감에 따라 FLOPs 가 선형적으로 증가하는 Graph-Mamba 대비 GPS+Transformer 는 비선형적으로 증가해 결국 평균 노드 900개 대에서 OOM 이 발생함을 실험 결과에서 확인할 수 있습니다.
요즘같이 foundation model 의 가치가 급증하는 가운데, large data set을 학습하는것 또한 중요한 아키텍쳐 선정 기준이라 생각합니다. 선정 기준을 만족할만한 구미가 당기는 실험 결과이지 않을까 싶네요.
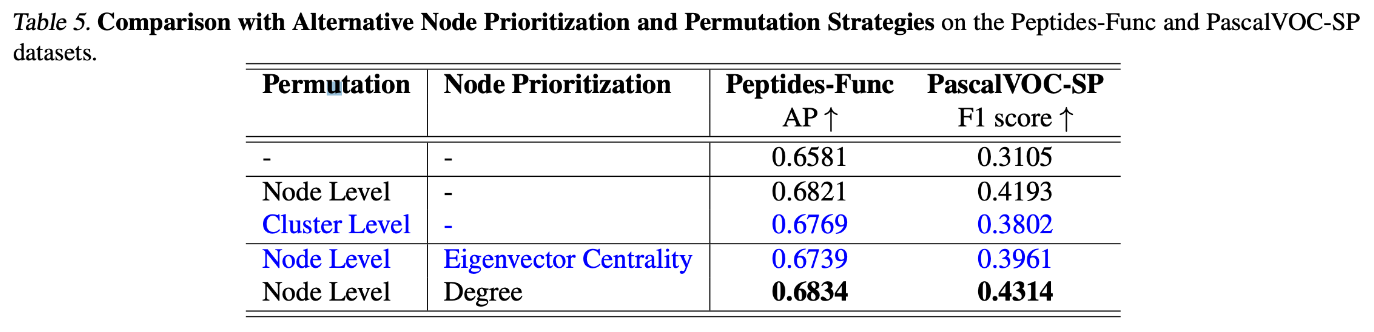
실험 결과 들 중 재밌는 부분은 바로 degree 와 Eigenvector Centrality 를 각각 Node prioritziation (node filtering) 부분에서 작동하였을시, degree 가 더 성능이 높게 나온 부분입니다.
자신의 연결 그리고 해당 그래프에서 자신의 영향력을 연산한 eigenvector centrality 보다 단순하게 edge connection 수를 활용한 degree가 노드 중요도를 판별하는데 유의함을 간접적으로 확인할 수 있습니다. 실험에 활용한 Peptides 혹은 PascalVOC 데이터 특성인 분자나 비디오 측면에서 오히려 부정적일 수 있다 라는 해석을 할 수 있겠네요.
하드웨어 & 소프트웨어 & 수학적 모델링을 연계지은 총 집합체라고 생각합니다. 오마카세 주방장 역시 이 3개를 고루 이해하며, 논문을 읽으려고 하니 잘 읽히고 잘 쓰이지 않더군요. 하지만, 이해한만큼 견식이 넓어지는 좋은 배움이였다 생각합니다. GPU 를 효율적으로 활용하기위해 하드웨어 측면으로 어떻게 접근했고, attention 을 개선하기 위해 recomputation , recurrence 그리고 discretization를 어떻게할지 수학적으로 연산하고 코드로 구현한 부분이 굉장히 재밌었습니다.
[Contact Info]
Gmail : jeongiitae6@gmail.com
Linkedin : https://www.linkedin.com/in/ii-tae-jeong/
