24년 5월 1주차 그래프 오마카세

Diffusion Improves Graph Learning

Neurlips 2019

paper link

official code

Background

• Spatial GNNs의 기본 학습 메커니즘으로 많이 활용되는 Message Passing은 인접 이웃들과의 관계만을 고려하여 중심 노드의 정보를 업데이트 하는 방식으로 진행됩니다.
• 단순한 학습 메커니즘의 유용성과 달리 먼 거리의 노드 정보를 받아 오는 데에는 time costly하고, oversmoothing 등의 여러 문제점들이 존재합니다. 다음 문제들을 해결하기 위한 다양한 방법들이 존재하지만, 저의 오마카세 글에서는 Graph Diffusion Process를 기반으로 접근한 방법들을 다루고 있습니다.
• 이번에 소개해드릴 논문은 Graph Diffusion Learning의 토대를 마련해준, 기초적이면서 해당 토픽에 매우 중요한 내용들을 정리 설명해주고 있어서 작성자의 입장에서 나름 많은 공부를 할 수 있었고 도움이 될 것 같아서 선택해보았습니다.
• 19년도 출판된 논문이나, Graph Diffusion Kernel 및 Neural Networks 설계에 있어서 Base가 되기 때문에, 현 기준 600회 이상 인용되고 있으며 관련 도메인에 관심이 있으신 분들 혹은 공부를 하고자 하시는 분들께 Guide paper로써 추천해드립니다.
• 글의 복잡성을 줄이기 위해, 자세한 어려운 개념 및 설명은 최대한 생략하고자 합니다. 관심이 있으신 독자분들은 꼭 해당 논문을 직접 읽어보시고 많은 인사이트를 얻어가셨으면 좋겠습니다.
• 해당 논문에 대한 좋은 설명을 제공하는 블로그들도 많이 존재하니, 참고해보시는 것도 좋을 것 같습니다.

Introduction

• Spectral Graph Convolution의 강력한 expression power에 비해 not scalable함과 unseen graph에서 갖는 여러가지 한계점들은, 비록 위 방법들보다 강력한 power를 갖진 않지만 scalable하고 여러 도메인에서 extendable or flexible한 특징을 갖는 MPNNs으로 완화될 수 있음을 많은 연구들이 밝혀왔습니다.
• 서로 Trade-off 관계를 갖는 Spectral methods 및 Spatial methods(ex. MPNNs)의 장점들을 모두 활용할 수 있는 방법에는 Diffusion Process을 기본 개념으로 정의해볼 수 있습니다.
• 저번 오마카세에서 언급드렸던 것과 같이 Spatially localized한 Graph convolution을 정의할 수 있을 뿐 아니라 , 기존 GNNs의 레이어 개수에 따라 Discrete하게 이웃 노드들의 정보를 받는 것을 대신하여 시간 t에 따른 Continuous한 Convolution operation 정의가 가능하기에 더욱 넓은 이웃 노드들의 범위를 효과적으로 활용할 수 있다는 장점을 가지고 있습니다.
• 위의 장점을 극대화하여, 기존 Graph Convolution의 메커니즘을 대체하고 더욱 효율적인 GNNs을 정의하는 방법에 대해 소개한 논문으로 생각해볼 수 있겠습니다.
• Graph Diffusion Convolution (GDC) 모듈을 기반으로 설계되는 Graph Diffusion Neural Networks는 powerful, general하면서 Message passing의 대체 Spatial localized한 메커니즘을 모두 차용할 수 있다는 큰 장점을 갖습니다. 또한 다음 GDC 모듈은 여러 GNNs의 학습 메커니즘에 Plug-in 할 수 있다는 점에서 활용성이 매우 높은 장점도 갖습니다.
• Diffusion Process 과정이 Message Passing과 매우 유사하면서도 이를 Generalization할 수 있다는 사실을 기반으로, 위의 Contribution을 이해해볼 수 있을 것 같습니다.

Methodology

• 다음 GDC를 정의하기 위해서, 본 논문의 저자들은 Personalized Page Rank (줄여서 "PPR", 'The pagerank citation ranking: Bringing order to the web. Report', 1998)라는 개념을 활용합니다.
• PPR은 Graph Diffusion Process의 정의에서 coefficient parameter \theta를 정의하는 데 주요한 역할을 갖기 때문에, 해당 개념을 알고 계시면 다음 논문의 설명이 어렵게 느껴지진 않을 것 같습니다.
• Diffusion Matrix (T)를 기반으로 정의한 generalized Graph diffusion process는 식 (1)과 같이 정의합니다.

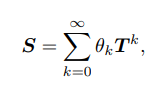
여기에서 Diffusion Matrix (T)는 RandomWalk Transition Matrix T_rw = A * D^(-1/2)로 설정하고, 다음 coefficient \theta는 Teleport prob \alpha를 기반으로 아래와 같이 정의합니다.

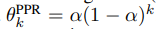
PPR 계수를 도출하는 방법에 대해서는 해당 PPR 논문 혹은 아래 블로그를 참고해주시기 바랍니다.

Python, Machine & Deep Learning

Python, Machine Learning & Deep Learning

• 식 1로 정의한 Generalized Graph Diffusion Matrix (S)로 해당 그래프 G의 Adjacency Matrix(A)를 대체하여 GDC을 정의합니다. 다음 convolution은 Directed Weight Graph에서 활용할 수 있으나, S를 Sparcify하여 해당 weight를 무시하여도 Convolution operation이 잘 동작함을 발견합니다. 즉, 어떠한 그래프 종류에 상관없이 agnoistic하게 GDC 모듈을 활용할 수 있다는 장점을 갖습니다.
• 또한, Graph Diffusion 과정을 통해 이미지에서의 Gaussian Filter와 같이 주변 노드의 정보를 smooth out할 수 있다는 사실, 즉 Graph Denoising 효과를 얻어낼 수 있음(으),로부터 Noisy graph 에서도 Meaningful한 이웃 노드들을 recover할 수 있다는 장점도 언급합니다.
• Generalized Graph Diffusion Matrix (S)를 Sparcification 하는 방법으로 Top-k 혹은 threshold 값을 활용할 수 있으며, 해당 논문에서는 Threshold를 지정하여 그 미만의 값들을 0으로 만들어줌으로써 해당 작업을 수행합니다. 그로부터 S -> \tilde_S를 얻어냅니다.
• 위 Sparcified Matrix S (\tilde_S)를 통해 Transition Matrix T_sym를 아래와 같이 재정의합니다.

• 위 Transition Matrix (T_sym)을 식 1에 대입하여 GDC를 정의하며, 위의 모든 과정을 한 눈에 알아볼 수 있도록 Fig 1에 표현하였습니다.

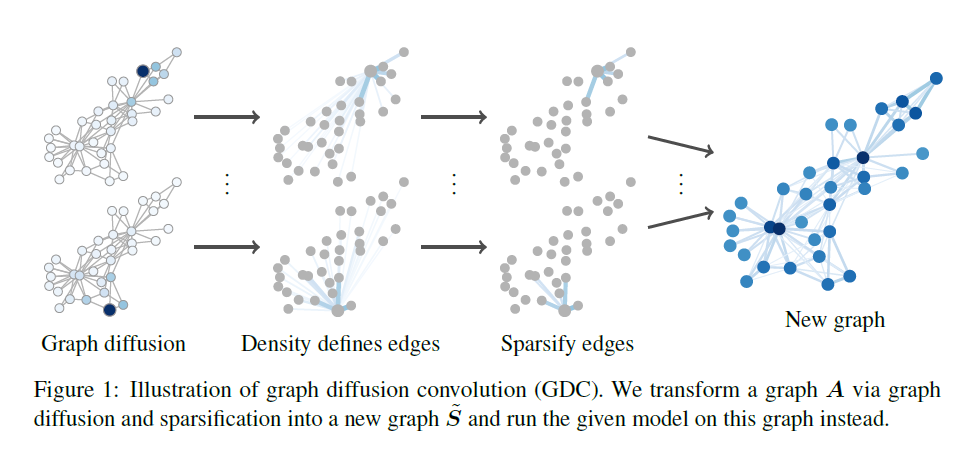
• Fig 1을 기반으로 GDC의 과정을 정리해보면,
  • 해당 그래프의 중심 노드를 기준으로 Message를 넓은 이웃 범위 노드들에 Diffuse한다.
  • 다음 Diffusion은 식 1의 S Matrix로 정의할 수 있으나, Dense Matrix S를 일정 Threshold 값을 통해 Sparcification할 수 있다.
  • Sparcified S의 행렬로 Transition Matrix를 재정의하여, 최종적인 Graph Diffusion Convolution을 통해 새로운 그래프를 얻어낸다.
• 하지만 다음 GDC는 주어진 그래프가 Homophily하다는 가정으로부터 정의되어지기 때문에, Heterophily한 그래프의 경우 효과적인 성능을 달성하기 어렵다고 저자들은 언급합니다.
• GDC 정의에 대한 Spectral Analysis를 위해, 이전 방법들과 동일하게 Graph Spectral Convolution의 식 (2)로부터 식 (3)의 Polynomial filter를 정의합니다.

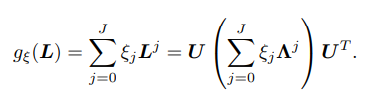
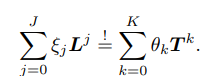
여기에서 Laplacian Matrix L = I_n - T로 설정하여, 해당 coefficient ξ_j, θ_k를 찾아냅니다.

• 자세한 Spectral Properties (Transition Matrix, Summation over T^k, Sparcification ..)은 생략하겠습니다.

Experiments

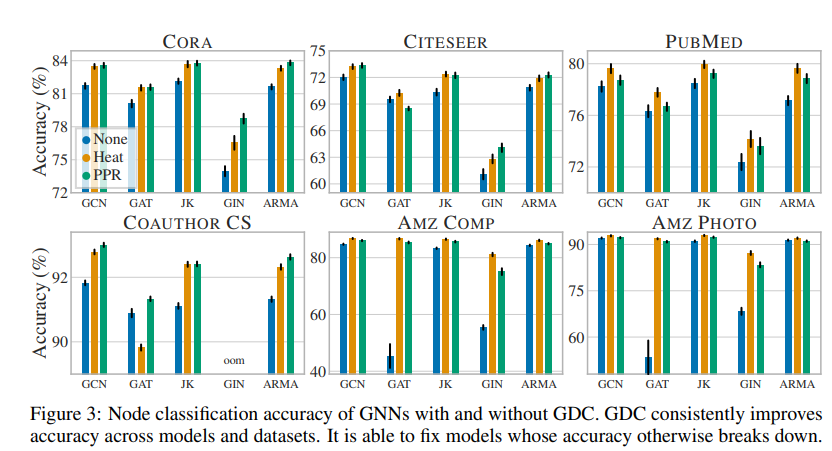
• Fig 3의 Node Classification에서 GDC 성능 확인의 목표는 기존 MPNNs baseline의 정확도 성능을 향상시키는 것에 두고 있으며, 결과적으로 위의 목표를 만족하는 결과를 보여줍니다.

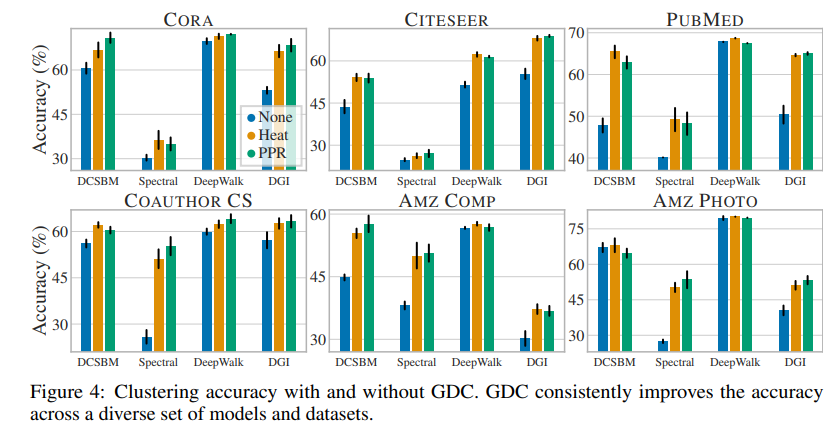
• Fig 4의 Unsupervised Clustering Accuracy에서도 다른 Clustering models (DCSBM, DeewWalk ..)들에 Plug-in한 결과에서 대체로 좋은 결과를 보여주고 있습니다.

Conclusion

• 다음 논문은 기존 Spectral 및 Spatial methods의 Spatially localized하고 Powerful한 장점들을 취하면서, 다양한 기존 MPNNs의 학습 메커니즘에 쉽게 Plug-in할 수 있는 Graph Diffusion Convolution (GDC) 모듈을 제안하였습니다.
• 비록 Homophily한 graph에서 성능이 보장된다는 limitation이 존재하지만, Personalized PageRank 기반 Learnable params (\theta) 및 Sparcified Graph Diffusion Matrix (S)의 적은 파라미터를 통한 단순한 정의로 구현된 GDC 모듈의 좋은 성능을 다양한 실험을 통해 확인해볼 수 있었습니다.
• Message Passing 메커니즘을 Graph Diffusion process로 Generalization할 수 있다는 점에서, 새롭고 효율적인 GNNs 대체 모듈 및 네트워크 설계 도메인에 있어서 관심이 여전히 존재하고 있습니다. 그런 면에서 해당 논문은 새로운 아이디어 및 인사이트를 주기에 충분하다고 생각합니다.
• 해당 모듈은 GNN library인 Torch-geometric 에서도 좋은 설명과 적용 예시를 잘 보여주고 있기에, 해당 docs를 같이 참고해보시는 것도 좋을 것 같습니다.

[Contact Info]

Gmail : jhbae7052@gmail.com / jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn