Graph Convolutional Networks using Heat Kernel for Semi-supervised Learning

배지훈

IJCAI 2020

link : https://arxiv.org/abs/2007.16002

code : https://github.com/Eilene/GraphHeat

Background

• 그래프 컨볼루션의 정의를 한번 다시금 생각해봅시다. 그래프 신호 처리(Graph Signal Processing, GSP)에서 파생된 그래프 컨볼루션은 해당 그래프의 Laplacian matrix를 고유분해하여 얻어진 고유벡터 및 고유값 행렬을 기반으로 연산됩니다.
• 구체적으로 고유벡터 행렬을 통해 입력 신호 x를 Spectral domain 상으로 projection 시킨 후, Localization을 위해 최대 K차수의 다항식 꼴로 표현된 고유값 행렬과 학습 가능한 파라미터의 내적 연산을 통해 컨볼루션 연산이 진행됩니다.
• Spectral Graph convolution model로 유명한 ChebyNet (Defferrard et al.)은 Chebyshev Polynomial 기반의 Convolution Filter를 설계하여 재귀적으로 최대 K hop 떨어진 이웃의 정보를 집계합니다.
• ChebyNet의 높은 연산량 문제를 해결하기 위해 제안된 GCN (Kipf et al.)은 1차 근사 다항식으로 단순화시켰으며, 이로부터 발생하기 쉬운 oversmoothing 문제 완화를 위한 Tricks (ex. adding self-loop)을 통해 현대 그래프 컨볼루션 네트워크의 기반을 마련해주었습니다.
• 그래프 학습에서 중요한 유사도 (Similarity)의 관점에서 다음 컨볼루션 연산은 두 신호의 변동(Variation)이 적은 두 노드에 대한 Smoothness함으로 정의할 수 있으며, 다음 요소는 Graph Laplacian Matrix의 Quadratic form을 통해 고유값 속에 내재되어있음을 알 수 있습니다. 즉, 작은 고유값에 대응되는 노드는 그래프 학습에 있어서 중요한 Anchor라고 바라볼 수 있습니다. 그 반대로 큰 고유값에 대응되는 노드는 일종의 Noise라고 볼 수 있습니다.
• 따라서 Graph smoothing & Denosing과 같은 Applications에서는 그래프의 저주파수만 추출하여 활용하기 위한 Low-Pass Filter 설계가 핵심이며, 가장 널리 사용되어지는 Low-Pass Filter는 오늘 오마카세로 소개해드릴 Heat Kernel입니다.

Introduction

• ChebyNet, GCN의 두 Baseline 모델의 컨볼루션 정의를 자세히 들여다보면,
  • 두 모델의 Convolution Filter는 공통적으로 Graph Laplacian Matrix의 K차수 고유값 다항식을 기반으로 하고 있습니다. 여기에서 GCN의 경우 K=1입니다.
  • 즉, ChebyNet의 컨볼루션은 저주파 요소들로부터 최대 K번 노드의 신호들을 재귀적으로 집계하는 과정을 기반으로 정의되었으며, GCN은 단순히 1번만 모든 신호들을 집계하는 방식의 컨볼루션을 정의하였음을 이해할 수 있습니다.
  • 여기에서 고유값은 오름차순으로 정렬되어지기 때문에 작은 고유값에 대응되는 노드 신호는 저주파 요소가, 큰 고유값에 대응되는 노드의 신호는 고주파 요소가 많이 내재되어있음을 알 수 있습니다.
• Background의 설명을 통해 다음 사실은 ChebyNet은 충분히 큰 K 값을 갖는다고 가정한다면, 해당 그래프의 저주파 & 고주파 요소들을 추출해낼 수 있습니다. 즉 Low & High-pass filter의 성질을 모두 가지고 있습니다.
• 또한 GCN도 모든 노드의 신호들을 추출할 수 있기 때문에 Low & High-Pass Filter로써 동작한다는 것을 알 수 있습니다.
• 다음 논문에서는 대표적인 Low-pass filter로 동작하는 Heat Kernel을 다음 Baseline 모델에 통합하는 방법론을 설명합니다. 그리고 Heat Kernel 기반 그래프 컨볼루션 연산으로 학습되는 네트워크인 GraphHeat을 제안합니다.

Related Works

Spectral CNN : Pioneer of definition of graph convolution

• Bruna et al.은 식 2와 같이 초기 Graph Convolution Filter, g_theta을 괄호 안의 \SUM_n {theta_n * u_n * u_n^T} 형태로 정의하였습니다.

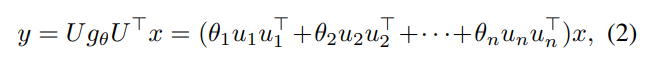
• 하지만 다음 Filter는 learnable parameter가 존재하지 않기 때문에, 새로운 구조의 그래프로 확장시켜 적용할 수 없다는 한계점이 존재합니다.

ChebyNet : Fast Localized Graph Spectral

• Learnable Parameter를 추가하고, 다음 Filter를 Localized하여 연산 속도를 향상시키기 위해, ChebyNet은 다음과 같은 Chebyshev Polynomial Filter를 설계하였습니다.

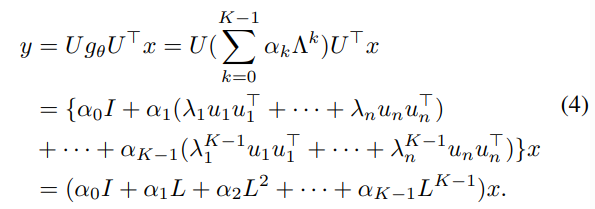
• Learnable Parameter \alpha를 추가하고, Weight parameter로 고유값을 활용하여 최대 K-hop 정보를 재귀적으로 집계하는 방식으로 설계된 ChebyNet은 빠른 학습 수렴속도와 Localizable한 특성으로 많은 연구에서의 Baseline model로써 활용되고 있습니다.
• 하지만 Graph Laplacian Matrix의 거듭제곱 꼴 Convolution process의 과도한 연산량을 요구하는 단점이 존재합니다.

GCN : Approximation to Graph Convolution by 1st Polynomial Filter

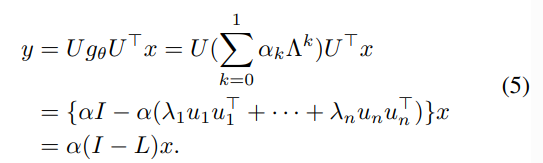
• K번의 집계 과정을 1번으로 간소화시킨 GCN은 고질적인 Oversmoothing 문제를 회피하면서 효율적인 Optimization을 위한 self-loop 추가, Normalized Adjacency matrix 등의 Tricks을 추가하였습니다.

Methodology

• 저자들은 ChebyNet, GCN의 효과적인 Low-pass filter 설계를 통해, 고주파수 요소들을 제거함으로써 해당 그래프 전체를 Smooth하게 만들어주는 GraphHeat 모델을 제안합니다.
• GraphHeat의 Convolution Filter는 식 4, 5에서 큰 고유값에 대응하는 {u_n * u_n^T}가 고주파 요소를 포함하고 있다는 사실을 바탕으로, exp(-L) 꼴로 정의되는 Heat Kernel을 활용하여 고주파 요소들을 0에 가깝게 만들어서 저주파 요소들을 더욱 강조합니다.

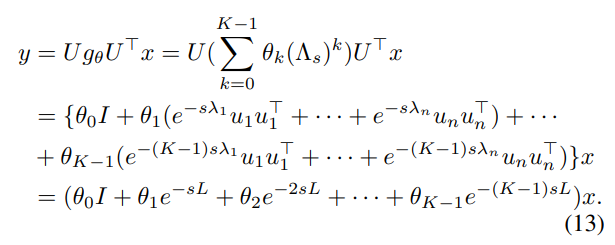
• 식 13에서 \theta_k는 Learnable parameter, s는 Heat diffusion의 rate를 조절하는 scale parameter입니다.

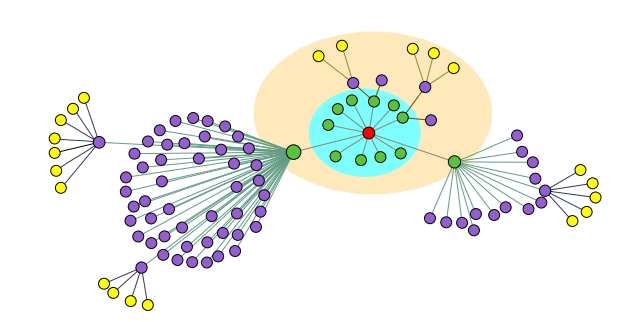
• Transductive하게 그래프 전체의 노드들을 고려하여 shortest-path distance의 노드 신호들을 차례대로 집계하는 ChebyNet, GCN의 동작 방식과 달리, GraphHeat는 Heat diffusion 현상을 따라 Target node인 빨간색 노드에서부터 Similarity가 높은 (즉, 노드 간 신호 차이가 작음) 주변 노드들을 차례대로 집계합니다.
• 한마디로, 이웃 노드를 정의하는 방식이 기존 Baseline model과 GraphHeat의 차이점이라고 볼 수 있겠습니다.

Experiments

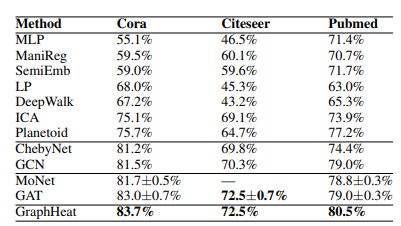
• 3가지 벤치마크 데이터셋 Cora, Citeseer, Pubmed에서 node classification 결과를 나타내었습니다.
• 정량적 평가에서 Baseline model의 Spectral Graph Convolutional networks - ChebyNet, GCN 뿐만 아니라, Spatial Graph Convolutional networks - MoNet, GAT의 성능을 능가할 수 있음을 보여주고 있습니다.
• 해당 데이터셋 특성 상, 해당 그래프 주변 노드에는 유사도가 높은 이웃이 분포하고 있을 확률이 높기 때문에 상대적으로 Smoothness가 높습니다. 따라서 Low-pass filter를 사용하여 그래프의 smoothness를 잘 학습한 모델일 수록, Accuracy가 높게 나올 수 있을 것이라는 가정이 잘 들어맞았음을 알 수 있습니다.

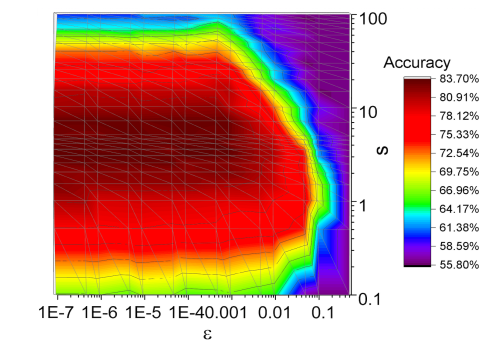
• Fig 4는 Heat kernel의 scale parameter s와 similarity threshold \epsilon 값에 따른 Accuracy 분포의 변화를 보여주고 있습니다.
• s 파라미터가 클 수록, \epsilon 파라미터가 작을수록 상대적으로 더 높은 Accuracy를 보여주고 있으며, 다음은 해당 그래프 상에서 넓은 spectrum 내 더욱 similar한 노드들을 많이 발견해낼 수록 GraphHeat의 성능이 향상되어진다는 사실을 알 수 있습니다.

Summary

• GraphHeat는 이웃 노드와의 Similarity가 높은 데이터셋 상에서 Low-pass filter를 활용하여 다음 Similarity를 잘 포착해내기 위한 Heat Kernel을 기존 Spectral Graph Convolutional networks - ChebyNet, GCN에 통합시켜 더 좋은 성능을 달성하였음을 보여주었습니다.
• Inductive bias에 부합한 그래프의 properties를 잘 활용할 수 있는 방법 및 네트워크라고 생각되었으며, Spectral Graph Convolution을 처음 접하는 독자들에겐 다소 어려울 수 있는 개념을 쉽게 풀어 설명해주어서 읽는 데 큰 어려움이 없었습니다.
• 하지만, 다음 방식은 Spectral domain 상에서 동작하는 Network이기 때문에 Transductive learning 한정 좋은 성능을 보여줄 수 있습니다. 실험에서 사용하였던 데이터셋 역시 Transductive가 강한 그래프로 구성되어있습니다.
• 즉, inductive한 특성이 높은 Real world dataset에서의 learning은 GraphHeat의 한계가 존재할 것으로 생각됩니다. Fixed shape를 갖는 이미지 위에서 구축되어진 그래프에서는 그래도 픽셀 간 중요 특징을 추출하는 모듈로써 활용하는 데에는 괜찮은 방법이 될 것으로 생각합니다.

[Contact Info]

Gmail : jhbae7052@gmail.com / jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn

———

REASONING ON GRAPHS: FAITHFUL AND INTER- PRETABLE LARGE LANGUAGE MODEL REASONING

Paperlink : https://arxiv.org/abs/2310.01061

Codelink : https://github.com/RManLuo/reasoning-on-graphs

정이태

서론

• lack of knowledge , hallucination 두 가지 현상을 완화하기 위해 다양한 시도들을 하고 있는 요즘입니다. 오늘은 여러 방법들 중 Knowledge graph를 활용하는 방법론을 주제로 이야기합니다.
• Knowledge graph, 그래프 내에 엔티티 간 semantic(의미론) 정보를 담아주는 데이터 표현 방식입니다. symbolic AI라는 컨셉에 부합하는 방법론으로써 모든 사물에 대한 이해를 엔티티 & 시멘틱 으로 이해할 수 있다 라는 측면으로 자주 언급되곤 합니다.
• 딥러닝 모델가 현상을 ‘이해’할 수 있다는 점이 오늘 논문의제핵심 키워드 입니다. 그 이해할 수 있는 재료로써 지식그래프를 활용하는 거죠. 그래프 분야에서는 Knowledge Graph Reasoning , KGQA 분야에 속해 있습니다.
• LLM들 lack of knowledge 그리고 hallucination 현상이 발생하는걸까요? 논문 저자는 reasoning process 에서 에러가 발생한게 그 주 원인이라고 이야기하며, Knowledge graph를 이야기합니다. 특히나, legal judgement(재판) 그리고 medical diagnosis(의학진단) 과 같은 판단 한 번에 리스크가 큰 분야에서 에러가 발생한다면 상상하기조차 어렵네요.
• “faithful and interpretable reasoning” 지식그래프를 활용할 시 얻게되는 두 이점을 나타낸 키워드라고 할 수 있습니다. 정말 답변에 참고한 데이터가 있는지, 그리고 그 데이터가 어떻게 형성되어 있는지를 그래프 형태로 직관적으로 볼 수 있다 라는 점이 두 키워드에 함더되어 있습니다.
• 본 논문은 여러 방법론들(Knowledge gRaph Question Answering, KGQA) 중 Knowledge Graph에서 어떤 그래프 정보를 가져오고 , 그 그래프 정보가 과연 질문 그리고 답변에 부합한지 최적화하는 과정을 담았습니다.

방법론 개요

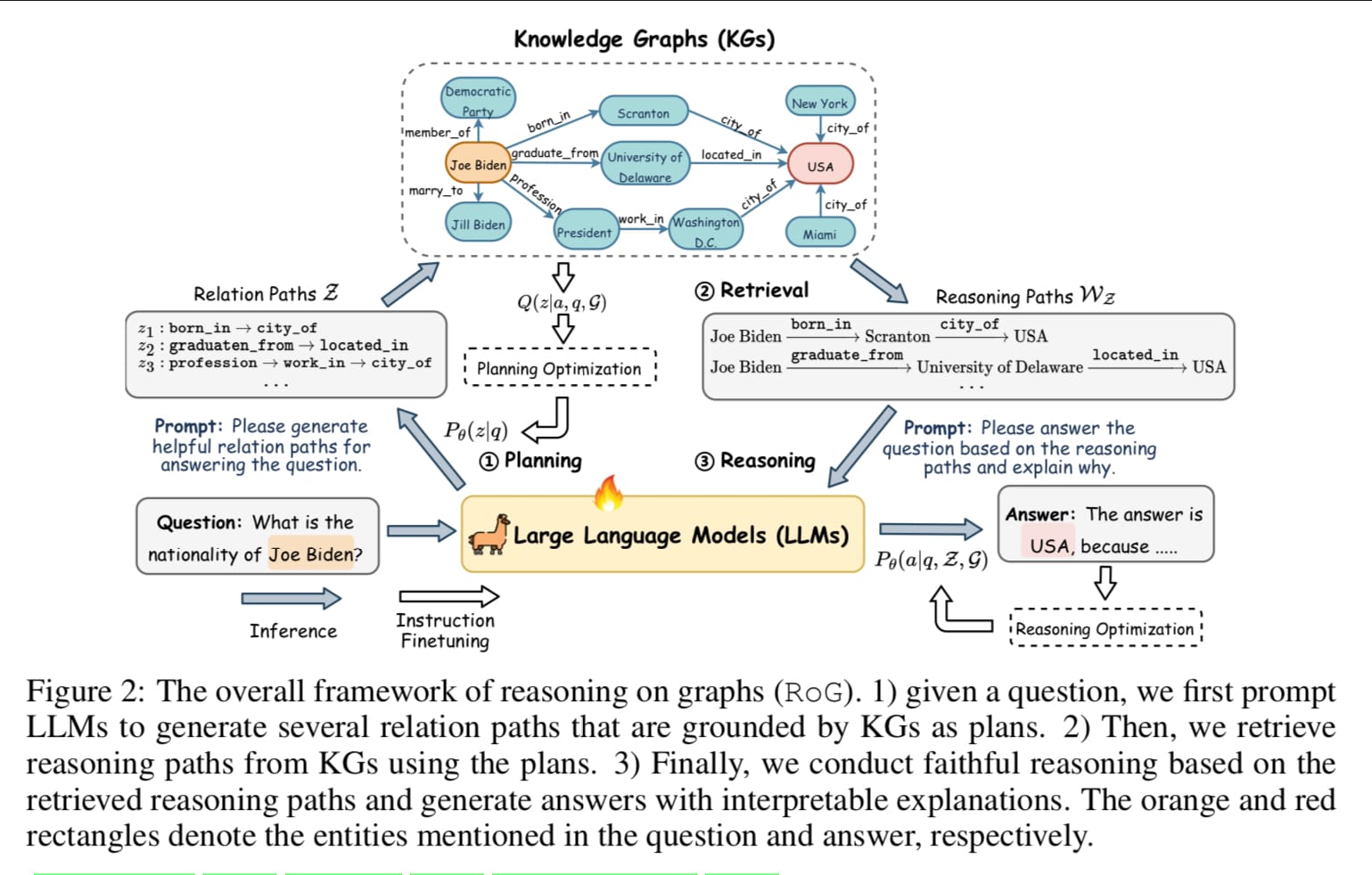
• 방법론은 간단합니다. 잘 가져오고, 가져온것이 최적인가를 검증한 뒤 검증된 Path 를 LLM에게 전달하는 것 이 방법론 핵심입니다. 이를 위해 ELBO(evidence lower bound) 를 활용해 planning 로 생성된 relation path와 retrieval-reasoning 로 생성된 reasoning path 간의 정보량을 계산해 그 간극을 최소화하는 방식으로 최적화가 이루어집니다.
• 이 때, 최적화의 대상은 LLM의 parameter입니다. 다시 말해서, 무엇을 가져오고 가져온 것을 기반으로 답을 만들 때 적합한지를 지속적으로 개선한다는 것이 본 아키텍쳐의 핵심이라 할 수 있습니다.
• 방금 말한 방법론은 크게 3가지 모듈로 나누어집니다. 1. Planning , 2. Retrieval , 3. Reasoning 각각 무엇을 가져올지 계획하는 단계 , 실제 그 무엇을 가져오는 단계 그리고 가져온 것을 Reasoning 형태로 LLM에게 제공하는 단계입니다.
• Planning optimization
  • planning은 relation Paths를 가져오는 KG(knowledge graph) 로부터 추출할 때 무엇이 좋을지 계획하는 단계입니다. 유저의 질문을 기반으로 답변에 도움이 될만한 요소를 Knowledge graph 에서 추출합니다. 논문에서 “distill knowledge from KGs” 라고 표현할 만큼 최적의 결과 값을 뽑아내는게 핵심입니다.
  • 최적화 기준은 question 으로 부터 생성한 realtion path와 실제 path 가 answer 가 relation path와 연결되었는지를 Kullback–Leibler divergence(KLD , 쿨랙라이블러 발산) 을 활용하여 비교합니다. 간단히 말해서, 두 path 간 확률 분포 차를 계산하고 이를 최적화한다 라고 보시면 되겠습니다.
  • 이 때, 확률 분포를 계산할 때 우선 정규 분포를 가정하고 question 과 상응하는 answer이 서브그래프 내 존재할 시 이를 반영하는 방식으로 진행됩니다. 값은 shortest path 의 역수를 반영합니다.
• Retrieval-reasoning optimization
  • Retrieval-reasoning은 planning 으로부터 생성된 여러 path 들 중 무슨 path 가 과연 의미할지를 연산하는 단계입니다. FiD 프레임워크를 활용합니다. FiD 프레임워크란 Fusion-in-Decoder (FiD)의 약자입니다.
  • 다양한 passage 를 독립적으로 인코딩하고, 디코딩시에 독립적으로 인코딩 된 passage 값을 fusion 하기 위한 방법론으로써, planning 에서 생성된 여러개의 faithful relation 을 활용하기 위해 FiD 아이디어를 차용합니다.

** facebookresearch FiD implementation code : https://github.com/facebookresearch/FiD

———

• 서두에 언급드렸다시피, 본 논문의 목적은 LLM의 파라미터를 학습하는게 목적입니다. 지금까지는 지식그래프에서 어떻게 가져오고 어떻게 주입하는지를 이야기했다면, 다음부터는 구체적으로 어떤 input형태로 LLM에게 주입되어 학습되는지에 대해 이야기합니다.
• planning module
  • Planning 은 relation path가 유의미한지를 LLM에게 토큰 형태로 주입해 학습하는 단계입니다. LLM 최적화를 위해 , relation 을 토큰 단위로 분절합니다. path / sep / path 3가지 토큰을 활용합니다.
  • <path> r1 <sep> r2 <sep> … <sep> ri </path> 형태로 주입되며 특정 path 마다 어떤 relation 이 담겨있는지를 토큰형태로 LLM에게 주입하고 이를 파라미터 최적화에 활용합니다.
• Retrieval - Reasoning module
  • 주어진 질문 그리고 relation path 를 활용해 사전에 형성되어 있는 Knowledge graph로 부터 가져오고, 이를 종합해 reasoning paths 그리고 질문 으로 가공하여 LLM에게 주입합니다. 이 때, reasoning paths 의 여러 path들 중 어느 path가 중요한지를 판별하기 위해 reasoning module을 활용합니다.
  • Reasoning module 은 path 결과물마다 answer 값이 정확한지 부정확한지를 확률 형태로 추출한 뒤 이를 기반으로 중요도를 판별하는 역할을 합니다.

실험

• Embedding , Retrieval , Semantic Parsing , LLMs , LLMs+KGs 총 5가지 방법론들을 활용해 실험합니다. 기초 방식 Semantic Parsing 부터 최신 방식 LLMs+KGs 까지 모두 담아놓았습니다.
• Backbone LLM으로는 LLama-7b-chat 모델을 활용합니다. 오픈 소스 모델로써, 실험 혹은 현업 분야에서 두루두루 활용하고 있는 모델이기에 오마카세를 보시는 누구나 공개된 논문 코드를 활용해 실제 적용시 별다른 제한이 없다는 점이 메리트가 있다 라고 할 수 있습니다. 또한, 논문 저자가 주장한 plug and play 실험 결과를 보면, RoG방법론이 LLaMA2 모델 뿐만아니라, 타 LLM 모델인 ChatGPT , Alpaca-7B , Flan-T5 에도 활용성이 높음을 실험 결과로써 입증했기에 범용성 또한 높다 라고 할 수 있습니다.
• Appendix 재밌는 인사이트들이 담겨 있습니다. 모두 좋은 인사이트지만, 유독 저에게 인상깊은 세 가지를 말해보자면, 1. 과연 Knowledge Base가 도메인 가릴것 없이 통용되는지를 확인하는 부분 , 2. 현업에서 사용하기 위해 필요한 Retrieval time 를 실험한 부분 , 3. Hop에 따라 reasoning 그리고 optimization 이 어떤 성능 차이가 있는지를 실험한 부분. , 4. 실제 Relation 이 어떻게 retrieval 되고, 이를 어떻게 prompt에 넣는지 예시를 가져온 부분입니다.
• 우선 첫번째 Knowledge graph transferability 입니다.

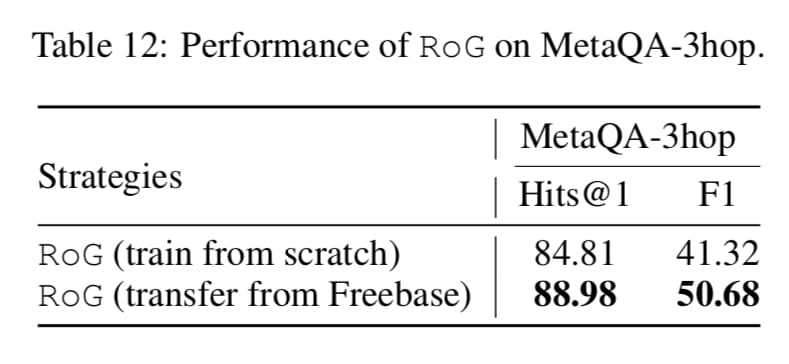
• Table 12 의 Strategies 를 비교한 내용입니다. From scratch 로 학습할지, transfer from Freebase를 할지에 따라 성능이 어떻게 바뀌는지를 실험한 표입니다.
• 직접 1000개의 샘플을 학습한것과 다르게 Freebase(Knowledge Base)를 활용한 결과가 좋다는 결과를 보이는데요. 이를 통해 저자는 본 아이디어가 Transferability, 타 도메인에도 적용이 가능할 여지가 큼을 간접적으로 제시합니다.

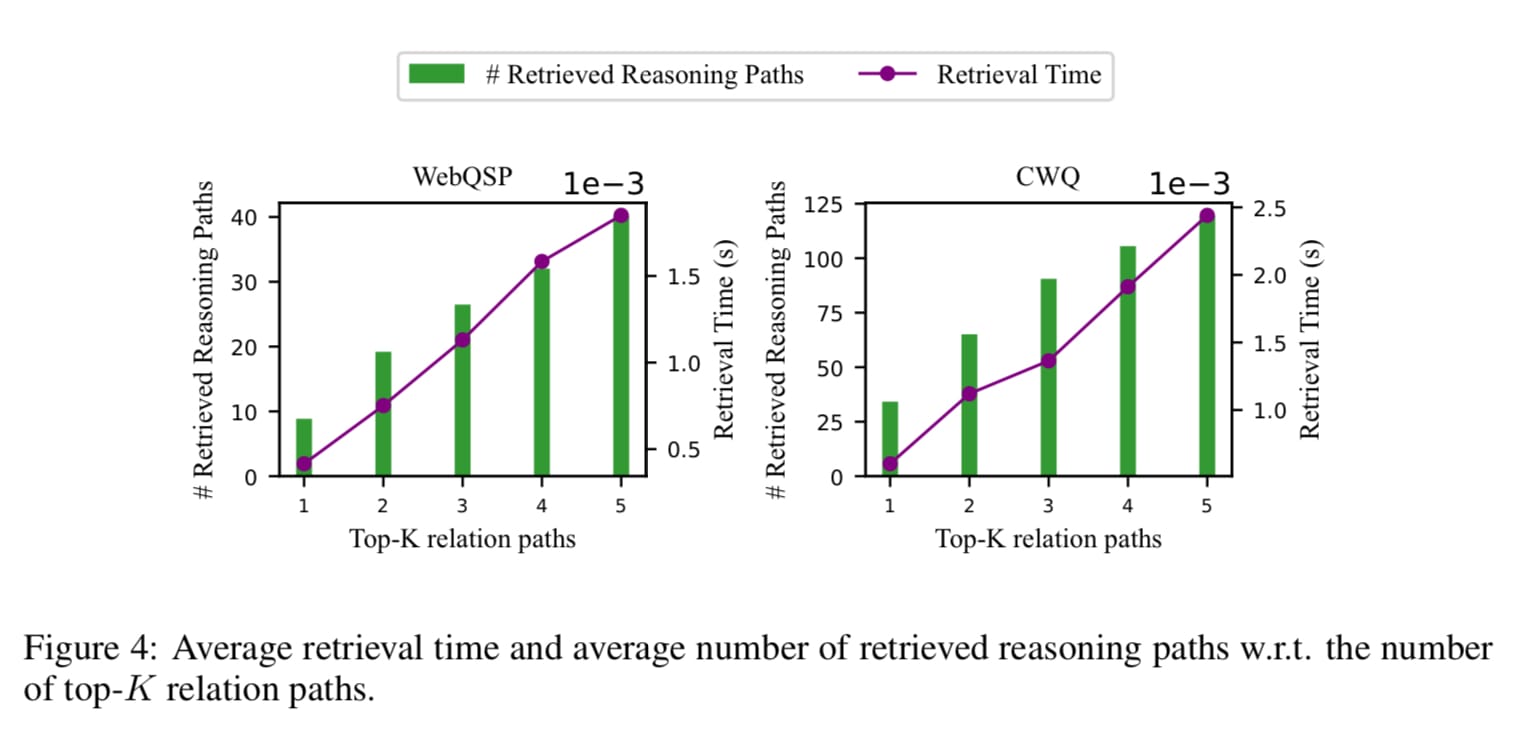
• 다음은, Retrieval time with Knowledge graph hops 입니다. 이렇게 좋은 아이디어를 현업에서 사용하기 위해 만족해야하는 조건들이 있습니다. 바로 Retrieval Time입니다. Reasoning 을 통해 LLM의 답변 성능이 좋아진다한들 고객에게 전달되기까지 시간이 기존 대비 많이 소요된다면, 오히려 고객 입장에선 불만이 생길수도 있기때문이죠.
• Figure 4를 통해 relation paths 를 1~5개 retrieval 그리고 reasoning 할 때 얼마만큼 시간이 소요되는가를 보여줍니다.

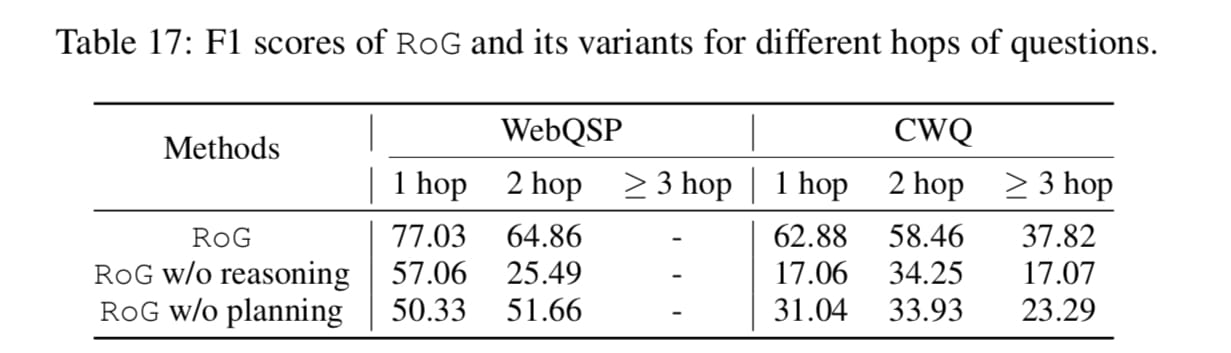
• 다음은, w/o reasoning , w/o planning 를 통해 과연 reasoning 이 필요한가 혹은 retrieval optimization 이 필요한가 를 실험한 Table 17 입니다. hop 이 늘어난다 해서 성능 또한 비례하며 증가하지 않는 부분이 재밌었습니다. 오히려 subgraph 로 들어온 정보가 노이즈로 작용함을 간접적으로 보여주는것이죠. WebQSP , CWQ 데이터셋이 서로 상반되는 결과를 보여주기에 각 데이터셋 도메인이 결과에 지장을 주지 않았을까 하는 생각입니다.

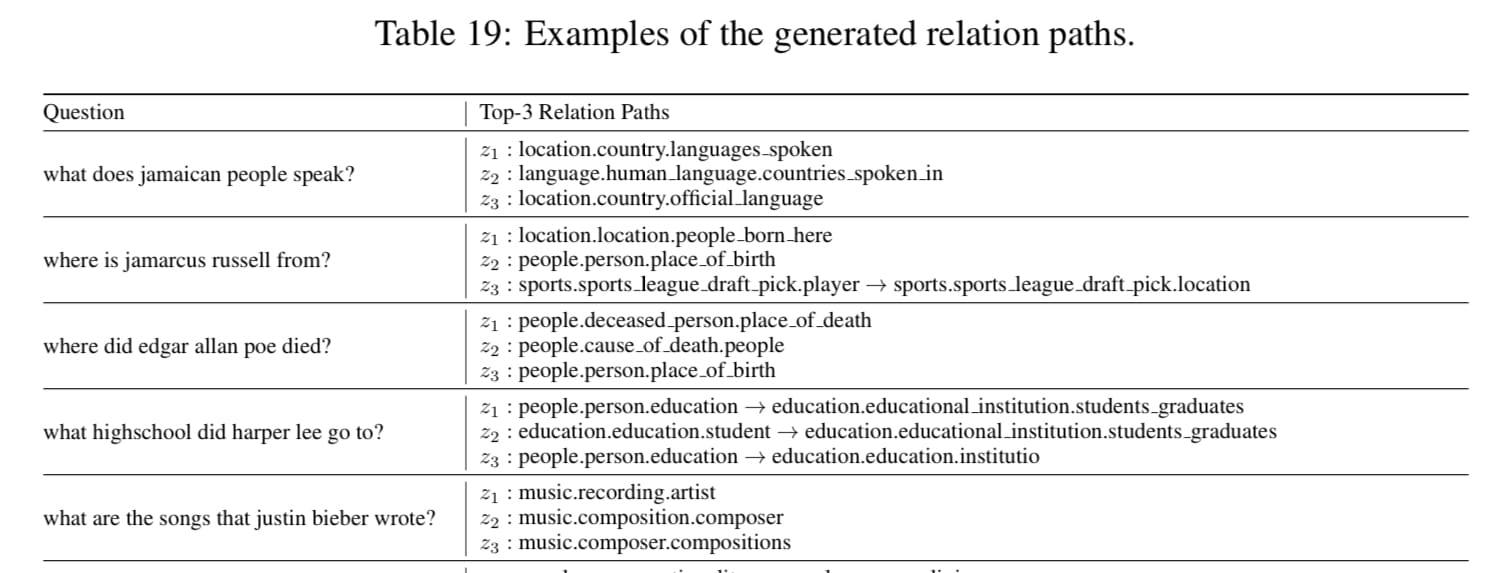
• 마지막으로는, 어떻게 retrieval 되고 retrieval 된 정보를 prompt에 넣을지 나타낸 부분인 Table 19 , 20 입니다. 실제 질문이 들어올시, 이와 관련된 path들이 어떻게 나오는지 그리고 그 path들을 어떻게 prompt template 에 들어가는지를 예시를 들어 보여줍니다.
• 추상적인 부분이라 생각했던 부분을 꼭 집어 보여줬다 생각했기에, 어떻게 Retrieval 된 결과물이 Reasoning template 에 주입될지 막연하셨던 분들에게 도움이 될거라 생각합니다.