1월 2주차 그래프 오마카세

DisoFLAG: accurate prediction of protein intrinsic disorder and its functions using graph-based interaction protein language model

keyword

• #단백질언어모델
• #신약개발
• 데이터 임베딩과 모델 구조

💡 생물학자: 악의적이고 문제를 일으키는 단백질에 대해 어떤 형태의 약물을 먼저 개발해야 하는지 예측하는 신뢰할 수 있는 방법이라고 합니다. 이 결과를 어떻게 쉽고 빠르게 확인 할 수 있을까요?

💡 생명정보학자: 단백질 잔기는 여러 가지 무질서한 기능을 가질 수 있으며, 이는 경쟁을 의미합니다. 경쟁이 있는 경우 어떻게 DisoFLAG을 개선할 수 있을까요? 상호 작용의 우선순위를 어떻게 정할 수 있을까요?

💡 AI 과학자: 데이터베이스는 얼마나 복잡할까요? 표본 외 문제는 고려해야 할 중요한 사항일 수 있습니다.

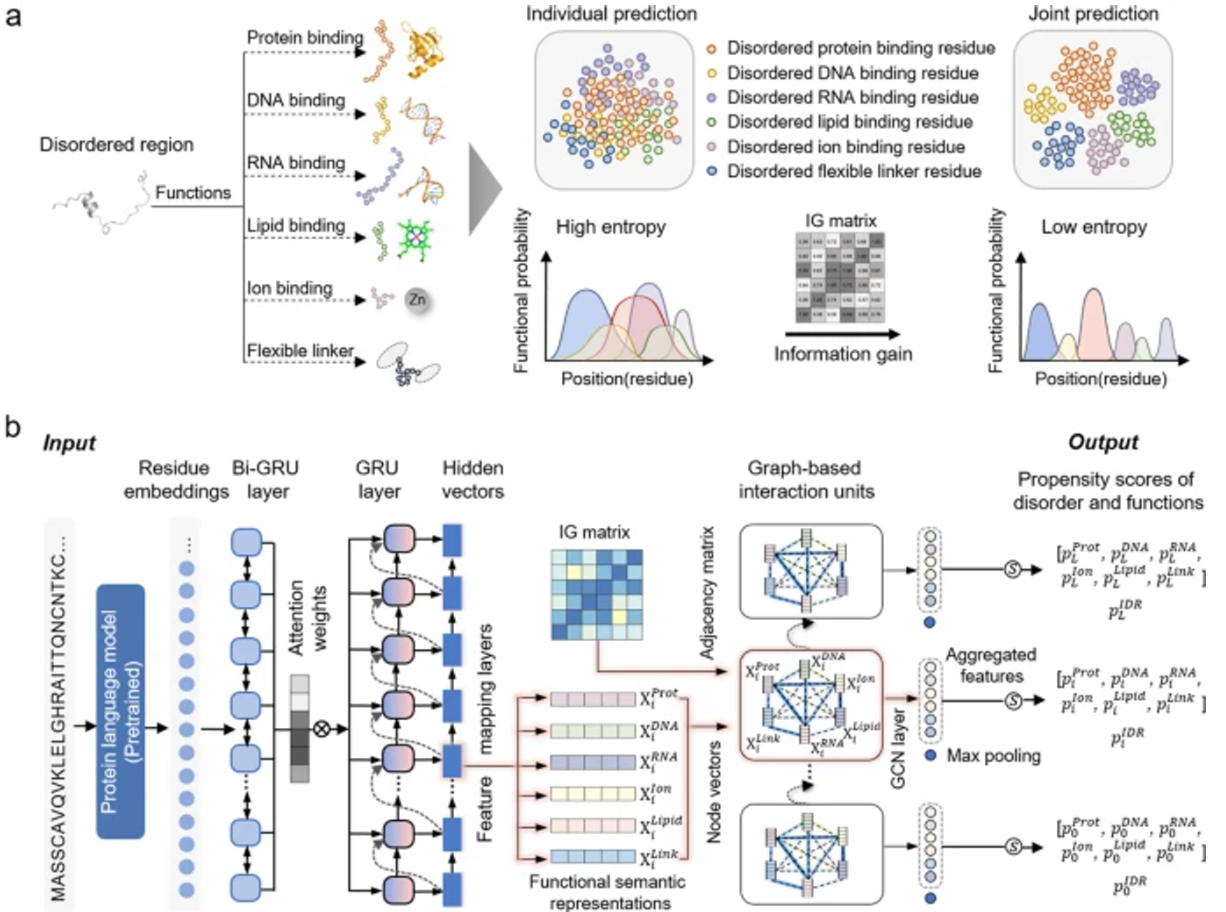
그래프 기반 상호작용 단백질 언어 모델(PLM)을 사용하여 무질서한 단백질의 기능을 예측하는 도구인 DisoFLAG를 소개하는 논문입니다.

단백질은 본질적으로 무질서한 영역에서 다양한 기능을 수행할 수 있다는 사실을 기반으로 한 모델이며, ProT5 사전 학습 모델을 참고하여 개발되었습니다.

Attention 모듈과 GRU 임베딩을 노드 특징으로, 단백질 기능 예측의 정보 엔트로피를 에지 특징으로 사용하여 단백질 내 및 단백질 간 상호작용 정보를 포착합니다.

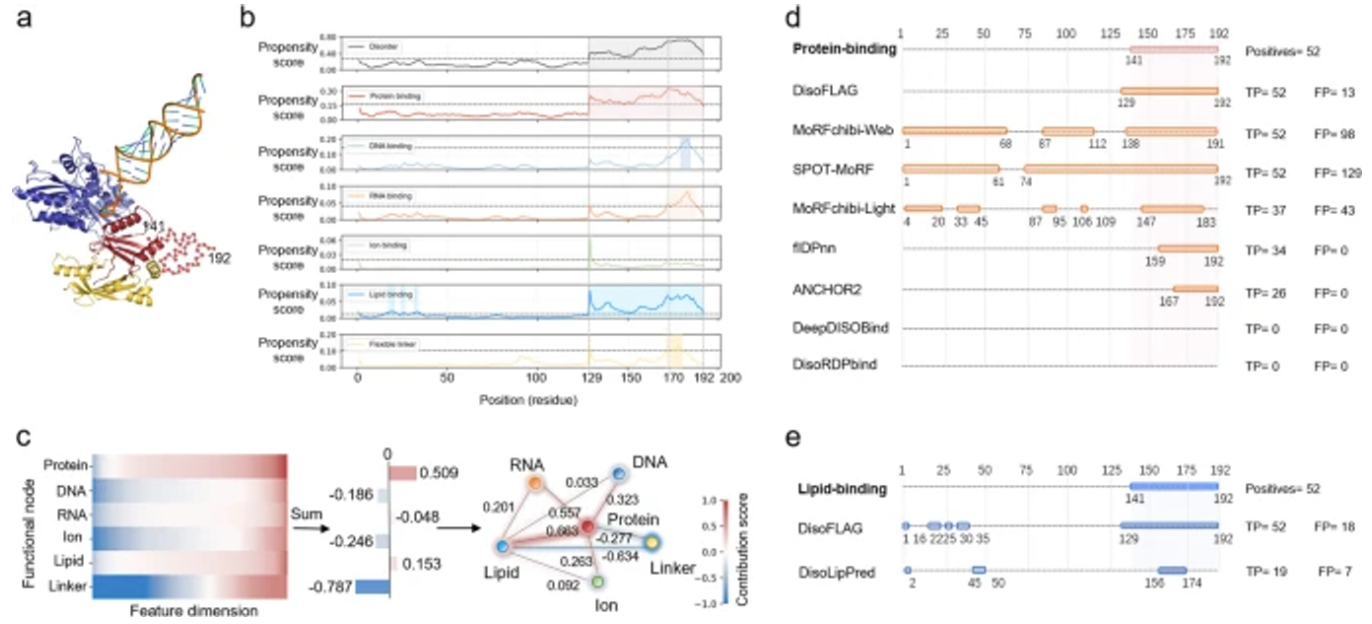
이 모델은 각 기능(장애, 펩타이드 결합, DNA 결합, RNA 결합, 이온 결합, 지질 결합, 플렉시블 링커)에 대한 성향 점수를 계산합니다. DisoFLAG는 CAID2 벤치마크와 비교하여 Dispredict3, fIDPnn, SPOT-Disorder2, AlphaFold-rsa와 같은 유사한 모델보다 우수한 결과를 보여줍니다.

이 도구는 단백질 기능에 대한 예/아니오를 잔기별로 안정적으로 알려주는 의미가 있습니다.

Contact Info

Gmail : kjwk1221@gmail.com

LinkedIn : https://www.linkedin.com/in/jiwonkimbrian/

Semi-supervised Credit Card Fraud Detection via Attribute-Driven Graph Representation

keyword

Fraud detection system, risk embedding ,heterogeneous feature, attention,time-series embedding

• 매초, 매분, 매시각 발생하는 거래 내역들을 모두 정상/이상 거래로 판별할 수 있을까요? 금융결제원 보도자료 기준으로 2021년 한 해 동안 대략 210억 건 가까이의 금융 공동망 거래가 발생했다고 합니다. 이 중 대다수는 정상 거래일 것이고, 소수가 이상 거래로 가정하고 있다면, 210억 건의 데이터 중에서 이를 판별하고 라벨링하는 것만으로도 굉장히 어려운 과제입니다.
• 대량의 데이터 중 불분명한 특성들의 데이터도 존재할 것이며, 이를 어떻게 라벨링해야할지에 대해서도 고민이 될 것입니다. 이 때, 그래프 딥러닝 모델의 장점 중 하나는 '연결'을 기반으로 추론하는 관점을 적용한다면, 이 어려운 문제를 해결하는데 일조할 수 있습니다. 이는 주로 준지도학습 특성을 갖추고 있다는 것이 핵심입니다. 본 논문의 저자도 이와 유사한 관점으로 논문을 시작하며, 논문의 독창성과 당위성을 전개해 나갑니다.
• 불분명한 특성들로 라벨링된 거래 데이터들도 많이 존재할 것이며, 이를 활용하기 위해서는 준지도학습 기반 딥러닝 모델 중 그래프 딥러닝이 이상 거래 탐지에서 유리하고 효율적이라는 것입니다.
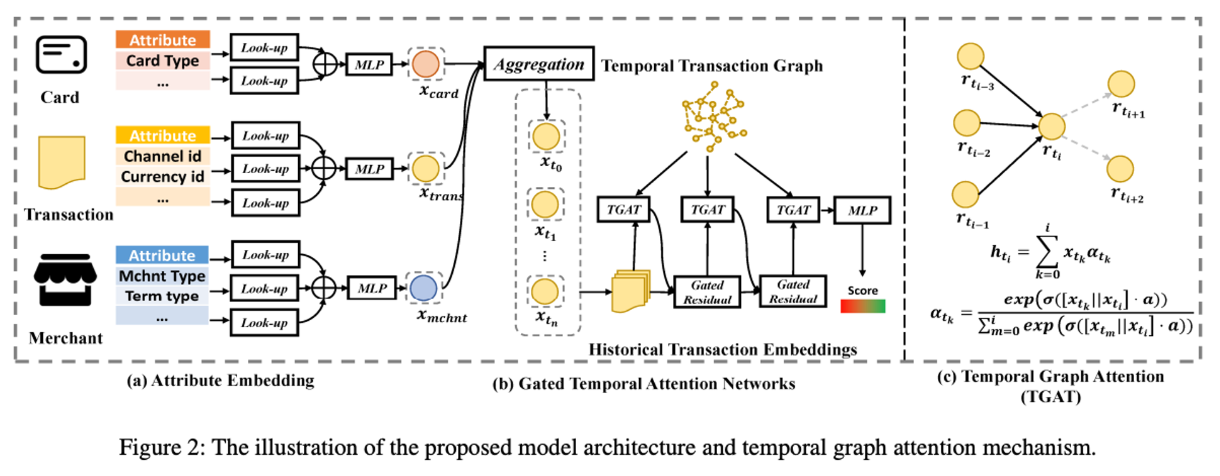
• 저자는 1. 이종 데이터 결합, 2. 시계열 그래프, 3. 위험도 임베딩 세 가지를 구현하여 그래프 딥러닝에 적용해줍니다. 먼저, 이종 데이터 결합은 각각의 이종 데이터(카드, 거래, 상점)의 특성들을 lookup-table(torch.nn.embedding)으로 매핑해줍니다. 이후, MLP(다중 레이어 퍼셉트론) 레이어를 활용해 각 특성들을 종합해 카드, 거래, 상점의 고유 난수를 만든 뒤, 그 난수들을 aggregation 해줌으로써 "언제, 무슨 카드를 활용해 무슨 상점에서"라는 맥락을 지닌 시계열 노드로 만들어줍니다.
• 다음으로 시계열 그래프를 위해서, 만들어진 시계열 노드마다 맥락을 반영해주기 위해 attention과 그 맥락의 중요도를 반영하기 위해 Gated residual 관점을 적용해줍니다. 이를 반영하게 된다면 결국, 유저가 특정 시점에 거래한 노드가 타 거래와 비교하여 거래가 상대적으로 중요한지, 중요하지 않다면 gated residual에서 활성화 함수에서 필터링이 됩니다.
• 마지막으로는 위험도 임베딩은 딥러닝 모델링 관점보다 피처 공학 관점이라 할 수 있습니다. 위험한 노드 자체의 고유 거래 정보를 가져오는 것이 아닌, 위험한 노드들과 '상관' 있는 주변 이웃들의 정보만을 가져옴으로써 '상관' 있는 이웃의 정보를 메세지 패싱해주는 방식을 활용합니다. 이때, 당연하게도 label leakage가 발생할 수 있는데, 이를 방지하기 위해 마스킹 기법을 활용해 만약 ego(central) node가 이상 거래인 노드인지 여부에 따라 임베딩 값을 change/unchange 하게끔 만들어줘서 label leakage를 방지해줍니다.
• 세 가지 요소 모두 중요하지만, 그 중 단연 돋보이는 건 마지막 위험도 임베딩이라 할 수 있습니다. 그래프 딥러닝에서만 활용 가능한 방식이라 할 수 있는데, '연결'에 기반하여 정보를 전달하여 업데이트를 할지 안할지를 조정할 수 있다는 측면에서 그래프 딥러닝의 장점을 정말 잘 살린 아이디어라 할 수 있습니다. 참고로, 저자는 label propagation 방식에서 영감을 얻어 본 임베딩 방식을 진행했다고 합니다.
• 타 방법론 대비 제안 방법론이 당연하게도 성능이 좋습니다. 추가로 여러분들께서 유념하셔야 할 점이 있는데요. 바로 F1 score와 제안 방법론 간의 연관성입니다. 참고로 저는 이상 거래 탐지에서 가장 화두가 되는 문제 중 하나가 불균형 데이터 분포이기에 이를 반영한 지표인 F1을 최우선적으로 보고 왜 이런 결과가 나왔을까?라는 고민을 굉장히 심도 있게 하고 저만의 가설을 설정해봅니다. 그 부분을 본 논문에서도 마찬가지로 Ablation Study를 통해 이야기합니다.
• Ablation study에서는 시계열 관점/위험도 임베딩 관점 여부에 따라 성능이 어떻게 바뀌는지에 대한 실험과 해석된 부분이 있습니다. 이 중 'FFSD'의 결과를 보면 시계열 관점, 위험도 임베딩 관점, 모두 반영한 관점에 따라 F1 score 성능 차이가 미미함을 확인할 수 있습니다. 결국 이를 해석해보면, imbalanced dataset의 문제를 완화하기 위해 label propagation으로부터 영감을 받아 진행한 risk embedding이 성능 개선에 유의미한 영향을 주지는 못했다.라고도 해석할 수 있는데요. 본 논문에서는 여기에 대해 추가적인 언급을 하지 않아 아쉬운 점이 있지만, 이를 그래프 오마카세 구독자 여러분께서 추론하고, 그 문제에 대해 깊게 들어가 고민한 결과를 새롭게 제안해보시면 어떨까 싶네요 :)

Contact Info

Gmail : jeongiitae6@gmail.com

Linkedin : https://www.linkedin.com/in/ii-tae-jeong/

Improving Graph Representation for Point Cloud Segmentation via Attentive Filtering (CVPR 2023)

keyword :

#Point Cloud Segmentation, #Graph convolution, #Graph Attention Filter(GAF), #Spatial Feature Projection(SPF)

summary / content

• 배경 및 문제 제기 :
  • 비유클리드 공간 상의 불규칙한 자연적 속성을 갖는 3D 포인트 클라우드 분석을 위해 최근 많은 연구들에서 그래프 컨볼루션을 활용하고 있으며, 좋은 결과를 보여주고 있습니다.
  • 하지만, 그래프 컨볼루션 모델들은 등방성 커널(isotropic kernel)을 기반으로 연산되기 때문에 입력 데이터의 공간(Spatial) 정보들을 무시하는 경향이 있습니다. 다음 문제는 차후 연구(DGCNN)에서 동적 그래프 커널(dynamic graph kernel)을 설계 & 적용함으로써 다음 문제를 완화시킵니다.
  • 또한 Transformer 모델에 영감을 받아 2020년 시퀀스 형태의 입력 데이터로 이미지를 처리, 학습하는 ViT의 성공을 기반으로, 셀프 어텐션 기법을 활용한 포인트 클라우드 분할 성능을 크게 향상시킨 연구들이 활발히 등장하고 있습니다.
  • 하지만, 셀프 어텐션 메커니즘은 저차원 상의 포인트 특징 (색상, 형태 등) 집계에 불필요한 연산을 요구하며, 특히 학습에 중요한 색상 및 기하학 정보를 일부 무시하는 경향이 있음을 본 논문에서 언급합니다.
• 다음 문제들을 동시에 해결하기 위해, 저자들은 공간 그래프 컨볼루션 및 셀프 어텐션의 장점을 모두 활용하는 하이브리드 모델 AF-GCN을 제안합니다. Fig 2는 제안하는 모델의 전체 구조를 나타냅니다.

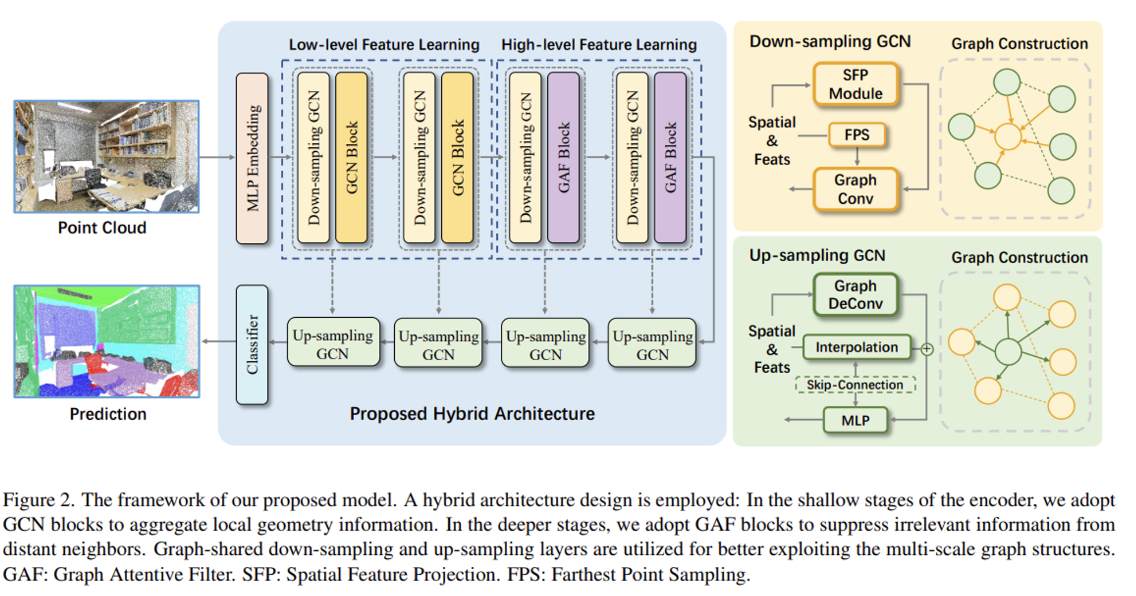
• 모델 구조
  • 저자들이 제안한 AF-GCN의 하이브리드 구조은 크게 인코더 및 디코더 2가지 구조로 나누어볼 수 있습니다. 여기에서 인코더는 다운 샘플링 연산 및 그래프 컨볼루션으로 구성된 저차원 특징 학습(Low-level feature learning) 단계와, 본 논문에서 새롭게 제안하는 그래프 어텐션 필터링(Graph Attention Filtering) 모듈을 적용한 고차원 특징 학습(High-level feature learning) 단계로 구성되어 있습니다.
  • 인코더 단 (상단 구조):
    • 저자들은 다운 샘플링 기법으로 FPS (Farthest Point Sampling)을 채택하였습니다. 위 방법은 이전 PointNet++(2017) 논문에서 제안되었으며, 그 이름처럼 가장 멀리 떨어진 포인트를 중심 포인트로 샘플링하는 방법입니다. 다음은 랜덤 포인트 샘플링 방법보다 그 샘플링되어 나온 포인트들의 무작위성이 크게 감소하기 때문에 더 나은 수렴성(better convergence)을 갖는다고 알려져 있습니다.
    • 다음 샘플링된 포인트들이 주어지면, 그래프 컨볼루션 블록(GCN Block)에 다음 포인트를 통과시켜 저차원 특징정보들을 학습합니다. 다음 GCN Block은 본 논문에서 제안하는 공간 특징 사영(Spatial Feature Projection, SPF) 모듈이 추가된 그래프 컨볼루션 연산이 수행됩니다. 다음 과정은 식 8로 공식화하였습니다.

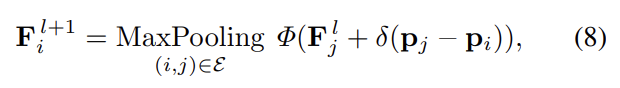
• 이후, 고차원 특징정보 학습을 위해 셀프 어텐션 메커니즘의 강점을 가져온 GAF(Graph Attentive Filtering) 블록을 설계하였습니다.

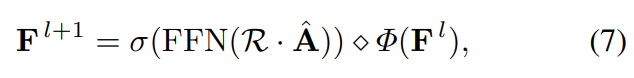
• Fig 3은 위의 설명들을 뒷받침하는 GCN 블록 및 GAF 블록의 내부 구조를 나타내고 있습니다.

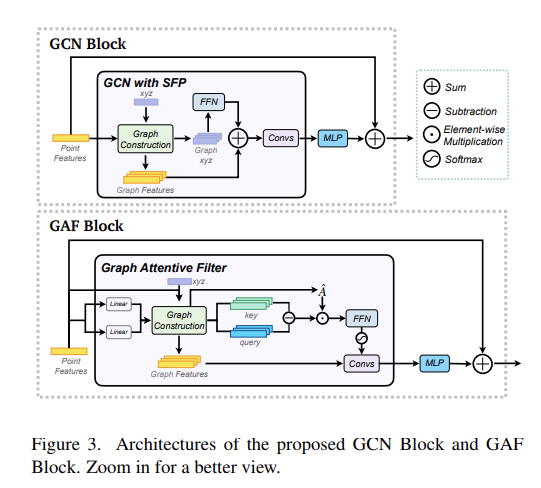
• 디코더 단 (하단 구조)

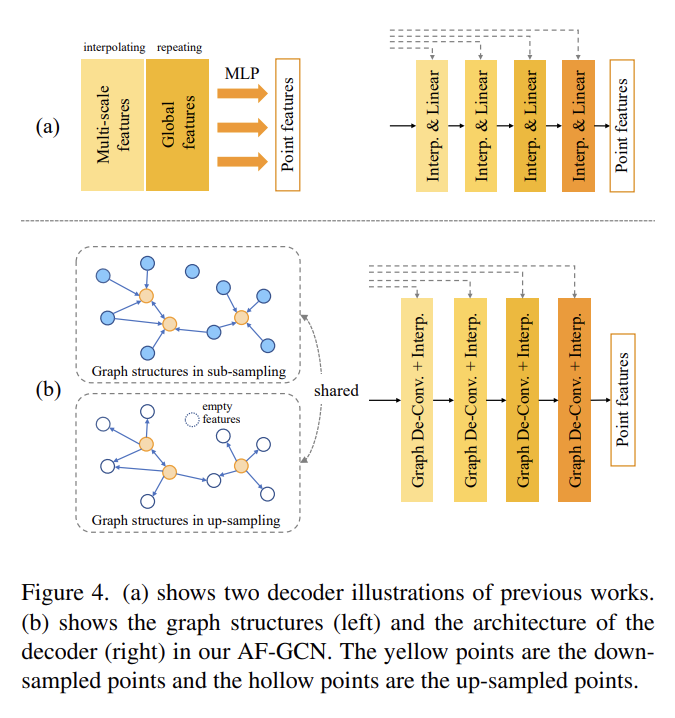
• 본 저자들은 샘플링 이전, 이후의 그래프 구조를 그대로 유지하면서(Graph-shared), 식 9로 정의한 그래프 역컨볼루션(Graph De-convolution ) 및 그 과정에서 생성되는 empty feature 포인트를 보충하기 위한 Trilinear Interpolation 순서로 디코더를 구성하였습니다. 본 설명은 식 10으로 공식화할 수 있습니다.

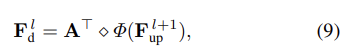
• 요약하자면, 저자들은 본 논문에서 새로운 모듈 (GAF, SPF)을 설계하여 그래프 컨볼루션에 적용한 하이브리형 그래프 네트워크 구조 AF-GCN 제안하였습니다.
• AF-GCN은 동일한 그래프 구조 상에서 다운 샘플링 및 업 샘플링 과정을 통해 원 그래프 토폴로지 정보를 그대로 유지하면서 포인트의 low & high-level한 특징을 모두 포착할 수 있는 장점을 가져오면서, 포인트 클라우드 분할 문제에서 좋은 성능을 얻어낼 수 있습니다.
• 개인적으로 다음 논문을 읽으면서 들었던 생각을 공유드리면, 문제 제기에서 언급된 그래프 컨볼루션 및 셀프 어텐션의 강점들을 챙기면서 그 단점들은 새로운 모듈들을 통해 효율적으로 처리하는 아이디어가 흥미로웠습니다.
• 하지만 Fig 3의 인코더 단에서 반복적으로 다운 샘플링 포인트 기반으로 풀링된 그래프를 반복적으로 구성(’Graph construction’) 하는 과정이 약간 비효율적이라고 느껴졌습니다.
• 또한 직관적으로 GAF 모듈이 어떻게 불필요한 포인트 정보를 필터링 하는지에 대해 이해가 잘 되지 않았습니다. 식 7에서 상관관계 행렬 R과 포인트 거리차이 기반으로 업데이트 된 인접행렬 A_hat을 dot product함으로써 필터링되는 것으로 이해할 수 있을 것 같습니다만, 정확하게 와 닿지는 않았던 부분이었습니다.

Contact Info

Gmail : jhbae7052@gmail.com

LinkedIn : https://www.linkedin.com/in/jihun-bae-757302289/

Twitter : @jhbae1184