24년 6월 3주차 그래프 오마카세
Multi-class Brain Tumor Segmentation using Graph Attention Network
Keywords
Graph Attention Network, Brain tumor segmentation, Supervoxel clustering
Summary
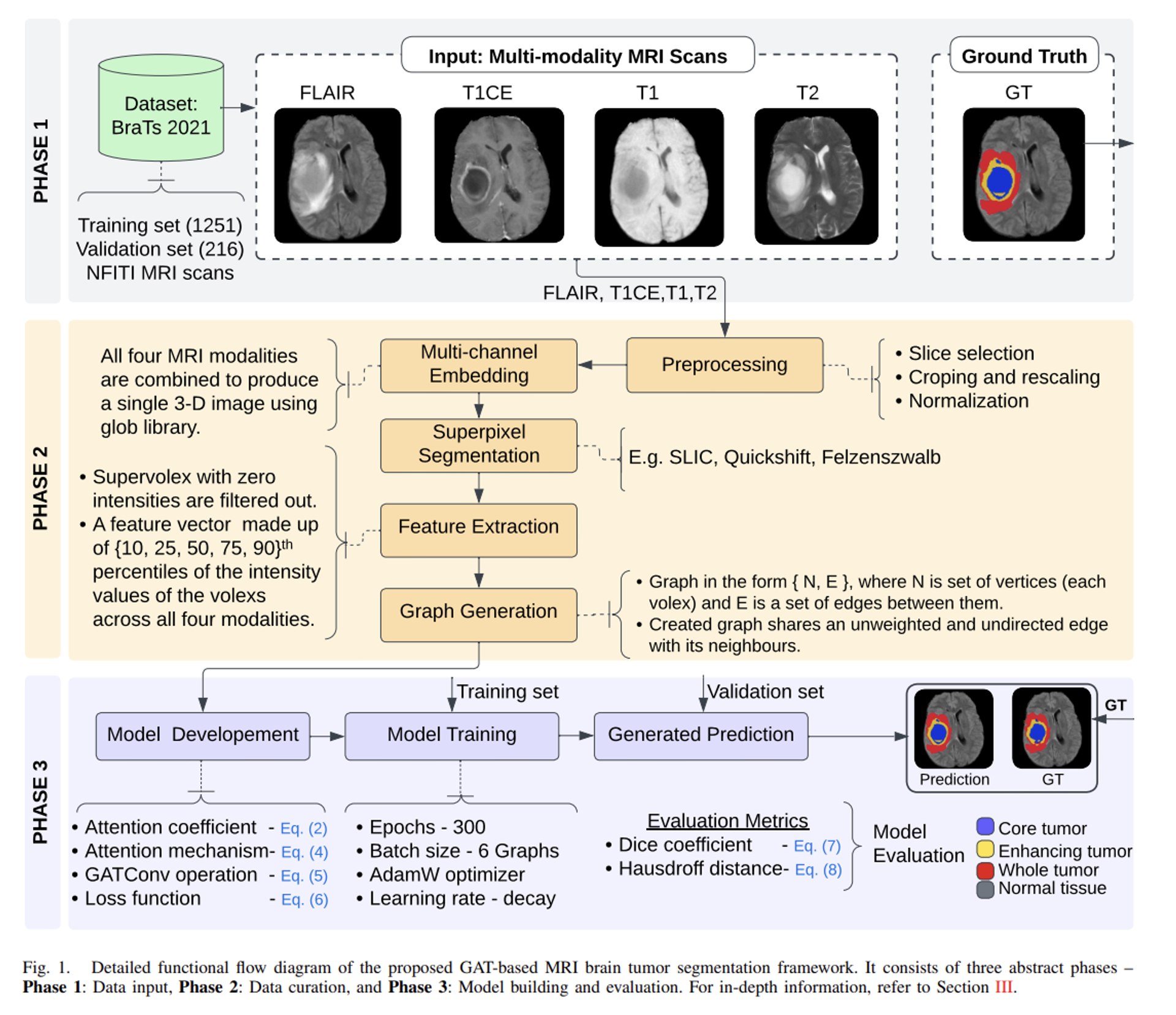
- 뇌 종양 분할 문제에서의 그래프 활용도 역시 많은 연구자들로부터 관심을 받고 있습니다. 종양 클래스 별 고유한 불규칙 형태, Curvature 등과 같은 기하학적 특징 정보들을 그래프로 인코딩하여 학습시켰을 때 인상적인 결과를 얻어낼 수 있음도 수많은 연구를 통해 밝혀진 사실입니다.
- 소개해드릴 논문에서는 static magnetic field 내 비균질성 및 gradient magnetic field 내 비선형성 등의 어려운 문제로 남아있는 뇌 종양 분할 문제에서 어떻게 해당 뇌 종양 클래스 영역을 그래프로 잘 표현시키며, 효율적인 그래프 학습을 위한 어텐션 네트워크를 활용한 사례를 보여줍니다.
- 저번에 소개해드린 Superpixel 그래프에서의 저차원 공간으로 강제 맵핑시켜 얻어낸 결과는 MRI의 내재적인 볼륨 정보를 모두 잃어버리는 한계점이 존재합니다. 다음을 잘 보존시키기 위해, 해당 논문에서는 Supervoxel이라는 3D 픽셀 클러스터링 기법을 활용합니다.
- 먼저 MRI modalities 별 뇌 종양 추출 및 인지 장점을 그대로 활용하기 위해 전처리 과정에서 이들을 하나의 3D 이미지로 변환시킨 후, 다양한 픽셀 클러스터링 기법을 활용하여 Supervoxel로 표현합니다. 그리고 그 위에 빠른 그래프 표현 알고리즘으로 활용되어지는 Region Adjacency Graph (RAG)을 기반으로 그래프를 구성합니다. 다음 그래프는 유의미한 종양 픽셀들의 특징들을 각 노드에 그대로 유지하면서 훨씬 적은 개수의 노드로 축소시킬 수 있는 효과를 얻어낼 수 있습니다.
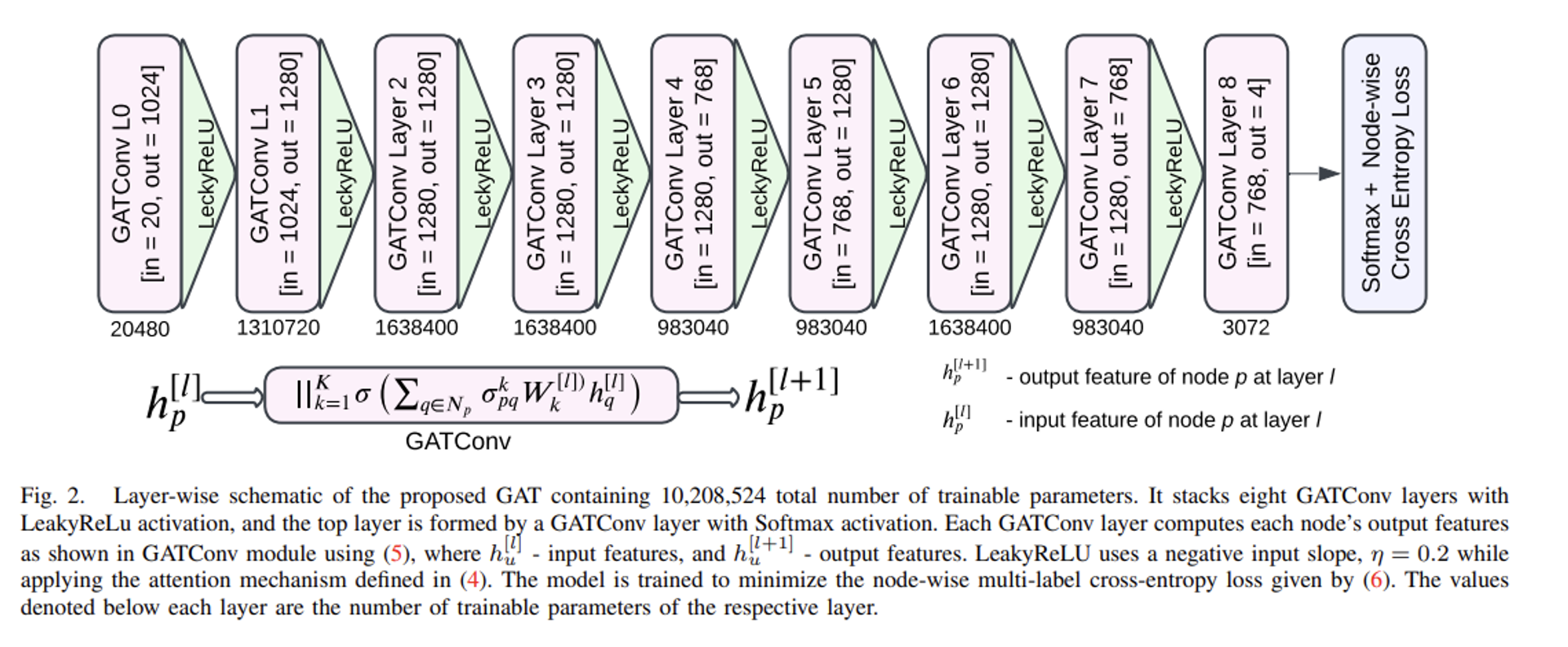
- 구성된 Supervoxel 그래프를 효율적으로 학습하기 위해, 저자들은 GAT를 다음과 같이 구성하여 학습에 활용합니다. 기존의 GAT 메커니즘을 그대로 활용하여, 동일한 레이블을 갖는 이웃 노드들 사이에 더 높은 가중치의 엣지를 주입하고, 셀프 어텐션의 학습 과정의 안정화를 위해, 다음 연구에서는 멀티헤드 어텐션 기법을 적용하였습니다.
- 저자들은 실험적으로 그래프 어텐션 메커니즘의 효과를 통해 다중 클래스 뇌종양을 보다 정확하게 분할할 수 있음을 나타냅니다. 또한 Supervoxel 그래프를 입력으로 사용함으로써 학습 속도를 향상시키고, 추론 시간을 약 1.7초 줄일 수 있었습니다.
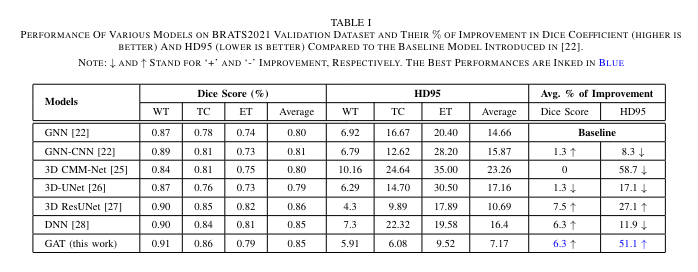
- 간략히 요약하자면, 이번에 소개해드린 논문은 픽셀 클러스터링을 활용하여 구성한 그래프를 활용하는 사례를 보여주었으나, 기존 논문과는 달리 MRI의 내재적인 볼륨 정보 등의 손실을 방지하기 위한 Supervoxel 그래프를 활용하고, 뇌 종양 분할 문제에서 그래프 어텐션 메커니즘의 효과를 확인해볼 수 있었습니다.
