GraphOmakase

1월 4주차 그래프 오마카세

H2-FDetector: A GNN-based Fraud Detector with Homophilic and Heterophilic Connections

[Paper Info]

[keyword]

imbalancedData, FraudDetection ,Heterophily

[Content]

지금 이 순간에도, 사기꾼들은 선량한 시민들을 대상으로 악의적으로 재화를 편취하기 위한 사기 수법을 개발하고 시행하고 있을 것으로 생각됩니다. 특히, 온라인 채널의 발달로 여러 플랫폼을 통한 상호교류가 증가하면서, 오프라인 대비하여 온라인 사기 건수가 급증하고 있다고 합니다.

이러한 증가의 이유를 고려해보면, 사기꾼들이 범죄 대상의 특성을 고려하여 '초개인화 사기'를 적용하고 있기 때문입니다. 예를 들어, 연령대가 높은 노년층을 대상으로는 '자녀들'이라는 키워드를 활용한 사칭 범죄가 증가하고 있으며, 반면에 연령대가 낮은 청년층은 '사회경험이 적다'는 점을 악용하여 향후 취업 등에 제한이 있을 것이라는 두려움을 조장하여 공적 권력을 사칭한 범죄가 늘어나고 있습니다.

이러한 초개인화 사기에 대응하기 위해서는 새로운 방법이 필요합니다. 다양한 방지책이 있겠지만, 본 논문에서는 수법 패턴 간 유사성을 더욱 정교하게 고려하기 위해 '유사한' 패턴과 '유사하지 않은' 패턴의 특성을 동시에 고려하는 임베딩 방식을 제안합니다.

과거의 방식들은 주로 '유사한' 패턴만을 고려하여 임베딩했지만, 이로 인해 유사하지 않은 패턴들이 누락되는 문제가 발생했습니다. 범죄에 활용되는 수법과 그렇지 않은 수법을 정확히 구분해야 한다는 중요성을 간과한 셈인데, 이는 범죄에 활용되지 않는 패턴도 범죄 활용 패턴을 구분짓기 위한 중요한 특성 중 하나일 것입니다.

논문에서 언급한 'homophily(동질성)'와 'heterophily(이질성)'는 현재까지 '유사'라는 표현으로 설명해왔습니다. 간단히 설명하자면, homophily는 나와 연결된 노드가 나와 유사한 특성을 가지고 있는지를 측정하는 지표이며, 반대로 heterophily는 유사하지 않은 특성인지를 측정하는 지표입니다.

앞서 언급한 대로, 네트워크 내의 연결된 노드들 간의 'homophily'와 'heterophily'를 정확하게 측정하고 이를 임베딩에 반영하는 것이 중요합니다.

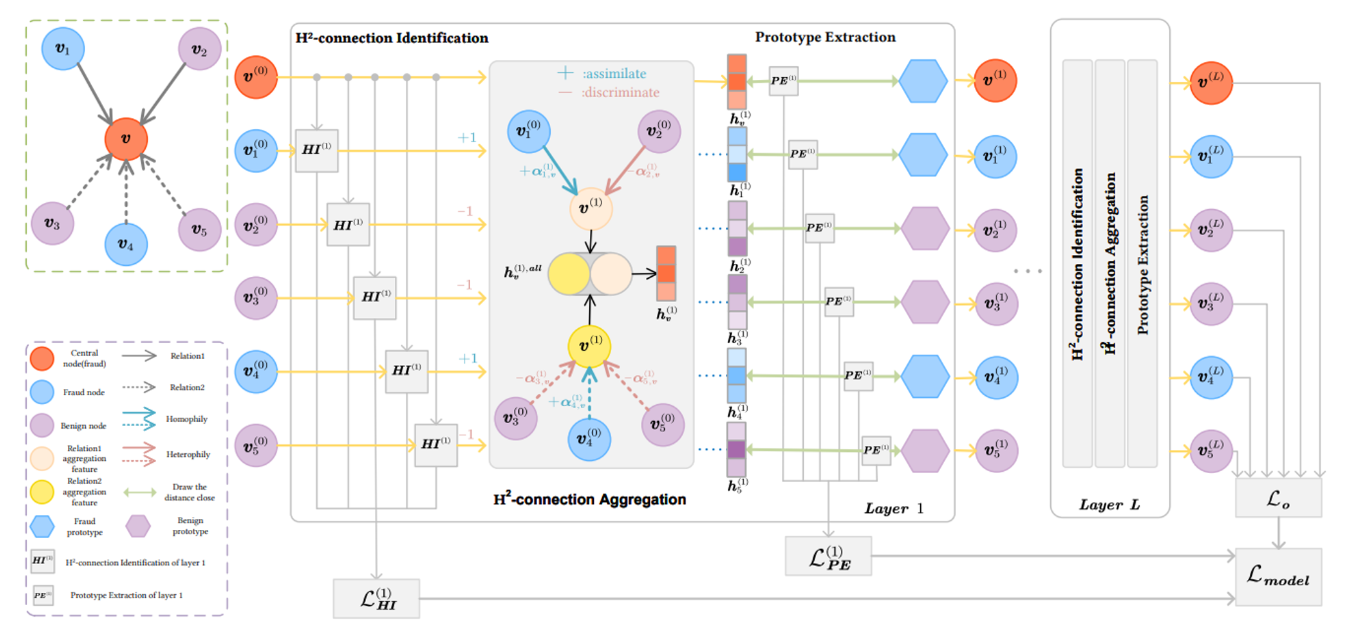
Label Identification (라벨 식별):
- Edge label 정보를 활용하여 각 엣지의 고유 특성을 학습하고 정량화합니다.
- 각 엣지에 대한 가중치 부여를 위해 embedding layer에 입력하고, 이후 MLP 레이어를 통과시켜 각 엣지의 특성을 구분합니다.
- 사용되는 라벨은 edge type이며, 각 엣지의 타입을 정교화하기 위해 학습 Loss를 조정한 보조 손실(auxiliary loss)을 활용합니다.
Connection Aggregation (연결 집계):
- 정량화된 엣지의 고유 특성을 기반으로 homophily와 heterophily를 집계합니다.
- 기존의 attention 방식은 단순 가중합으로 이루어져 homophily 특성과 heterophily 특성을 구분하기 어렵다는 문제를 해결하기 위해, 중심 노드를 기준으로 각기 다른 연결들을 불러온 서브그래프에 attention을 적용하고 이를 연결(concat)합니다.
- 이를 통해 중심 노드를 기준으로 한 각기 다른 엣지 특성이 반영된 임베딩 값을 얻습니다.
Prototype Extraction (프로토타입 추출):
- Inter와 Intra의 다른 클래스들의 특성을 반영하기 위해, 거리 기반으로 대표적인 정상과 비정상 노드를 프로토타입화합니다.
- 각 노드에 대해 대표 노드들과의 거리 차이를 측정하여 '정상'과 '비정상'에 대한 기준을 추가로 고려합니다.

제안된 방법론은 undersampling을 진행한 CARE-GNN 및 PC-GNN 아키텍처와 비교하여 우수한 성능을 나타냅니다. 금융 분야에서는 각 거래가 어떤 종류의 거래였는지 라벨링이 어렵기 때문에, 다른 산업 데이터에 비해 데이터 간 분포 불균형이 더 심합니다. 이에 논문에서 제안하는 모델은 imbalanced 데이터에 대한 고려가 필요한 모델들보다 뛰어난 성능을 보여주어, heterophilic의 중요성을 강조하는 부분으로 해석됩니다.
추가적으로, 불균형에 대한 측정 결과를 보면 Figure3와 모델 성능 결과가 분포 측면에서 상관관계가 있습니다. 특히, 데이터의 불균형 비율이 높은 경우 undersampling 대신 heterophily를 고려한 방식이 성능적으로 더 우수함을 확인할 수 있습니다.
이에 따라 heterophilic을 반영하는 방법이 매우 중요하다고 판단됩니다. 4.4 Ablation study에서는 heterophily를 attention으로 고려한 방식과 prototype으로 inter 및 intra class를 거리 측면에서 고려한 방식을 각각 제외한 모델 간의 성능 비교를 수행했습니다. 결과적으로 prototype 방식이 더 뛰어나게 나타났는데, 이는 주어진 anchor 노드로부터의 거리가 heterophily 특성을 더 잘 구분하고 반영한다고 해석됩니다.
edge connection type을 이용하여 homophily와 heterophily를 측정하는 방법은 매우 독창적이며 설득력 있는 논문으로 판단됩니다. 특히, transformer가 지배적인 구조로 인정받는 시대에 attention을 어떻게 활용할지에 대한 다양한 아이디어들이 트렌드가 되고 있는 가운데, 이 논문은 그 트렌드를 효과적으로 반영한 것으로 보입니다.

[Contact info]

Email - jeongiitae6@gmail.com,

Linkedin - https://www.linkedin.com/in/ii-tae-jeong/

Paper : Two sides of the Same Coin : Heterophily and Oversmoothing in Graph Convolutional Neural Networks (ICDM 2022)

[Paper info]

link : https://arxiv.org/abs/2102.06462

Code : https://github.com/Yujun-Yan/Heterophily_and_oversmoothing

[Keyword]

: Heterophilic Graph, Oversmoothing problem, Node Profiling with Signed Edges

최근 노드 분류 도메인의 그래프 표현 학습 방법들에서, 많은 관심을 받으면서 활발하게 연구되어지고 있는 주제가 바로 Heterophily graph 이지 않나 싶습니다.
Heterophily graph란, 동일한 클래스 혹은 유사한 특징을 갖는 노드들이 연결되어 있는 Homophily graph의 반대 개념으로써, 즉 동일하지 않거나 비유사한 특징을 갖는 노드들이 연결되어 있는 그래프 구조를 의미합니다. Online Transaction network, Molecular networks 등과 같은 실제 세계에서의 그래프 (Real world graph) 데이터 대다수가 Heterophily한 성질을 가지고 있습니다.

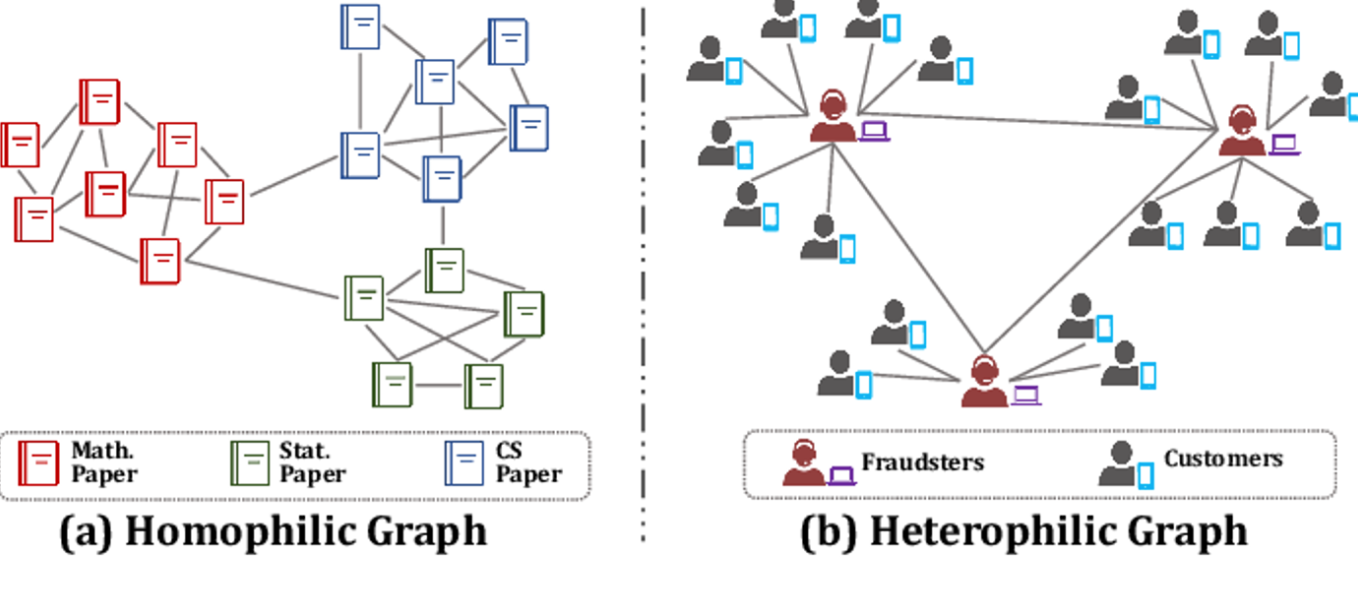
이미지 출처 : 'graph neural networks for graphs with heterophily : A survey(2022)

Heterophily한 그래프 데이터들은 일반적으로 homophilic 그래프 구조 데이터 상에서 잘 동작하는 기본 GCNs 모델의 학습 성능에 제한을 주기 때문에, 결과적으로 상당한 성능 하락을 초래하게 됩니다.
이전 오마카세 게시글에서 제가 소개해드렸던 FAGCN 역시 다음 문제를 해결하기 위해 제안되었으며, 다른 노드들로부터 전달되는 메세지의 저주파수 및 고주파수 요소들에 각각 가중치를 부여함으로써, 적응형으로 전달되는 메세지의 중요도를 조절하는 방법을 학습하도록 함으로써 Heterophilic graph 구조에서의 GCNs 성능 하락을 완화합니다.
이번에 소개해드릴 논문은 제목 그대로 GCNs에서 Heterophiliy 성질과 Oversmoothing 문제를 연결하여 두 문제를 동시에 분석하고, 엣지 가중치의 부호를 학습하도록 하여 GCNs의 레이어를 통과할 때마다 Feature space 상에서 학습된 노드의 움직임 (Movement)을 모델링 (Profiling)합니다.
결론적으로, 본 논문의 저자들은 이론적인 증명을 통해 부호화된 엣지 가중치를 추가하는 것이 Heterophilic한 그래프에서의 성능을 향상시킬 수 있으며, Oversmoothing 문제 역시 완화할 수 있음을 주장합니다.

Fig 1은 이웃 노드의 메세지 집계 과정에서 Homophily 성질과 Degree의 차이에 따라 유동적으로 변화하는 노드 표현의 결과를 보여주고 있습니다. FIg 1를 통해, 기존 GCNs 모델의 Homophily 그래프 상에서만 잘 동작한다는 한계점을 보여주고 있습니다.
- 왼쪽 표는 Homophily한 노드의 Degree 및 강도에 따라 MR (잘못 예측한 비율)의 결과값을 행렬형태로 표현하였으며, 오로지 높은 Homophily의 높은 Degree를 갖는 노드 (Case 3)만이 MR을 낮출 수 있었으며, 그외의 Heterophily한 경우 (Case 1 & 2)는 MR이 더 높아진 결과를 보여줍니다.
- Fig 1의 오른쪽 그림에서는, 위의 모든 Case들에 대한 그래프 구조에서의 중심 노드 i가 이웃 노드들로부터 메세지를 전달 받기 전,후의 예측한 클래스의 확률분포의 변화를 보여주고 있습니다.
- Bar Plot을 통해, Heterophily 그래프에서의 중심 노드 i는 메세지 집계 이후 다른 클래스로 예측해버리거나 (Case 1) 혹은 확실치 못한 올바른 예측 (Case 2)을 보여주고 있으며, 오로지 Case 3의 Homophily 그래프 구조에서만이 메세지 집계 이후에 더욱 확신적인 올바른 예측을 보여주고 있습니다.
이러한 결과를 바탕으로, 저자들은 (Case 1 & 2의) Heterophily 그래프 구조 상에서 MR이 높아지는 이유를 표준 메세지 전달 메커니즘을 통해 전달되는 다른 클래스 정보의 혼합으로, 표현 업데이트의 결과가 less distinguishable되어버리는 Oversmoothing 문제에 집중합니다. 다음은 Homophily 혹은 Heterophily한 구조에 상관없이, 모든 엣지에 동일한 양의 가중치를 부여하는 기존 GCNs의 한계에 있음을 언급합니다.
Theorem 3.3의 이론적 증명을 통해, 저자들은 그래프 구조정보(연결성, Structure-based) 및 특징 기반 (Feature-based) 상관관계를 바탕으로, 각각 다른 부호화 엣지 가중치를 할당하도록 학습하였을 때 두가지 문제 모두를 해결할 수 있음을 보여줍니다. 다음을 학습하는 모델은 GGCN의 명칭으로 제안되었습니다.
실험 결과에서도 heterophily 성질 (Table 1) 및 oversmoothing 문제 (Table 2)를 해결한 GGCN의 효율성을 보여주고 있습니다.

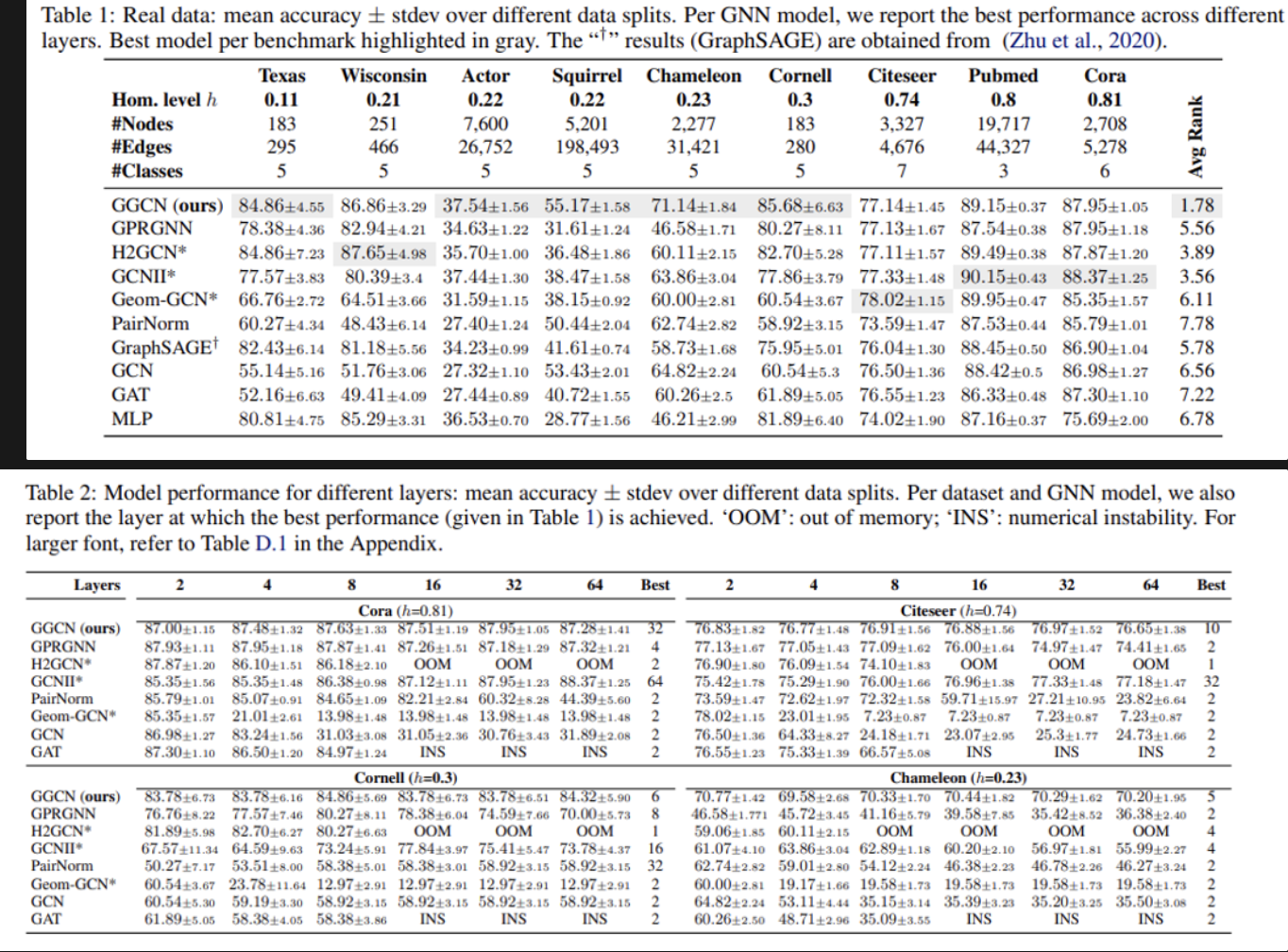
결론적으로, 다음 논문에서는 Heterophily한 그래프 구조에서 한계점을 보이는 기존의 GCNs을 Oversmoothing 문제와 연결짓고, 그래프 구조정보 (Homophily or Heterophily) 및 메세지 집계 과정으로 전달되는 메세지 특성 (Similar or Dissimilar Message)간의 상관관계를 바탕으로 음의 부호 엣지를 적절하게 할당할 수 있도록 학습 메커니즘을 개선함으로써, 제안하는 GGCN의 효율성을 이론적으로, 실험적으로 입증하였습니다.
전통적인 그래프 도메인 뿐만 아니라, 그 외의 컴퓨터 비전 쪽에서의 그래프 표현 학습이 많이 연구되고 있습니다. 해당 분야에서, 해당 작성자의 연구 주제인 Point Cloud Analysis에서, Point Cloud 데이터를 적절하게 표현한 그래프 상에 자주 등장하는 구조가 바로 Heterophily 입니다.
Supplementary에서 해결하고자 하는 문제들을 이론적으로도 자세히 증명하고 있으므로, 수학적으로 이해하기가 쉽진 않았던 부분이 많았으나 연구 결과의 신빙성을 높게 가져갔던 논문입니다.

[contact info]

Gmail : jhbae7052@gmail.com

LinkedIn : https://www.linkedin.com/in/jihun-bae-757302289/

Twitter : @jhbae1184