24년 5월 4주차 그래프 오마카세

Graph Structure from Point clouds : Geometric Attention is All You Need.

NIPS 2022

배지훈

paper link

official code

The question of how to produce a graph structure in these problems is usually treated as a matter of heuristics, employing fully connected graphs or K-nearest neighbors. In this work, we elevate this question to utmost importance as the Topology Problem. We propose an attention mechanism that allows a graph to be constructed in a learned space that handles geometrically the flow of relevance, providing one solution to the Topology Problem.

Introduce

• 수많은 ML tasks 에서 포인트 클라우드 데이터의 그래프 표현 학습 활용이 빈번하게 연구되고 있습니다. 다음 핵심은 얼마나 표현된 그래프가 해당 포인트 클라우드의 기하학적 특징을 잘 모델링하는가 에 대한 해답을 제시하는 것입니다.
• 다음 논문은 입자 물리학의 jet tagging 이라는 다소 생소한 분야에서, 각 에너지 입자의 포인트들을 그래프로 표현하여 임베딩한 관계성 학습을 통해 "jet" 입자의 클래스를 분류하는 작업에 활용한 예시를 보여줍니다.
• 휴리스틱한 Fully connected graph 혹은 KNN graph의 계산 집약적 및 비효율성 문제를 해결하고자 보다 더 효율적인 그래프 표현 방법에 대한 아이디어 연구가 활발하게 진행되고 있습니다. 해당 논문에서는 이전 연구모델 GravNet 아키텍처 내에 Geometry-constrained attention mechanism을 도입하여 효율적인 그래프 표현을 위한 방법을 제안하고 있습니다.

Methodology

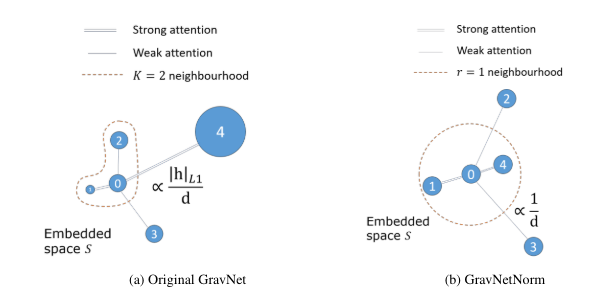
• 제안하는 GravNetNorm은 그래프의 각 노드에 대한 최적의 이웃 크기를 동적으로 학습하여 결정하는 Attention mechanism을 통합하여 기존 GravNet 아키텍처를 조정합니다.
• 직관적으로 고정된 이웃 크기를 갖는 정적 KNN 알고리즘과 크게 대조되며, 동적 알고리즘 기반 학습 프로세스를 통해 각 포인트에 대한 최적의 이웃 수를 지속적으로 학습함으로써 다양한 데이터 세트 및 작업에 대한 모델의 적응성을 개선하고, 해당 모델의 분류 예측 정확도를 크게 향상시킵니다.
• Fig 1를 보면, 기존 GravNet은 각 노드가 가지고 있는 특징 벡터 h의 크기를 사이 거리 d로 나누어 정의한 이웃 범위를 기반으로, 상대적으로 가깝고 영향력이 큰 이웃 노드들을 취하는 방식이었습니다. 하지만 노드 간 근접성 차이로 인해 더 많은 영향력을 행사하는 노드들의 영향력을 완전히 반영하지 못할 수 있습니다.
• 다음 문제를 해결하기 위해, 본 논문의 저자들은 Geometry-constraint attention operator을 제안합니다. 다음 operator는 임베디드 공간의 오로지 Geometric Proximity 정보만으로 정의된 이웃 노드들만 고려하도록 Attention mechanism을 제한함으로써 위의 문제를 완화하고, Fully connected graph의 계산 리소스를 선형적으로 크게 줄일 수 있었다고 합니다.
• Jet tagging 문제와 같이 적절한 그래프 토폴로지를 선택하는 것이 중요한 Task에서, Fully connected graph의 대부분의 노드 쌍 연결이 predicted results과 직접적인 연관성이 없음을 발견하였습니다. 다음 사실로부터 저자들은 어떤 노드가 가장 관련성이 높은지 학습하는 Attention mechanism을 설계하였으며, 이러한 연결의 가중치를 높여 모델의 예측 능력을 향상시킬 수 있음을 설명합니다.
• 특히 Sparsely connected graph의 경우, 특정 메시지 전달 단계에서 어떤 노드가 가장 많은 정보를 제공하거나 다른 노드와 관련이 있는지가 확실하지 않습니다. 대다수의 GNNs (e.g. ParticleNet) 에서는 주어진 그래프가 Homophilic한 토폴로지 구조를 갖는 강한 제약 조건을 가정하기 때문에, 위의 사실을 온전하게 고려하지 못할 수 있음을 지적합니다.
• 비유사한 노드와 연결되는 그래프 (i.e. Heterophily)를 고려해야만 하는 경우가 존재하기 때문에, 이러한 그래프 토폴로지 구조를 모두 고려할 수 있도록 GravNetNorm은 Second, independent latent space에서 다음 Attention mechanism을 적극적으로 활용하여 만족스러운 결과를 얻어낼 수 있었음을 설명합니다.

Conclusion

• 해당 논문에서 제안하는 GravNetNorm은 Geometric Attention Mechansim의 잠재력을 강조하여 관련 operator를 도입함으로써 더욱 효과적으로 의미적인 이웃 노드를 효과적으로 포함할 수 있었고, 또한 그래프 학습에서 중요한 그래프 토폴로지 (Homophily or Heterophily) 선택의 문제를 해결했습니다.
• 또한 휴리스틱하게 그래프 표현 방법으로 많이 활용되어지는 KNN의 정적 이웃 노드 정의의 비효율성 및 Fully connected graph의 계산 복잡도를 효과적으로 크게 낮출 수 있었습니다.
• Jet tagging이라는 다소 생소한 분야를 Target Task으로 잡았으나, 이에 국한되지 않고 일반적인 포인트 클라우드 상의 새로운 그래프 표현 방법을 제안하였으며 거대 스케일 데이터셋으로의 확장 가능성 등 여러가지 이점들을 보여주었던 새로운 가능성을 보인 논문이라고 생각합니다.

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn