24년 12월 2주차 그래프 오마카세
Graph Neural Networks for Edge Signals: Orientation Equivariance and Invariance
paper link: https://arxiv.org/abs/2410.16935
official code : https://github.com/dfuchsgruber/eign?utm_source=catalyzex.com
- 이번 주 오마카세는 엣지 신호 모델링 측면에서 Direction, Orientation의 2가지 독립적 엣지 특성을 모두 포착할 수 있는 Direction-aware Topological Model, EIGN을 소개한 논문을 전달해드리고자 합니다.
- 다양한 시나리오에서는 엣지의 2가지 속성들, Direction 및 Orientation, 을 모두 고려하였을 때 해당 신호를 정확하게 모델링할 수 있습니다. 전자는 노드의 메세지가 인접 노드로 전달되는 방향에 따라 유향 및 무향 엣지의 신호적 특성을 포착하지만, 후자는 그래프 전체에서 흘러가는 Flow 측면에서 해당 신호의 특성을 포착합니다. 각각을 개별 엣지가 갖는 절대적 및 상대적 방향성으로 생각해보면 좋을 것 같습니다.
- 아래의 교통 시스템 예시를 통해 쉽게 이해할 수 있을 것 같습니다. 해당 시스템에는 Direction ('One way', 일방 통행) 및 Orientation (차량 이동 방향, 좌측 혹은 우측)이 모두 존재하고 있으며, 이러한 정보들을 정확하게 모델링하여 교통사고 등의 위험을 방지할 수 있을 것입니다.
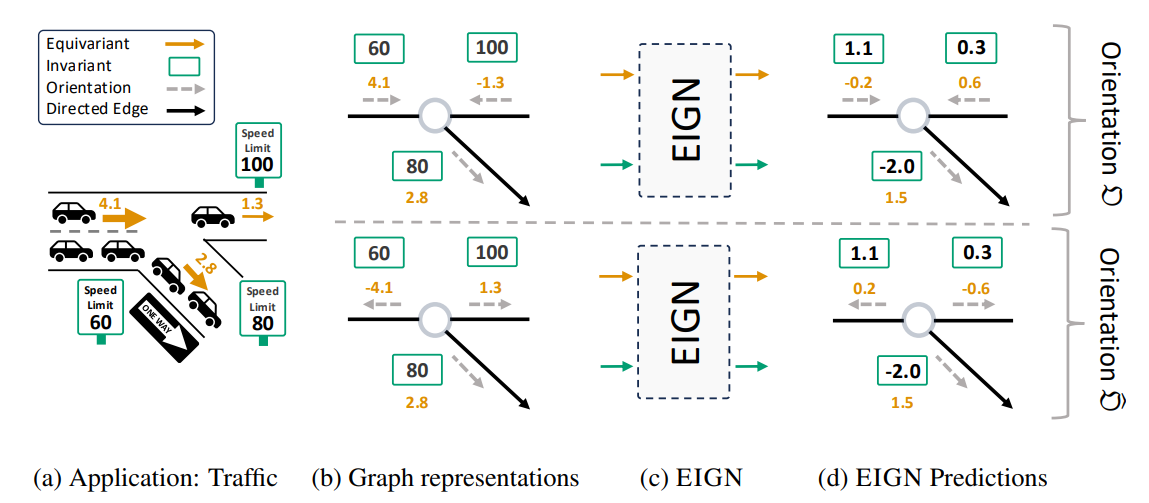
- 기존 토폴로지 모델 (TSP)은 Orientation-Equivariant한 성질, 즉 reference orientation (e.g. 기준 방향: 좌측 이동)에 따른 상대적 방향성 정보 (e.g. 같은 방향: 양의 부호, 반대 방향: 음의 부호), 을 정확하게 포착할 수 있도록 설계되었으나 Direction 정보에 따른 변동 (e.g. 일방 통행이냐, 양방 통행이냐)에 따른 일관된 결과를 얻어낼 수 없습니다. 교통 시스템의 경우, 아래와 같이 일관되지 못한 결과로부터 사고와 같은 위험을 초래할 수 있습니다.
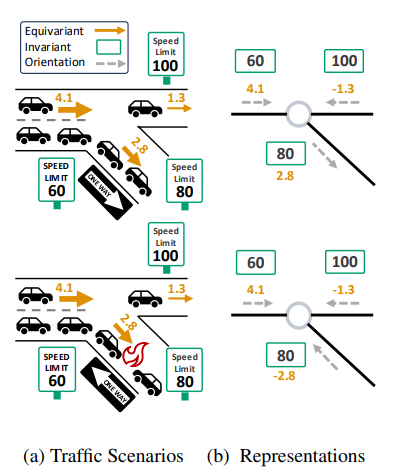
- 추가적으로 제한 속도와 같은 Orientation-Invariant한 정보까지 활용할 수 있다면 해당 모델의 효율성이 높아질 것으로 예상됩니다.
- 즉, EIGN은 Direction-aware한 엣지 신호들 중 orientation-equivariant 및 invariant한 엣지 신호들에 대한 일관된 예측 결과를 만들어내는 모델로 설계되었습니다.
Desirable Properties for Edge-level GNNs
- Direction에 따른 일관된 결과를 얻어내기 위해, 한 가지 제약조건을 겁니다. Direction-consistent Orientation, 즉 엣지 Direction과 Orientation의 방향이 동일한 경우를 고려하는 것을 의미하며 다음의 정확한 의미를 이해하는 것이 해당 논문에서 매우 중요합니다.
- 다음 제약조건은 Orientation의 방향을 Direction의 방향과 동일시 하게 가정함으로써, 반대로 생각하면 해당 Orientation의 방향성에 따라 무향 엣지에서도 Direction을 (상대적으로) 파생할 수 있다고 볼 수 있겠습니다. 다시 말하면, Direction 및 Orientation을 고려해야할 때의 정확한 엣지 신호 모델링을 할 수 있다라는 사실 (여기에서 desiderata로 표현)을 단순 Orientation의 정보만으로도 Direction 정보를 파생할 수 있다는 의미로 해석할 수 있겠습니다. 본문 설명은 아래와 같이 나와있습니다.
💡
Restricting these properties to direction-consistent orientations means that both properties only need to hold regarding the arbitrary orientation of undirected edges. This allows models to break both desiderata for the orientation of directed edges, which enables using their orientation to encode direction.
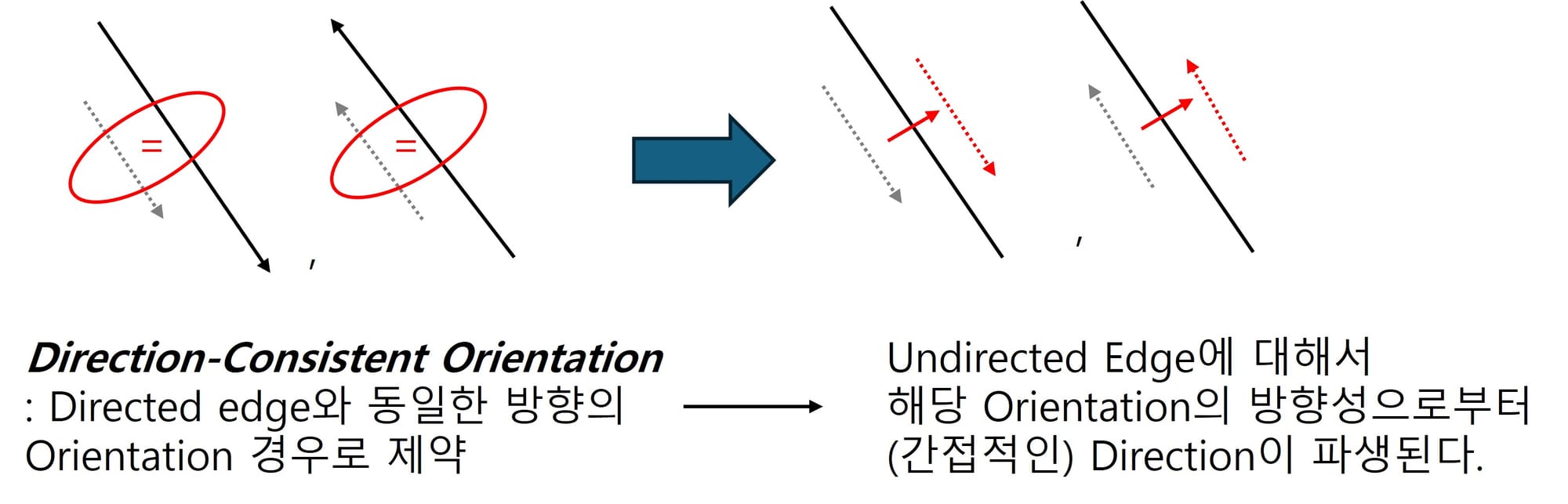
- 위의 제약조건으로부터 direction-consistent한 엣지 신호의 Orientation-Equivariant & Invariant한 성질만 고려해도 될 수 있게 기준이 완화되었습니다. (이러한 사실로부터 논문 제목에 Direction이 없는 Orientation Equivariant and invariant만 넣어둔 게 아닐까 예상해봅니다.) 다음을 해당 논문에서는 Joint Orientation Equivariant & Invariant로 정의하였습니다.

EIGN : An Orientation-Equivariant and Orientation-Invariant Model
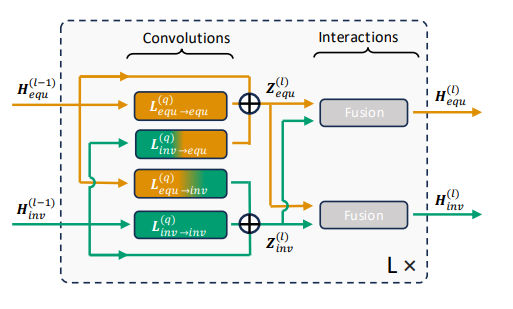
- EIGN 모델은 다른 그래프 신경망과 마찬가지로 메세지 전달 메커니즘으로 학습이 진행됩니다. 특이한 부분으로, Graph shift operator로써 Edge Laplacian (L)을 활용하여 인접 엣지들 중 동일한 성질의 신호 (equ - equ 및 inv - inv) 뿐만 아니라 다른 성질의 신호 간 관계성 (equ - inv) 까지 고려합니다.
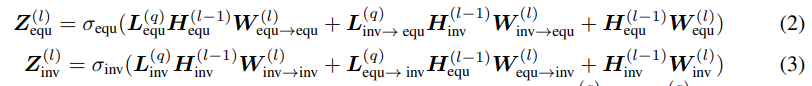
- 여기에서 Lequ은 Equivariant함을 만족하기 위해 아래와 같이 정의합니다. 여기에서 consecutive의 의미는 인접 엣지들의 Direction-consistent Orientation이 연속적인 방향 관계를 의미합니다.

- Convolutions part에서는 식 2,3과 같이 Equivariant 및 Invariant한 엣지 신호의 연산이 진행됩니다. 동일한 성질 및 다른 성질과의 관계성 정보를 모두 받아 residual connection을 통해 이전 신호에 추가합니다.
- 본인 엣지의 Equivariant 및 Invariant한 성질을 위의 관계성에 추가하기 위해 Fusion operation은 아래 식 4,5와 같이 Edge Laplacian을 제외한 연산으로 진행됩니다.
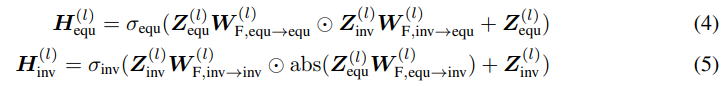
- 여기에서 Point-wise production 및 absolute는 위의 joint orientation equ/inv 성질을 만족하는 연산으로 사용되었습니다. 다음 사실은 Appendix A에서 자세하게 설명합니다.
- 이러한 연산 과정을 통해 모든 엣지의 신호 모달리티 간 상호작용 모델링이 가능하다는 점을 본 논문에서 언급합니다. 하지만 다음은 인접한 엣지 신호 정보를 컨볼루션 및 그 상호작용을 모델링한 것일 뿐, 방향성에 대한 정보를 고려한 것은 아닙니다. 그로부터 무향 엣지로부터 파생된 Direction의 정보인지, 본래 유향 엣지의 Direction 정보인지를 구별할 수 없습니다.
- 다음을 명확하게 구별하기 위해 Complex phase shifts을 통해 엣지 방향성을 표현하는 Magnetic Node Laplacian 성질을 기반으로 유향 엣지의 Direction의 정보를 포착할 수 있는 Edge Laplacian을 새롭게 제안합니다.
💡
The Magnetic Node Laplacian represents edge direction through complex phase shifts of magnitude πq for some fixed hyperparamter q.
Orientation-Equivariant And Orientation-Invarinat Laplacians
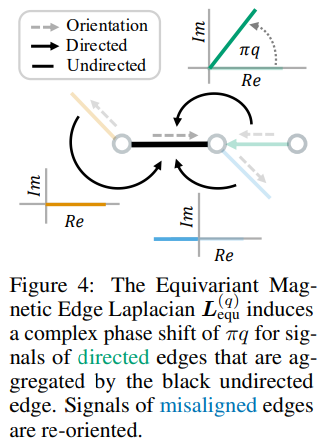
- Lequ의 정의로부터 황색 및 파란색 무향 엣지의 파생된 Direction으로부터 Equivariant 성질을 포착할 수 있습니다. 하지만 초록색 유향 엣지의 Direction의 Equvariant 성질을 구별하여 포착하기 위해, Lequ(q)=(Bequ(q))H Bequ(q)는 Complex phase shift 기반의 boundary operator로부터 동일하게 정의됩니다.
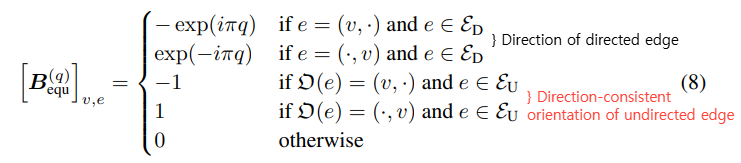
- 여기서 Complex phase shift의 부호는 엣지의 Direction에 따라 결정됩니다. 즉, 첫번째 조건식(v, )은 노드로부터 나오는 outflow, 두번째 조건식( , v)은 노드로 들어가는 inflow한 엣지 신호에 해당합니다.
- 유향 엣지는 사실상 Direction 정보가 존재하기 때문에 파생된 Direction이 필요하지 않습니다. 그로부터 기존과 동일하게 해당 Complex phase에 부호를 부여하여 방향성을 조정합니다.
- D, U는 lower & upper adjacency한 포함 관계를 의미합니다.
- 정리하면, 해당 연산자는 인접 엣지 신호의 Direction이 무향 엣지의 파생된 Direction인지, 유향 엣지의 본래 Direction인지를 먼저 판별 (유향 엣지의 경우 식 8의 1,2번째 조건식으로 처리, 무향 엣지의 경우 식 8의 3, 4번째 조건 처리)한 이후 집계하는 과정으로 진행됩니다.
💡
The key difference is that L (q) equ applies a complex phase shift to the signals of directed edges before aggregating them instead of just re-orienting them by flipping their sign.
Lequ(q) is a jointly orientation-equivariant operator as per Definition 4.1 for the (arbitrary) orientation of undirected edges (even if they are adjacent to directed edges).
It, however, specifically breaks orientation equivariance for directed edges by inducing complex phase shifts: Changing the direction of a directed edge flips the sign of the complex phase shift that is applied before aggregation.
Lequ(q) is a jointly orientation-equivariant operator as per Definition 4.1 for the (arbitrary) orientation of undirected edges (even if they are adjacent to directed edges).
It, however, specifically breaks orientation equivariance for directed edges by inducing complex phase shifts: Changing the direction of a directed edge flips the sign of the complex phase shift that is applied before aggregation.
- 마찬가지로 Linv(q)=(Binv(q))H Binv(q)도 유향 엣지에 대한 Complex phase를 적용한 아래의 Boundary operator를 통해 정의합니다.
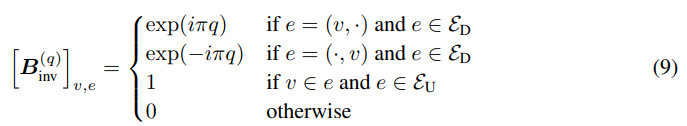
- 저자 깃허브에 오피셜 코드가 아직 올라오지 않았으나, 코드를 보시면서 아이디어를 이해해보신다면 글로만 보기에는 복잡할 수 있을 내용이 더욱 직관적으로 와닿을 수 있지 않을까도 생각해봅니다.
- 다음 논문의 핵심만을 간략하게 정리해보겠습니다.
- 다음 논문은 기존 TSP 모델의 엣지 신호 모델링 과정에서 Orientation-equivariant한 특성만을 포착하고 추가적인 Invariant한 특성 및 실제 엣지의 Direction의 정보를 포착하지 못한다는 한계점을 극복하고자 한다.
- Direction 정보를 포착하기 위한 한가지 제약조건으로 유향 엣지의 Direction 방향과 동일한 Orientation 방향을 가지고 있다고 고려한다. 다음을 무향 엣지로 가정하였을 때 해당 Orientation 방향으로부터 간접적인 Direction 정보를 파생할 수 있다.
- 그로부터 EIGN의 메세지 전달 과정에서 해당 Direction 정보가 유향 엣지의 본래 정보인지, 무향 엣지의 파생된 정보인지를 구별하기 위해서 새롭게 Complex phase shift 기반의 edge Laplacian을 제안한다. 그로부터 Orientation-equivariant 및 invariant 특성을 포착하는 Lequ(q) 및 Linv(q)을 활용하여 EIGN의 동작 메커니즘을 정의한다. (식 2~5)
- 정리해본 핵심 중 2번째의 제약조건 및 3번째의 Complex phase shift 기반 edge Laplacian을 새롭게 정의하는 아이디어를 이해하셨다면 충분히 해당 논문이 주는 인사이트를 얻어갈 수 있을 것으로 생각합니다. Appendix에서 증명과정을 자세하게 제공하고 있으니 신빙성을 위해 참고해보시는 것을 추천드립니다.
[Contact Info]
Gmail: jhbae1184@akane.waseda.jp
Twitter (X): @jhbae1184
