Signal Processing on Simplicial Complexes (2)

paper link : https://arxiv.org/abs/2106.07471

배지훈

• 이전 게시글에서 소개해드린 TSP에 대한 기본 핵심 개념들 (Simplicial complex, Face / Co-face, Boundary operator)을 독자 여러분들께 전달해드렸었습니다. 꽤나 낯설고 생소한 개념들이 많이 있을 수 있어서, 최대한 쉽게 접하실 수 있도록 열심히 정제해보았습니다만, 저의 필력이 워낙 좋지 않은 부분도 분명히 있을 것이라 처음 접하시는 독자분들께서 쉽게 숙지하시기에 충분히 어려우실 수 있으실 거라 생각합니다.
  • 확실한 것은 GSP와 마찬가지로, TSP 역시 탄탄한 수학적 이론 및 배경을 바탕으로 구축된 도메인이기 때문에 대수적 이해를 필요로 하는 부분이 존재합니다.
  • (수학에 정말 약한..) 저 역시 완벽하게 이해하지 못한 부분들이 존재할 수 있습니다. 따라서 독자 여러분들과 반복적으로 상기하면서 숙지하고자 하는 것이 중요할 것 같습니다.
• 그로부터 이전 글에서 소개해드린 핵심 개념들을 반복적으로 리뷰해보는 것이 좋을 것 같은 생각을 하게 되었습니다. 간략하게 Recaps 해본 후, 이번 오마카세에서 전달해드릴 내용은 TSP 도메인에서 정말 중요한 역할을 수행하는 Hodge Laplacian matrix 정의 및 얻어낼 수 있는 Spectral properties를 해당 논문의 설명을 따라가며 하나하나 이해해보도록 하겠습니다.

Recaps to previous post

• k-simplex란 유한 노드 집합 (V)에 대하여 k+1개의 구성 요소를 갖는 V의 하위 집합으로 정의됩니다. 즉, 노드로부터 구성되는 그래프 요소 및 복합 요소 - 노드 (vertex), 엣지 (edge), 삼각형 (triangle), 사면체 (tetrahedron) .. - 모두를 통칭하는 개념입니다. 여기에서 k는 simplex의 차수 (order)로 정의하며, 최고로 높은 k 차수를 해당 simplex의 차원 (dimension)으로 정의합니다.
  • 0-simplex : 1개의 노드로부터 구성되는 그래프 요소 = 노드 (Vertex)
  • 1-simplex : 2개의 노드로부터 구성되는 그래프 요소 = 엣지 (Edge)
  • 2-simplex : 3개의 노드로부터 구성되는 복합 요소 = 삼각형 (Triangle)
• Simplicial complex (X)는 k-simplices의 집합 개념으로, 반드시 아래의 포함 속성 (Incidence property)을 만족해야 합니다.
  • Incidence property : X에 속한 임의의 k-simplex에 대하여, 다음 k-simplex의 하위 집합 역시 X에 속해야 한다.
• 포함 속성을 기반으로, k-simplex 및 (k+1)-simplex 사이의 관계성을 표현하는 Face / Co-face 개념을 정의할 수 있었습니다.
  • Face : k-simplex가 (k+1)-simplex의 하위집합에 속한다면, 다음 k-simplex는 (k+1)-simplex의 Face가 된다.
  • Co-face : 위의 경우, (k+1)-simplex는 k-simplex의 Co-face가 된다. Co-face는 Face 관계의 simplex보다 항상 cardinality가 1개 더 많다.
• Simplices 간의 Face / Co-face 관계를 대수적으로 인코딩하기 위해, 저희는 반드시 방향성 (Orientation)을 정의했어야 했습니다. 다음 방향성으로부터 인코딩 행렬인 Boundary operator의 개념을 유도할 수 있기 때문입니다.
  • 방향성 (Orientation of simplicial complex) : 일반적으로, 각각의 simplex에 대하여 할당된 구성 노드들의 레이블 값의 오름차순으로 지정합니다. 하지만 데이터에 따라 다른 적합한 방법으로 방향성을 정의할 수 있었으며, 방향 그래프 (direct graph)와는 구별되는 개념이라는 것을 반드시 기억하셔야 합니다.
  • 다음 방향성으로부터 다른 차수 (different order)의 simplices 간 관계성을 추적할 수 있습니다. 구체적으로 Boundary operator를 통해서 이루어집니다.
• Boundary operator (B_k): 임의의 (k-1)-simplex와 k-simplex 사이의 Incidence property 및 Orientation 정보를 인코딩하는 행렬 연산자 개념입니다. 다음 행렬의 행에는 k-simplex 정보가, 열에는 (k+1)-simplex 정보가 할당됩니다.
  • k=1의 경우 (즉, 노드와 엣지 사이의 관계), 0이 아닌 양의 행렬 요소 (+1)는 해당 엣지를 통해 해당 노드로 들어오는 신호 (inflow) 정보를 인코딩하며, 0이 아닌 음의 행렬 요소 (-1)는 해당 엣지를 따라 해당 노드로부터 빠져 나가는 신호 (outflow) 정보를 인코딩합니다. 0의 요소는 포함되지 않은 경우를 나타냅니다.
  • k=2의 경우 (즉, 엣지와 삼각형 사이의 관계), 0이 아닌 양의 행렬 요소 (+1)은 해당 삼각형을 구성하는 데 해당 엣지가 포함되어 있으며, 그 방향성이 서로 일치하는 경우를 인코딩합니다. 0이 아닌 음의 행렬 요소 (-1)은 해당 삼각형에 해당 엣지가 포함되어 있으나, 그 방향성이 반대인 경우를 인코딩합니다. 0의 요소는 포함되지 않은 경우를 나타냅니다.
• B_k 행렬을 통해 저희들은 해당 simplicial complex 내부의 모든 요소들 간 관계성을 정확하게 이해할 수 있으며, TSP 관점에서 B_k 요소들의 신호적 특성을 분석할 때 유의미한 해석을 가능하게 해줍니다.
• 구체적으로, 다음은 이번주에 소개해드릴 B_k 기반의 Hodge Laplacian matrix를 통해 수행됩니다.

The Hodge Laplacian as a shift operator for simplicial complex (Chap 4.2 참고)

• 거듭해서 말씀드리는 부분이지만, TSP 도메인에서 정말 정말 중요하면서도 기본이 되는 Hodge Laplacian을 설명드리고자 합니다.
• Hodge Laplacian은 GSP의 그래프 노드 간 pairwise relation을 인코딩하는 graph Laplacian matrix의 extension 형태로써, simplicial complex에게 최적의 higher-order relations 까지도 인코딩하고 있는 generalized된 graph Laplacian matrix입니다. 즉, graph Laplacian 행렬은 Hodge Laplacian 행렬의 하나의 클래스로 생각해볼 수 있습니다.
  • 직관적으로, 노드 간 관계를 인코딩하는 행렬이기 때문에, 0-Hodge Laplacian matrix 꼴이라고 생각해볼 수 있겠습니다.
• 다음 행렬은 미분기하학의 Hodge Thoery (호지 이론) 을 따라 정의되며, 리만 매니폴드 (Riemannian manifold)의 (코)호몰로지 (Co-homology)에 기반을 두고 있습니다.
  • 정말 방대한 호지 이론의 하위 개념들 중에, 라플라스 연산자 및 호지 분해 (Hodge decomposition)에 대해 집중적으로 이해해봅니다.
  • 간략하게, 호지 라플라스 연산자는 n차원 리만 매니폴드 상의 미분 국소적 구조(수학 용어 : 층) 사이의 외미분 (d) 및 Transpose (d^T) 요소로부터 정의됩니다.
  • 호지 분해(Hodge Decomposition)는 라플라스 연산자를 기반으로 임의의 k차 미분 형식 꼴을 3가지 고유 성질들로 유일하게 분해할 수 있음을 보인, 호지 이론에서 중요한 개념 중 하나입니다.
• 위 개념을 기반으로 (k-th combinatorial) Hodge Laplacian matrix (L_k)는 Boundary operator (B_k) 및 adjoint (B_k^T)의 조합 꼴로 다음과 같이 정의됩니다.

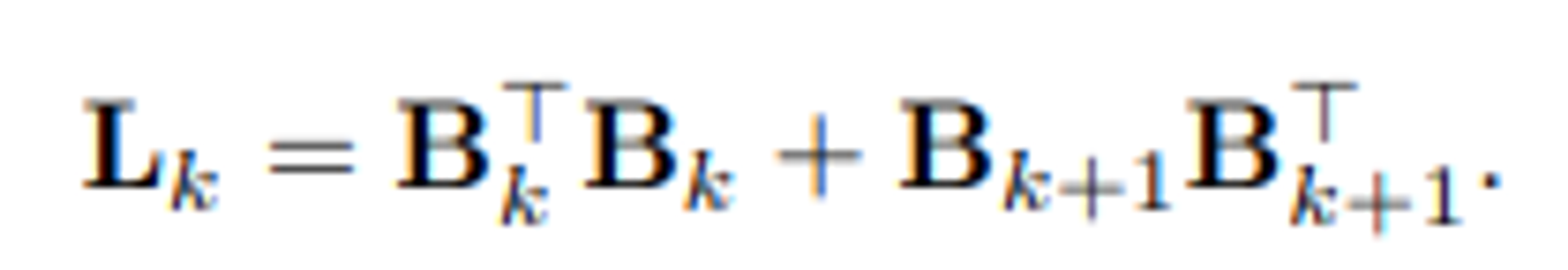
• graph Laplacian (L_0) = B_1 * B_1^T := B_0 = 0 을 만족합니다.
• Boundary operator의 정의를 다음 식에 적용하여 생각해본다면, formal term은 직관적으로 (k-1)-simplex와 k-simplex 사이의 신호 흐름을 나타내고 있으며, latter term은 k-simplex와 (k+1)-simplex 사이의 신호 흐름을 나타내고 있음을 암시해볼 수 있습니다.
• 다음 Hodge Laplacian에 대한 자세한 Algebraic Analysis 및 Proof는 다음 논문을 참고해보시면 정말 좋을 것 같습니다 !
• 실제 대다수 어플리케이션 네트워크 (e.g. transporttion, supply networks, information network etc..)는 주로 엣지 상에서 정의되는 신호에 접근하여 실용적인 포인트를 추출합니다. 이러한 사실을 착안하여 simplicial complex 상에서 전달되는 신호 흐름의 해석은 일반적으로 Edge flow (1-simplex)를 대상으로 수행됩니다. 즉, 1-Hodge Laplacian (L_1)에 초점을 두고 있습니다.
  • 즉, 1-Hodge Laplacian은 엣지 신호들을 분석하고 해석하기 위한 최적의 shift-operator로써 선택될 수 있습니다.

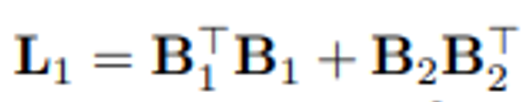
• graph Laplacian matrix와 유사하게 다음 1-Hodge Laplacian (L_1) 또한 positive semi-definite하기 때문에, 행렬의 고유분해 연산을 통해 얻어지는 음이 아닌 고유값의 주파수 성분 (frequency) 및 그에 대응하는 고유벡터의 기저로부터 신호의 부드러움 (Smoothness)을 정의할 수 있습니다. 다음 연산을 통해 전적으로 해당 Simplicial complex의 엣지 상에서 정의되는 신호의 모든 정보에 접근할 수 있다고 볼 수 있겠습니다.
• 호지 분해 개념을 가지고 와서, k-simplex 신호가 존재하는 Eigenspace을 3가지 직교 하위공간 (orthogonal subspaces)로 나누어 분석해볼 수 있습니다. 다음 공간은 1-Hodge Laplacian의 고유벡터들로부터 스팬(span)됩니다.

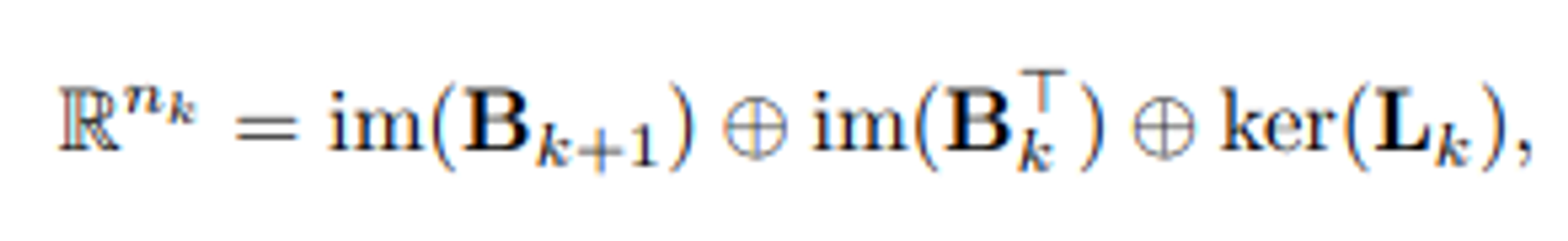
• im( ), ker( ) : 해당 행렬의 image & kernel space를 의미합니다.
• +기호 : 직교 공간들의 합병 연산을 의미합니다.
• n_k : 해당 신호가 놓인 실수 공간의 차원으로, k-simplex의 cardinality와 동일합니다.
  • k=1의 경우, n_1은 엣지 요소들의 총 개수와 동일합니다.
  • E.g. for a sample k-simplex := ({1}, {2}, {3}, {1,2}, {2,3}, {1,2,3}), n_1 = 2 ({1,2}, {2,3})
• Simplicial complex의 Edge flow 관련한 위의 호지 분해 공식은 구체적으로 "Free-module" Theory 개념을 기반으로 파생된 개념입니다. 다음 자세한 내용은 글의 범위에서 벗어나기에.. 설명은 생략하지만 관심 있으신 독자분들께서는 다음 링크를 참고해주시기 바랍니다 !
• 분해된 각각의 직교 공간들은 명칭이 존재합니다. 위 공식의 항 순서대로 'Curl space', 'Gradient space', 그리고 'Harmonic space'라고 불리우며, 각 공간에서 해석될 수 있는 신호의 특성들 또한 서로 독립적입니다.
• 직관적으로 각각의 신호 공간에 대하여 해석해봅시다. (결국 맵핑 함수입니다.)
  • 기준 신호 (f)로 생각하고 있는 엣지에 대하여 (k=1),
    • Gradient space = im(B_1^T) : 노드 -> 해당 엣지로 흘러가는 신호에 대한 정보를 내포하는 공간입니다. 다음 신호 흐름은 다른 potential value (or difference)을 갖는 두 노드를 연결하는 엣지를 기준으로, 해당 엣지에 흘러가는 gradient flow 혹은 potential flow가 존재하는 공간으로 해석할 수 있습니다.
      • Image space(=> {f = B_1^Tv} for all v in R^n_0)이기 때문에, 노드로부터 엣지 공간으로 사영 (project)되는 맵핑 함수로써 정의됩니다.
      • 노드 상에 존재하는 신호는 non-cycle하기 때문에, gradient space = non-cyclic space라고도 부릅니다.
    • Curl space = im(B_2) : 삼각형 -> 해당 엣지로 흘러가는 신호에 대한 정보를 내포하는 공간입니다. 구체적으로, 삼각형 면 상에서 cycle하는 신호가 해당 면을 구성하는 엣지 상으로 흘러가는 신호들이 맵핑되는 공간입니다.
      • 이러한 신호들의 흐름을 curl flow라고 부르며, 다음 신호들이 모여있는 curl space는 삼각형 (2-simplex)를 따라 local circulation하는 요소들의 선형결합 꼴로 정의되는 cyclic space입니다.
      • 마찬가지로 Image space(=> {f = B_2 t} for all t in R^n_2)이기 때문에 삼각형으로부터 엣지 공간으로 사영되는 맵핑 함수로써 정의됩니다.
    • Harmonic space = ker(L_1) : curl flow의 선형 결합으로 표현될 수 없는 global circulation (simplicial complex 상에 전체적으로 흘러가는 엣지 신호)을 나타내는 공간입니다. 즉, 위의 curl space와 orthogonal합니다.
      • ker(L_1 = B_1^TB_1 + B_2B_2^T)이기 때문에, 엣지로부터 노드 및 삼각형으로 흘러가는 신호들이 놓여있는 엣지 공간으로 정의됩니다.
      • Harmonic space 또한 cyclic space에 해당합니다.
  • 위의 space 개념을 한 눈에 볼 수 있도록, 아래 그림과 Fig 3을 참고해보시면 좋을 것 같습니다.

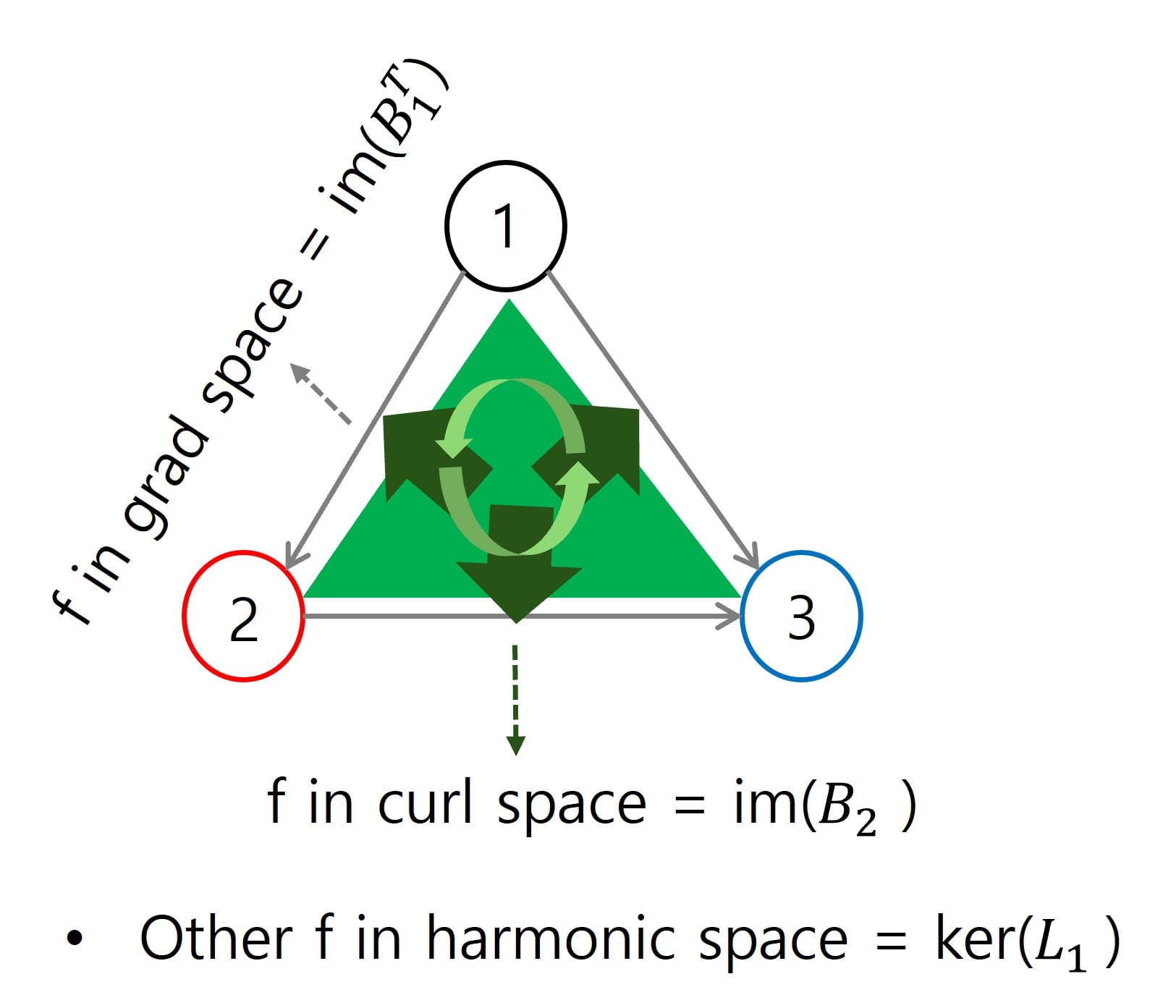
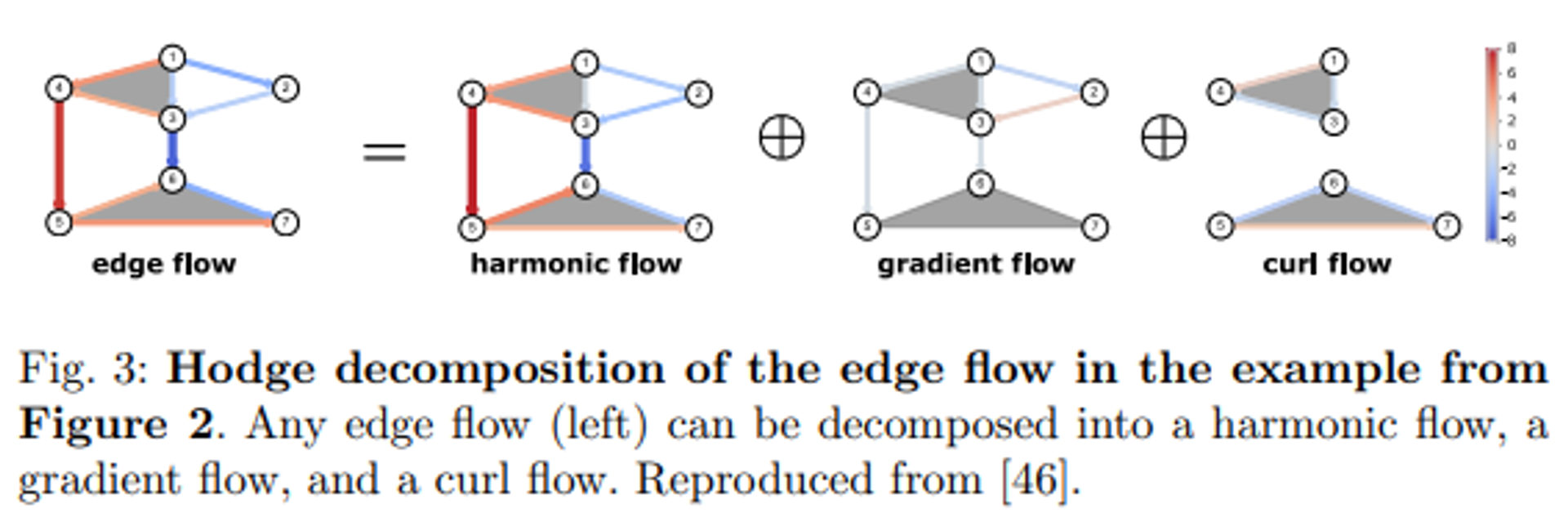
• 이번 주 오마카세는 Simplicial complex의 엣지 신호 상에서 정의되는 Hodge Laplacian 및 Hodge Decomposition에 대한 개념과 대수적 해석을 살펴보았습니다. 전체적인 TSP 도메인 상에서 정말 중요한 두 가지 개념인지라, 최대한 집중적으로 이번 주 오마카세에 담아보려 했습니다.
• 해석을 위한 수학적 배경 지식이 조금 요구되기도 하고, 다소 생소한 개념들이라 한번에 이해하시는 데 조금 어려움이 있을 것 같습니다. 하지만 직관적으로 생각해보신다면 어느정도는 쉽게 이해할 수 있는 개념들인 것 같고, 여러 어플리케이션 도메인에서 적용해볼 수 있는 새로운 인사이트도 정말 많을 것이라 생각합니다.
• 해당 논문에서는 마지막 챕터에서 다양한 Application에 대한 연구 사례 (Flow smoothing, denoising, Semi-supervised learning, Simplicial neural networks etc..)들을 소개하고 있습니다. 이와 관련한 내용은 다음 오마카세에서 전달해드릴 수 있도록 하겠습니다. 감사합니다 !

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn

Building The LinkedIn Knowledge Graph

원본 링크 : https://www.linkedin.com/blog/engineering/knowledge/building-the-linkedin-knowledge-graph

정이태

시장에서 GraphRAG에 대한 관심도가 높아짐에 따라, Graph 스키마 재료로써 활용하는 지식베이스 그리고 온톨로지가 어떻게 설계되는지 또한 많이들 궁금해하고 있습니다. 그래프 기술을 적극 활용하는 회사로 알려진 링크드인에서는 굉장히 오랜시간 지식그래프를 구축하기 위해 여러 노력을 기울여 왔는데요. 오늘은 링크드인에서 기계학습을 활용해 어떻게 데이터로부터 엔티티를 추출하고 이를 활용해 지식그래프를 구축하는지 다룬 포스팅을 가져와 이야기해보겠습니다.

지식베이스를 만드는 것은 크게 두 가지 형태로 구분이 되어 진행이 되어왔습니다. ‘사람’의 개입 여부로 사람이 직접 데이터에 주석을 달거나, 사람의 개입없이 정해진 알고리즘을 활용해 데이터마다 주석을 다는 방식으로 구분지을 수 있겠습니다.

그럼 이 지식베이스 구축을 위해 링크드인에서는 어떤 노력을 기울이고 있을까요? 여러 유저군들로 나눌 수 있겠네요. 멤버 , 리크루터 , 광고 홍보 마케터 그리고 회사 담당자들 으로 나누어 질 것으로 예상되네요. 이 유저군들 각각이 링크드인 플랫폼을 활용하는 목적이 다를 것이고, 그에 따라 발생하는 콘텐츠들이 달라질터이니 이 콘텐츠들마다 특성을 도출하는게 주된 과제가 될 것이며 많은 사용자가 발생할수록 분류해야하는 콘텐츠들이 많을테니 이 무수한 량의 데이터들을 원활하게 관리 및 분석하기 위한 엔지니어링이 첨가될 것임을 예상할 수 있습니다.

이를 위해, 링크드인에서는 머신러닝 방법론을 활용한 데이터 표준화 방식을 채택합니다. 엔티티간 위계 설계, 엔티티 관계 추론 , 데이터 비즈니스를 위한 데이터 표현 , 그래프 형태의 데이터에서의 인사이트 도출 그리고 새로이 추가되는 데이터들이 유의미한지를 판단하기 위한 데이터간 상호작용 검정과 같은 과업을 머신러닝 방법론으로 해결하고자 시도합니다.

Construction of entity taxonomy

entity 가 형성되는 과정 두 가지 1. organic , 2.auto-created 관점에 대해 서두에 언급하며, 1.Generate candidate , 2.Disambiguate entites , 3.De-duplicate entites , 4. Translate entites into other language 4가지 과정을 거치며 어떻게 엔티티가 설계되고 이에 따라 어떤 엔티티들이 풍부해지고 축소되는지에 대해 이야기합니다.

엔티티들의 특성이 내부에서 추출이 가능한지 외부에서 추출해야 하는지에 따라 분류체계를 나누어 Linkedin 지식그래프에 적용합니다. 내부 / 외부 구분에 대한 기준을 예로 들어보자면, 우선 내부 기준은 members, skills, companies, and industries 와 같이 ‘직업’에 대한 공통점을 기반으로 연관성이 있어 분류체계에 속한다라고 한다면, 외부 기준은 해당 기업의 logo , reveneue 그리고 URL 와 같이 feature extraction from text, data ingestion from search engine, data integration from external sources, and crowdsourcing-based methods, 등과 같은 방법론이 적용되어 메타를 개별적으로 추출해야할 때를 의미합니다.

최종적으로 추출된 entity의 신뢰성을 위해 human-verified , 기계 학습 방법론을 적용하여 confidence score 를 entity 의 특성으로 담아주고 관리합니다.

Inferring entity relationship

Entity 를 설계할 때 떠오르는 방식은 크게 두 가지 나눌 수 있습니다. 사용자가 특정 유저와의 메세지, 클릭등과 같은 직접적인 행동으로 표출하여 이를 Entity에 반영하는 Explicit 방식과 사용자가 프로필 입력과 같은 간접적인 행동 데이터를 분석해 잠재적인 , 추가적인 정보를 유추하여 Entity에 반영하는 Implicit 방식으로 나누어집니다.

이 두 가지 방식을 통해 설계된 entity 그리고 knowledge graph를 통해 해당 유저의 특성 메타가 형성됩니다. 메타는 job seeker, marketer 과 같은 분들이 광고를 집행하는 등의 Action 이 발생하기에 그 근거로써 활용되곤 합니다. 때문에, 링크드인 플랫폼 입장에서는 그 중요도가 상당하다 라고 할 수 있습니다. 이 중요도가 높은 정보에 오류가 발생하는 경우도 있는데요. 예를들어, 특정 유저가 자기가 다녔던 직장 정보에 대해 오타와 같은 실수를 통해 오기입하는 경우가 있기에 이를 탐지하고 정정해주어야 팔 필요가 있습니다. 이를 위해 기계학습 관점에서 binary classifier 를 학습하여, 이 에러를 사전에 방지하는 프로세스 또한 본 섹션에서 다룹니다.

Data representation

유저의 타이틀과 가지고 있는 직무 역량 이외에 잠재 직무역량 , 타이틀 등을 발견하고 이를 정제하기 위한 과정을 다룬 부분입니다. 타이틀과 직무 역량은 문자로 표현되어 유저가 기입하니, 이를 문자 관점으로 접근해 머신러닝을 활용한다 라는게 주된 골자인 섹션인데요. 간단합니다. 임베딩 모델을 활용해 문자들을 숫자 형태로 변환한 후, 이를 특정 차원으로 압축하여 해당 공간내에서 proximity 에 따라 그 유저의 잠재적인 특성들을 추가 발견한 뒤, 지식그래프를 설계할 때 발생하는 과업인 엔티티 위계 설정 및 엔티티 관계 유추때 활용합니다.

아래 그림 예시를 보면, ‘Web Developer’라는 title 근방에 iPhone, Firefox , symfony , HTML Scripting 과 같은 top-k를 설정하고 이에 따라 11시 방향의 지식그래프 스키마를 구축하는데 data 가 채워진다 라고 봐주시면 좋을 것 같습니다.

Insights extraction from the graph

집계성 분석을 통해 1차 통계 인사이트를 도출하고 이를 어떻게 지식그래프 형성 및 정교화에 도움이 되는지를 다룬 부분입니다. 구인 구직을 위해 필요한 직무 역량을 집계하여 1차적으로 분포를 확인한 뒤, 이에 따라 새로운 데이터 발생시 이 데이터가 어떻게 엔티티로 표현되어 지식그래프에 담기는지를 이야기합니다. 아래 그래프 스키마를 예로 들어 설명해보겠습니다. 스킬 이라는 노드를 가운데 두고 member , job 이라는 노드들이 관계가 형성되어 있는 그래프입니다.

동일한 member 노드라고 하더라도, 실선과 점선으로 표현하여 구분되어 있듯이, 이미 그 스킬을 가지고 있는 사람, 가지고 있지 않으나 배우길 희망하는 사람으로 나누어져 이 엔티티간 구분을 할 수 있게 됩니다. 이처럼, 특정 기업에서 요구하는 직무 역량을 1차적으로 통계로 도출해보고, 그에 따라 대표적인 skill 노드를 만들어 연결해준뒤, 유저의 프로필 그리고 플랫폼 내에서 유저의 행동 패턴을 분석하여 새로운 데이터가 발생할 시 이에 따라 연결이 형성되게끔 유도함으로써 데이터 표준화와 지식그래프 구축을 함께하여 비즈니스를 위한 양질의 데이터를 얻게됩니다.

이번 게시물에서는 지식그래프를 설계하기 위해서 링크드인 플랫폼에서 어떤 순서와 모듈 설계를 활용했는지에 대해 알아보았습니다. 분류 체계를 만들고, Entity를 정교화하기 위해 Explicit , Implicit 관점으로 접근 그리고 이를 임베딩 공간에 맵핑하여 잠재적인 관계까지 유추하기 위한 추가 보완과정까지를 거쳐 도출된 Entity들을 활용한 지식그래프까지 되게 간단해보이긴하나, 요즘같이 복잡한 방법론들을 적용하기 위해 필요한 도입비용 대비 간단하고 효용성이 높아보이는 본 포스팅의 방법론이 훨씬 좋은 접근방법론으로써 활용되지 않을까 싶네요. 회사의 데이터를 통합해 지식그래프를 구축하고자 하시는 분들에게 추천드리는 포스팅입니다.