24년 11월 1주차 그래프 오마카세

Generalized Simplicial Attention Neural Networks (1)

paper link : https://arxiv.org/abs/2309.02138

official code : https://github.com/luciatesta97/Generalized-Simplicial-Attention-Neural-Networks?utm_source=catalyzex.com

• 저번 주 오마카세에서는 데이터 상에 내재하는 다양한 토폴로지 표현 (e.g. Simplicial-, Cell-complex)들을 일반화할 수 있는 Combinatorial complex의 TDL 기반 모델, GCCNs의 구조 및 아이디어를 살펴보았습니다.
• 이번 주 오마카세에서는 토폴로지 표현 상에 내재하는 신호들을 처리하는 TSP (Topological Signal Processing) 도메인에서의 일반화된 신경망 아키텍처를 제안하는 논문을 소개해드리고자 합니다. 논문 제목에서부터 알 수 있듯이, 어텐션 메커니즘을 기반으로 Simplicial complex 표현 상의 내재하는 신호들을 다루는 모델로 생각됩니다.
  • TSP 기반 Simplicial attention networks의 사전 연구가 존재합니다. 정확하게는 다음 모델 아키텍처 (사전 연구 논문의 Fig 1, 식 18 참고)의 일반화 형태로 생각할 수 있습니다.
• Simplicial complex 상의 신호를 처리하는 방법에 대해서 이전 오마카세 글에서도 몇번 다루어본 적이 있었습니다. 구체적으로, 7월 3주차 ~ 8월 1주차 동안 3번에 걸친 'Signal processing on Simplicial Complexes' 이름의 오마카세 글을 통해 전달해드렸었습니다.
• 최근 저희 GUG 커뮤니티에 들어오신 분들을 위해 본 논문에서의 설명(II. Background on Topological Signal Processing)을 참고하여 가볍게 Recap해본 이후, 핵심 아이디어를 살펴보도록 하겠습니다.
  • 전체적으로 다루어드릴 중요한 내용들이 꽤나 방대하다고 생각되어, 다음 주 오마카세까지 해서 2차분의 연재로 나누어 전달해드릴 계획입니다.
  • 이번 주 오마카세는 Recaps + (Extended) Simplicial complex filters의 세션 내용들로 구성되었으며, 다음 주 오마카세는 Generalized Simplicial Attention Networks (GSANs)의 백본모델인 Generalized Simplicial Convolutional Networks (GSCNNs)과 핵심 모듈인 Simplicial complex Attention Layer의 내용들로 구성될 예정입니다.

Signal processing on Simplicial complexes

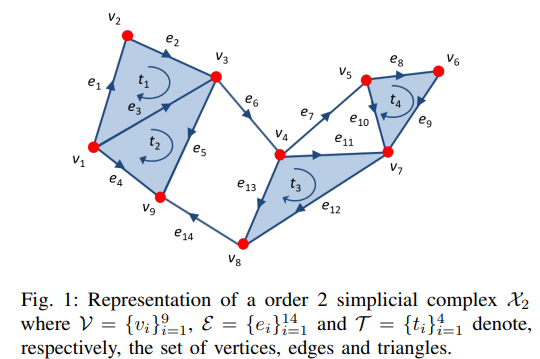
• TSP 도메인은 그래프 이론 및 신호처리 이론을 기반으로 발전해온 GSP (Graph Signal Processing)의 고차원 복합 컴플렉스로의 확장 분야로 생각해보면 좋을 것 같습니다.
• Fig 1와 같이, Simplicial complex 구조의 그래프 상에는 크게 3가지 요소들이 존재합니다. 노드, 엣지, 그리고 그들로부터 이루어지는 면이 있습니다. 그리고 엣지 및 면 상에는 화살표로 표기되어 있는 방향성 (Orientation) 정보 또한 존재합니다.
  • 기존 GSP에서는 노드 혹은 엣지만의 신호를 처리하는 데 집중되어있는 반면에, TSP에서는 노드(0-Simplices), 엣지(1-Simplices), 그리고 면(2-Simplices) 모든 요소들 상에 내재하는 신호들의 관계성을 한번에 처리합니다. 그러한 부분에서 TSP는 GSP의 확장 버전으로 생각해볼 수 있을 것 같습니다.
• 차원이 다른 (k=0,1,2) 복합 컴플렉스 요소들의 신호를 어떻게 한번에 처리할 수 있을까요? 그 핵심은 바로 Simplicial complex 형성 조건인 Incidence relation으로부터 정의되는 (Co-)Face 및 Boundary matrices와, 호지 이론(Hodge Theory)의 호지 라플라스 연산자 (Hodge-Laplacian operators) 및 그 연산자의 호지 분해 (Hodge-decomposition) 연산입니다.
  • 위의 Bold체로 표기한 개념들 정도만 알아두셔도 충분히 Simplicial complex 상의 TSP 기법들을 이해하는 것은 어렵지 않을 것으로 생각합니다. 다음 개념들을 자세하게 다시금 설명드리는 것은 생략하고 해당 논문의 설명으로 가볍게 Recaps 해보도록 합시다. (자세한 설명은 오마카세 7월 3주차~8월 1주차 설명을 참고해주시기 바랍니다.)
  • k-simplicial signal은 컴플렉스 상의 모든 k-simplices (노드, 엣지, 면 등)를 실수 공간으로 맵핑하는 일종의 임베딩 함수 집합으로 정의됩니다. 구체적으로는 식 1의 신호 집합들을 최대 K차수만큼 Concatenate하여 식 2와 같이 얻어냅니다.

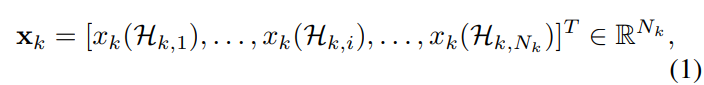
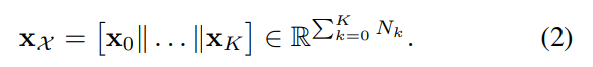
• 엣지 신호를 집중적으로 다루는 TSP 주요 타겟의 일반성을 유지하기 위해, k=1의 경우를 살펴보면 다음 신호들은 x_0,1,2 (각각은 노드, 엣지, 면의 신호들에 해당)의 임베딩 함수들의 집합 꼴로 생각해볼 수 있겠습니다.

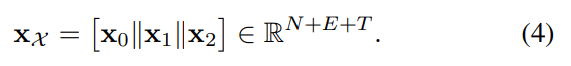
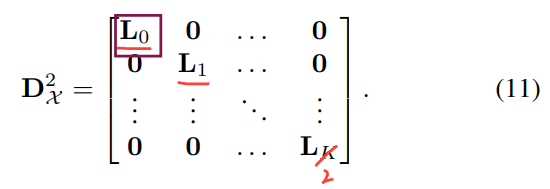
• 식 4의 해당 Simplicial complex signal에 대하여, Incidence relation (일종의 Neighborhood in complex) 및 Orientation 정보를 한번에 인코딩하는 Boundary matrix는 식 5와 같이 정의되며, 다음 matrix를 기반으로 Hodge Laplacian matrices를 식 6~8로 정의합니다.

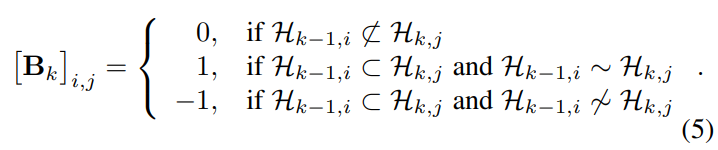
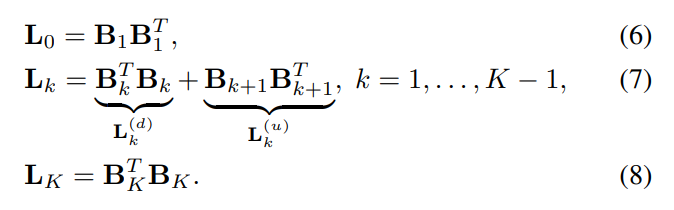
• 정의된 Hodge Laplacian matrices을 기반으로 Hodge decomposition 연산을 수행하여 3가지 독립적인 토폴로지 스펙트럼 공간 상에서 근접 차수 요소들(e.g. 0 & 1-simplices / 1 & 2-simplicies) 간의 신호 관계성을 인코딩합니다.

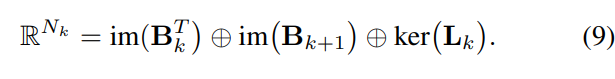
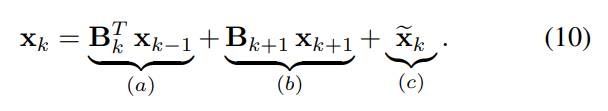
• 엣지 신호 (k=1)를 고려하였을 때, 식 9의 각 스펙트럼 공간들은 식 10의 해당 신호 요소들의 특성에 따른 명칭을 가지고 있으며 구체적으로 Gradient (with irrotational component, (a) 부분) & Curl (with solenoidal component, (b) 부분) & Harmonic space (with harmonice component, (c) 부분) 라고 칭합니다.
• 다음 공간에서 해석할 수 있는 자세한 스펙트럼 특성들은 생략하겠습니다. 본 논문의 설명 혹은 이전 오마카세 글들을 참고해주세요.
• Hodge Laplacian operators는 Simplicial complex의 근접 차수 간 신호적 관계를 포착하는 데 적합한 연산자로 알려져있으며, 그로부터 TSP 도메인에서 널리 사용되고 있습니다. 하지만, 본 논문의 저자들은 근접 차수만 고려하는 것보다 그 이상의 차수 정보를 한번에 포착할 수 있는 연산자를 활용하고자 합니다.
• 따라서 저자들은 Hodge Laplacian operator가 아닌 Dirac operator를 활용하기로 결정합니다. 식 12로써 정의되는 Dirac operator의 특성은 Dual boundary matrices (B₁ & B₂)를 한번에 사용하는 사실로부터 직관적으로 1차 이상의 정보를 한번에 포착할 수 있음을 이해할 수 있겠습니다.

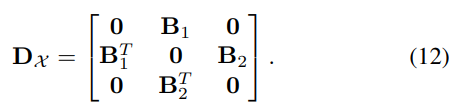
• 재밌는 사실로는 Hodge-Laplacian operator와 마찬가지로 Dirac operator 역시 Decomposition 함으로써 두가지 하위 연산자들의 독립적인 스펙트럼 공간으로부터 신호 해석을 할 수 있다는 점입니다.
  • 다음 Dirac decomposition 관련한 설명은 다음 논문을 참고해주시기 바랍니다.

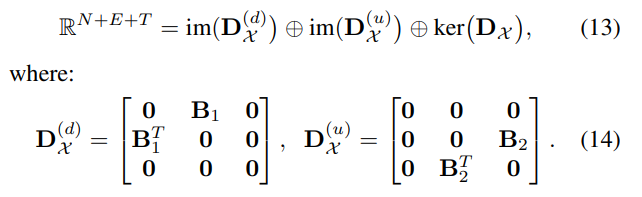
Extended Simplicial complex filters

• Dirac operators 및 Decomposition 연산으로부터 정의되는 Simplicial complex filters (식 15)는 기존의 Hodge-Laplacian operators 및 Decomposition 연산으로부터의 fitlers를 좀 더 확장시킬 수 있습니다.

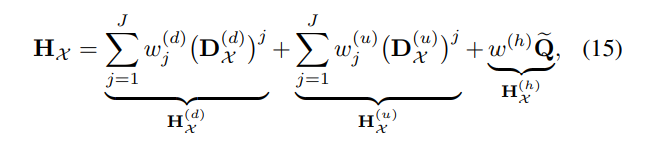
• 식 14와 15를 비교해보면, H^(d) 부분은 lower neighborhoods를 만족하는 요소 상의 신호들을 집계하며 H^(u) 부분은 upper neighborhoods의 경우를, 그리고 H^(h)은 앞의 신호들과 독립적인 Harmonic signal을 집계하는 부분으로 해석해볼 수 있습니다.
• 여기에서 Q 행렬은 Harmonic signal의 독립적 속성을 장담하기 위한 Block diagonal matrix로써 아래의 식 16과 같이 정의됩니다.

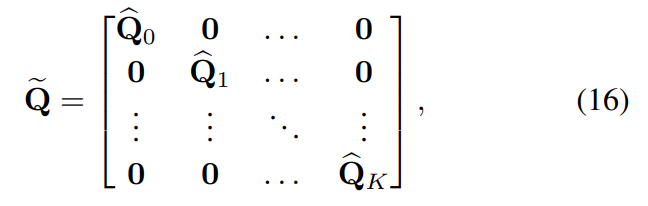
• 행렬 안의 {\hat_Q}은 harmonic embedding functions의 집합으로써 harmonic space로의 해당 신호를 맵핑하는 역할을 수행합니다. 하지만 이러한 형태로부터 얻어지는 Q의 Dense matrix 꼴을 연산적 효율성 측면에서 Sparse하게 만들어주기 위해 식 17과 같이 approximation하여 사용한다고 본 논문에서 언급합니다.

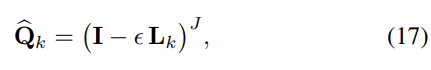
• 식 15로부터 정의된 (extended) Simplicial complex filters를 기반으로 Simplicial complex의 노드, 엣지, 면 상의 신호들을 필터링하는 연산은 최종적으로 식 18과 같이 나타낼 수 있습니다.

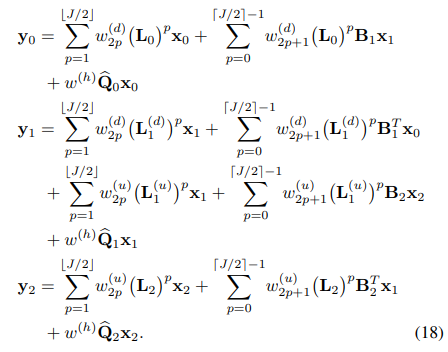
• 출력 신호 (y)가 어떠한 방식으로 입력 신호들을 집계하여 계산되는 지에 주요 초점을 맞추어 살펴봅시다. 모든 요소들의 신호 상에서 동일한 과정으로 진행되기 때문에, 여기에서는 노드 신호에 대해서만 살펴보도록 하겠습니다.
  • 출력 노드신호 (y_0)는 lower neighborhoods 관계를 만족하는 입력 노드신호 (x_0) 및 upper neighborhoods 관계를 만족하는 연결 엣지신호 (x_1)을 받아 각 Gradient & Curl & Harmonic space 상에서 shift operator (L_0)과의 weighted Linear combination 연산을 통해 구해집니다.

• 여기에서 필터 크기의 exponential growth를 방지하기 위한 특별한 테크닉이 포함되어 있으며, 식에서 보시는 것과 같이 H^{(u, d)}의 항에만 적용되어 있습니다.
  • 구체적으로, 최대차수 J/2까지의 x_0의 짝수 인덱스(2p)에 대해서만 (재귀적인) 필터링 연산이 진행되도록, x_1에 대한 필터링 연산은 최소 차수 J/2 - 1부터 홀수 인덱스(2p+1)에 대하여 진행되도록 설계하였습니다.
  • 또한 가중치 w_2p^(d), w_2p+1^(d)는 p차 shift operator에 대하여 공유되기 때문에 연산적 이득을 취할 수 있음을 명확하게 알 수 있습니다.

• 이번 주 오마카세에서는 Simplicial Attention networks의 TSP 기반 일반화된 모델 아키텍처를 이해하기 위한 배경지식 및 Extended Simplicial filters의 개념에 대해 전달해드렸습니다. 간략하게 전체 내용을 요약해보면,
  • Simplicial complex의 복합 컴플렉스 상의 신호들을 한번에 집계하기 위해, 기존 방법들은 Hodge-Laplacian operator 및 Decomposition 연산을 활용하여 근접 차수 간의 관계성을 포착하는 방식으로 필터를 설계하였습니다.
  • 다음 논문에서는 근접 차수들 간의 관계만 고려하는 것 이상으로 고차수 간의 직접적인 관계까지도 한번에 고려하기 위한 아이디어를 기반으로 Dirac operators 및 Decomposition 연산으로 기존 방법을 확장하여 Extended Simplicial complex filters를 설계하는 방법을 제안하였습니다.
• 오마카세 상에서 설계 과정에 대한 구체적인 설명 및 디스커션 등을 최대한 배제하고, 직관적으로 해석해볼 수 있는 설명을 기반으로 구성해보았습니다. 관심 있으신 독자 여러분들께서 보다 정확한 이해를 위해 해당 논문을 읽어보시는 것을 추천드립니다.

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn