GraphOmakase

24년 11월 2주차 그래프 오마카세

[AD]GUG 6번째 세미나

안녕하세요 GUG 입니다.

연말이라 그런지, 여기저기 서밋 컨퍼런스들이 많이 열리고 있네요! 이 흐름을 타서 GUG또한 세미나를 개최합니다.

이번 행사는 감사하게도 SKT Devocean에서 공간후원을 해주셨어요. 역시 국내 개발자 생태계를 위해 아낌없이 지원을 해주는 좋은 플랫폼! 데보션 ! GraphRAG와 그래프의 뼈대가 되는 온톨로지가 이번 행사 주제입니다. 다음에 해당되는 분들에게 특히나 도움되지 않을까 하는데요.

GraphRAG 구축은 했으나, 원하는 성능이 나오지 않아서 data driven 방식 및 개선에 대해 고민이신분
사내 메타데이터 통합 및 온톨로지 구축 및 평가에 대해 고민이신분
온톨로지는 구축했으나 어떻게 응용할지 고민이신분

요즘 생성형 AI에 RAG를 접목하는 과정에서 많은 분들이 겪고 계신 정보 분절 문제를 해결하기 위한 대안으로 Graph가 주목받고 있는데요. GraphRAG의 성공적인 구현을 위해서는 품질 높은 온톨로지가 중요한 기반이 됩니다.

이번 행사에서는 이러한 고민을 함께 나누고 해결 방안을 모색하고자 합니다. 관심 있는 분들의 많은 참여 부탁드립니다!

행사 신청 링크 : https://lu.ma/q3i93mpv

지난 행사들 : https://www.graphusergroup.com/graphtalks/

Generalized Simplicial Attention Neural Networks (2)

paper link : https://arxiv.org/abs/2309.02138

official code : https://github.com/luciatesta97/Generalized-Simplicial-Attention-Neural-Networks?utm_source=catalyzex.com

Index

Generalized Simplicial Convolutional Networks (GSCCN)
Generalized Simplicial Attention Neural Networks (GSANs) --> Simplicial complex attention layer, Properties
Hodge-aware Simplicial Attention Neural Networks (GSAN-Hodge)

저번 주 오마카세에서는 Simplicial complex의 기본 TSP 개념들과 근접 차수 이상의 관계성을 한번에 포착하기 위한 Dirac operator 및 Decomposition을 활용한 Simplicial complex filters을 전달해드렸습니다. 이번 오마카세로 전달해드릴 내용의 이해를 위해 반드시 짚고 넘어가야 하는 부분인 만큼 세션을 나누어 전달드리게 된 점 양해 부탁드립니다.
이번 주 오마카세에서는 다음 논문에서 제안하는 Generalized Simplicial Attention Neural Networks (GSANs)의 Base가 되는 GSCCN 모델 및 GSANs 아키텍처 그리고 핵심 특성들을 하나하나 자세히 살펴보겠습니다. 또한 추가적으로 기존 Hodge-aware methodology까지 활용할 수 있는 통합 모델 아키텍처인 GSAN-Hodge 구조까지 함께 살펴보도록 하겠습니다.

Generalized Simplicial Convolutional Networks

이름 그대로 Generalized Simplicial Convolutional Networks는 사전 연구였던 Simplicial Convolutional Networks (SCNs)의 일반화 아키텍처로 생각해볼 수 있습니다.
- 사전 연구의 SCNs 레이어 구조를 살펴보면 아래와 같습니다.

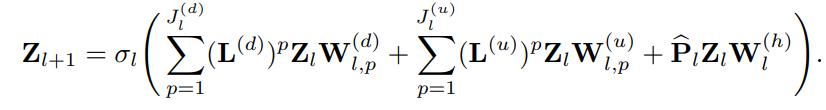
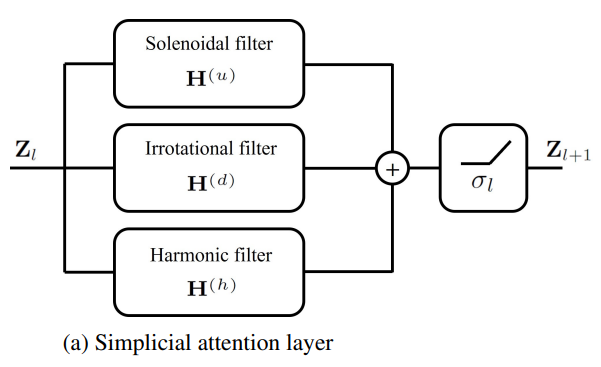
The output edge signals of the l-th layer (matrix form) in SCNs.

간략하게 Hodge-토폴로지 요소 간 lower (^(d) 표기) & upper (^(u)표기) neighborhoods 그리고 sparse approximated projector (hat_P)를 통한 harmonic component까지 고려하여 한번에 집계하는 형태로 볼 수 있습니다. 다음 설명을 해당 논문에서는 아래와 같이 설명하고 있습니다.

💡

The layer in (11) can be clearly interpreted as the aggregation of three filtering branches, one for irrotational components (based on lower neighborhoods), one for solenoidal components (based on upper neighborhoods), and one for the harmonic component.

SCNs는 근접 차수 간의 upper & lower neighbors' signals을 중심으로 위의 식을 따라 집계 및 업데이트가 진행됩니다. 하지만, 저자들은 그 이상의 신호 집계를 한번에 가능하게 하는 아이디어를 기반하여 GSCCNs 아키텍처로 일반화하기를 원합니다.
따라서, Extended simplicial complex filters를 활용하여 아래와 같이 Generalized Simplicial Convolution Layer를 정의합니다. 여기에서는 엣지 신호 중심(k=1)의 레이어 구조만 살펴보도록 하겠습니다.

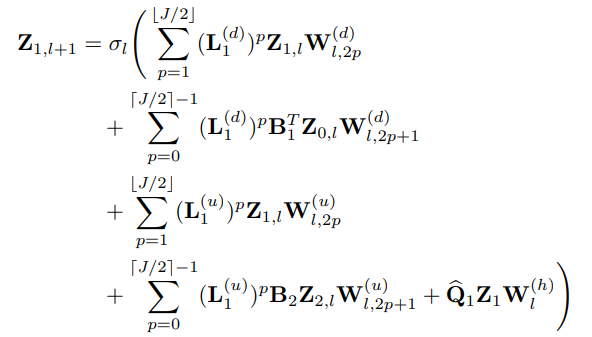
Edge signal(k=1) convolution via extended simplicial filters

구체적으로 다음 식의 1,2번째줄은 Dirac operator의 L₁을 shift operator로 활용하여 lower neighborhoods 조건을 만족하는 (L₁^(d)) 엣지 본인의 신호 정보와 (Z₁) 및 해당 노드들이 존재하는 공간 (im(B₁^T), Gradient space) 상으로 맵핑하여 노드 신호 정보(B₁^TZ₀, irrotational component)를 집계 받아옵니다.
마찬가지로, 3,4번째 줄은 동일한 shift operator을 활용하여 upper neighborhoods 조건을 만족하는 (L₁^(u)) 엣지 본인의 신호 정보와 해당 면 공간 (im(B₂), Curl space) 상으로 맵핑하여 면 신호 정보 (B₂Z₂, solenoidal component)를 집계 받아옵니다.
마지막 부분에서는 Sparse approximated projector (Q)를 활용하여 해당 엣지의 Harmonic component를 집계 받아옵니다.
모든 집계된 신호들을 합산하여 point-wise non-linearity 함수를 통과시켜 다음 레이어로 보내주는 구조입니다.
- Exponential growth filtering을 막기 위해 특정 필터 차수(J/2)까지의 짝(2p),홀수(2p+1) 인덱스를 나누어 가중치를 부여한 점 (각각 W_2p, W_2p+1)을 새로운 인사이트로 바라볼 수 있습니다.
- p번 재귀적으로 집계되는 동안 다음 가중치들이 공유되는, 즉 Weight-sharing 기법을 통해 연산 효율성을 가져옵니다.
Graph classification 등의 task에서는 마지막 레이어 이후 추가적인 Read-out layer를 추가할 수 있습니다.

Generalized Simplicial Attention Neural Networks (GSANs)

Simplicial complex attention layer

다음 GSCCNs의 구조를 기반으로 Self-attention mechanism을 추가하여 제안하는 GSANs 모델을 제안합니다.
핵심 아이디어는 데이터 상에 주어진 토폴로지에 맞추어 정의된 이웃들 전체에 masked self-attetion mechanism을 통해 해당 Simplicial complex에 가중치를 주는 Attention coefficients를 학습하는 것입니다.

💡

The core idea is to learn the coefficients of the weights of the diffusion over the complex via topology-aware masked self-attention, in order to optimally combine data over the neighborhoods defined by the underlying topology in a totally data-driven fashion.

다른 차수의 Simplices 요소들 간의 Attention을 계산해야하기 때문에, Anisotropic filtering operation으로써 바라볼 수 있겠습니다. 다음을 만족하는 대표적인 Topology-aware operators가 기존에 널리 사용되는 Hodge-Laplacian 이었는데요.
하지만, 다음 논문에서는 Hodge-Laplacian operator가 아닌 Dirac operator를 기반으로 모델을 설계하고 있었습니다. 그러한 사실로부터, 저자들은 더욱 일반적인 표기, Attentional shift operator, 를 아래와 같이 새롭게 정의합니다.

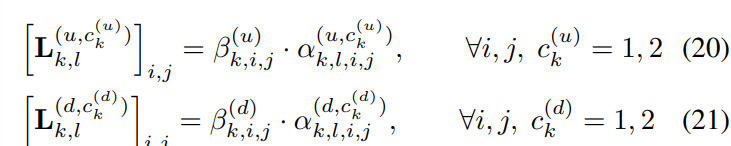
Masked attention coefficients in Attentional Shift Operators L_k^{(u&d, c)}.

식 20,21과 같이 해당 연산자의 요소에는 Normalized Attention coefficient (α)에 추가적인 요소 (c_k) 및 그 가중치 (β)를 포함하고 있습니다.
- 여기에서 c_k={1,2}는 Simplicial convolution 연산 가운데 shfit operator (L₁^{(d, u)})의 등장 횟수로 구해지는 인덱스입니다. 위의 'Edge signal(k=1) convolution via extended simplicial filters' 예시를 살펴보면 L₁^(d), L₁^(u)각각 2번씩 등장하였기 때문에 c₁^(u),c₁^(d) =2로 설정됩니다.
- β = {0, 1}는 일종의 indicator function으로써 해당 j번째 요소가 Upper & Lower neighborhoods의 조건을 만족하면 1, 아니면 0의 값을 갖습니다. 그로부터 Attentional shift operator의 요소를 masked attention coefficients라고 부릅니다.

다음 masked attention coefficients는 어떻게 학습되는 것일까요? 다음은 GSCCNs의 방법과 꽤 유사하게 진행됩니다. GSCCNs의 설명을 다시 빌려와서 먼저 엣지 입력 신호 (Z₁)에 대해 다음 과정을 살펴봅니다.

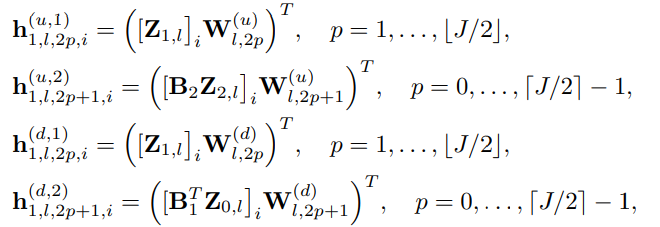
How to learn the masked attention coefficients

h₁^{(d&u, 1)}: 'Edge signal(k=1) convolution via extended simplicial filters'의 1,3번째 줄로부터, 본인의 정보만을 사용하기 때문에 c₁=1입니다. 해당 공유 가중치 행렬 W_2p^(d&u)를 사용하여 학습합니다.
h₁^{(d&u, 2)}: 'Edge signal(k=1) convolution via extended simplicial filters'의 2,4번째 줄로부터 c₁=2로 설정됩니다. 해당 공유 가중치 행렬 W_2p+1^(d&u)를 사용하여 학습합니다.
이렇게 학습된 신호들은 위의 특정 필터 차수까지의 조건에 맞추어 Concatenate됩니다. 그로부터 stacked vectors 꼴로 다음과 같이 표현될 수 있습니다.

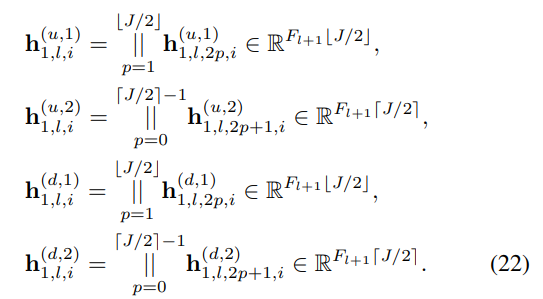
식 22로부터 Attention coefficients (γ)는 i, j번째 요소의 동일한 Upper & Lower 신호들을 받아 스칼라 계수를 반환하는 함수 꼴로 정의됩니다. 구체적으로 아래와 같이 Concatenate 및 LeakyReLU 비선형 함수를 활용하며, 각각을 Upper & Lower attention (γ^(u) , γ^(d)) mechanism으로 정의합니다.

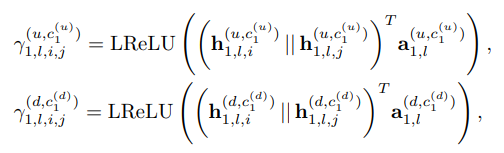
마지막으로 Normalized attention coefficient (α)는 softmax 함수를 사용하여 구해냅니다.
이 모든 것을 행렬 꼴로 식 28과 같이 정리하여 나타낼 수 있습니다.

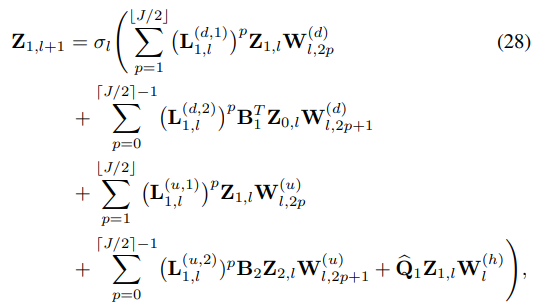
GSCNNs의 shift operator (L₁)로부터 Attnetion mechanism이 적용된 식 20,21의 Attentional shift operator (L₁^{(d&u, 1&2)})로 대체되었음을 쉽게 확인해볼 수 있습니다.
안정적인 self-attention 학습 프로세스를 위한 Multi-Head Attention 메커니즘도 쉽게 출력 신호들의 Horizontally concatenating 혹은 Averaging을 통해 구할 수 있습니다. (식 29, 30 참고)

다음 레이어의 동작 메커니즘을 Fig 2를 통해 한 눈에 알아볼 수 있습니다.

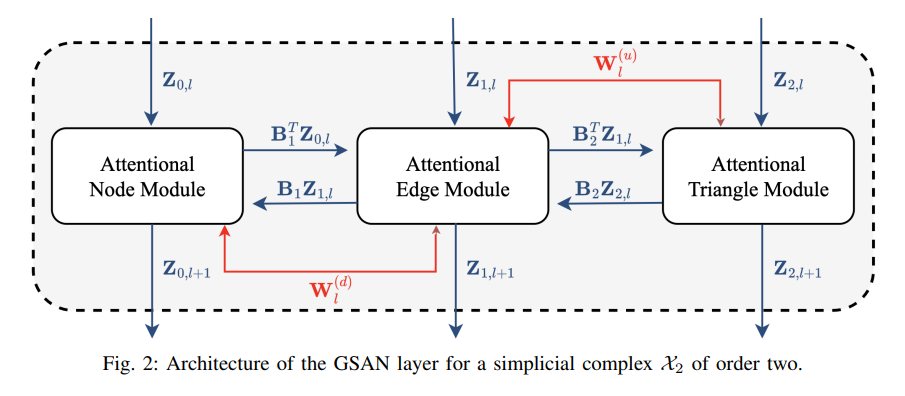
Satisfied Properties : Permutation equivariance, Simplicial awareness.

크게 2가지 특성을 만족함을 다음 논문에서 입증합니다. (Appendix A. 생략) 이러한 특성들로부터 쉽게 다른 Simplicial attention models을 일반화할 수 있으며, 더욱 효과적인 표현 결과를 얻어낼 수 있음을 설명합니다.

💡

These properties enable to learn more generalizable and efficient representation [52], [24], which are independent of the simplicial complex labeling and take advantage of the simplicial structure.

Specifically, we claim that the proposed GSAN architecture is permutation-equivariant and simplicial-awareness

식 28과 같이 GSAN layer에서 고려되는 모든 차수의 Simplices 요소들은 크게 B (boundary operator), Z (Signal), W (learnable parameters) 입니다.
Permutation-equivariance를 만족한다는 것은 한마디로 입력 신호 및 이웃 관계성에 대해 Permutation 연산을 수행하였을 때, GSAN layer의 전후 결과는 똑같음을 의미합니다.
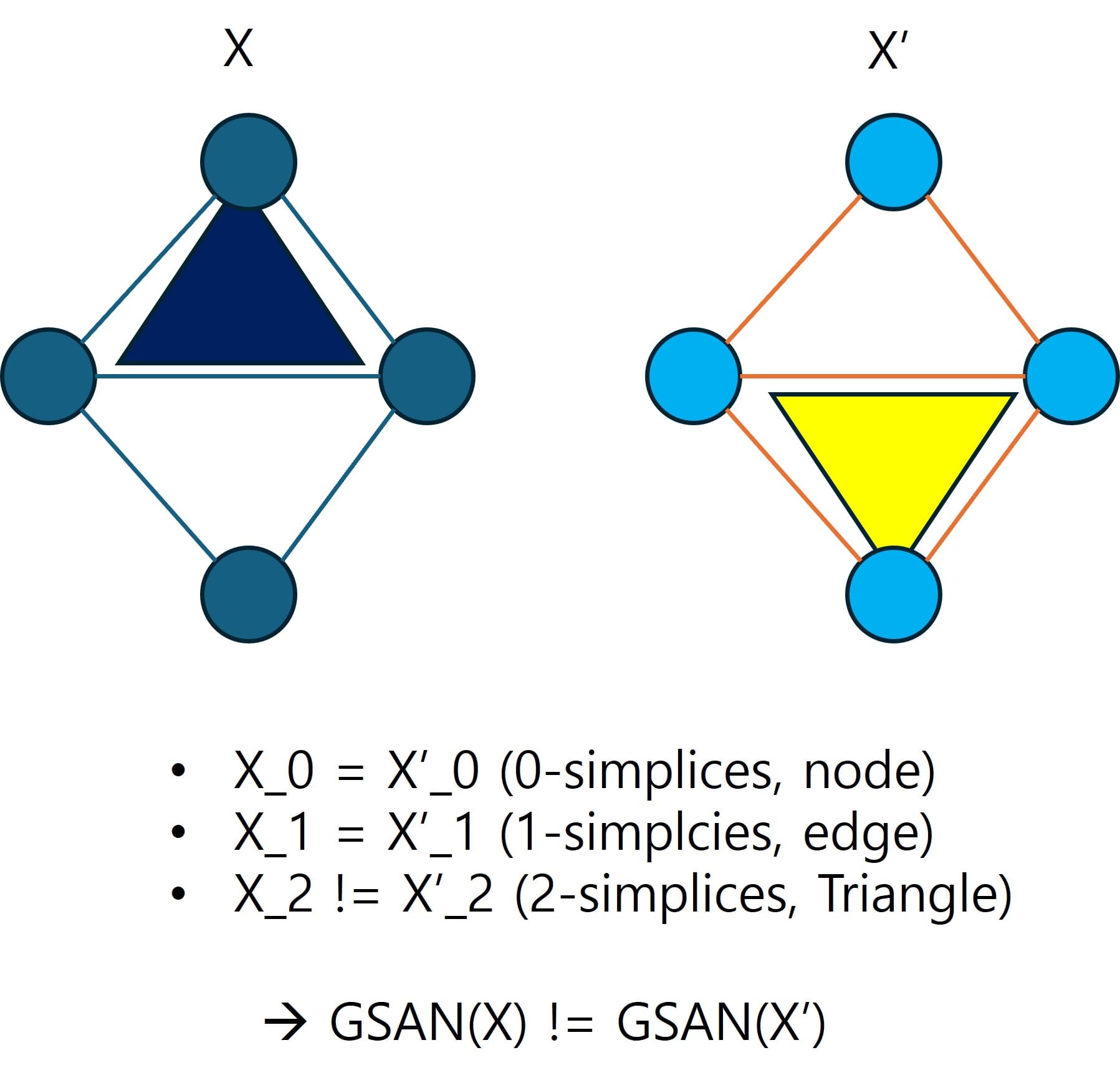
Simplicial-awareness를 만족한다는 것은 한마디로 최대 차수의 Simplices (k=1의 Simplicial complex의 경우 k=2의 Triangle가 해당)을 제외한 그 이하 차수의 Simplices 구조는 동일한 두 Simplicial complexes (X, X')가 존재할 때, 각각의 이웃관계성 차이로 인한 GSAN layer 출력 결과는 다르다는 것을 의미합니다.
- 후자의 경우, 이해가 안될 수 있기 때문에 아래와 같이 쉽게 그림으로 표현하였습니다.
- 후자의 사실로부터, Simplicial-awareness의 만족성 여부는 해당 Simplicial complex의 최대 차수 k-simplices에 많은 영향을 받는다는 사실을 알 수 있습니다.

Hodge-aware Simplicial Attention Neural Networks (GSAN-Hodge)

지금까지 설명드렸던 모든 내용들은 Dirac operator 및 Decomposition을 기반으로 두고 진행되었습니다.
저자들은 추가적으로 weighted Dirac operator를 기반으로 기존 방법들의 Hodge Laplacian의 유용한 특성들을 GSANs의 learned attentional operators으로 주입하고자 합니다. 이렇게 설계된 모델을 Hodge-aware Simplicial Attention Neural Networks (GSAN-Hodge)라고 부릅니다.
- 핵심 아이디어는 Metric tensor (G) 라고 불리우는 토폴로지 요소-가중치 행렬을 기반으로 (normalized) weighted incidence matrices를 활용하는 것입니다.

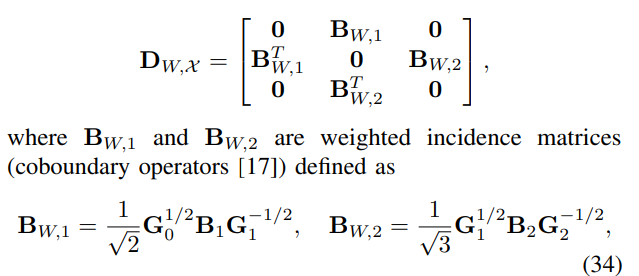
1-,2-simplices의 weighted incidence matrices를 식 (34)와 같이 정의하는데, 일종의 normalized graph Laplacian 형태와 비슷합니다. 다음은 Metric tensor이 항상 0이상의 요소들을 갖는 대각행렬의 형태를 장담할 수 있게 만들기 위합니다. 스펙트럼 그래프 이론 또는 ChebNet의 normalized graph Laplacian의 properties를 접목해 생각해보시면 쉽게 이해해볼 수 있습니다.

다음 weighted Dirac operator를 기반으로 weighted Hodge Laplacian을 정의합니다. 다음 weighted Hodge Laplacian도 마찬가지로 weighted Dirac operator의 제곱 행렬의 대각 요소에 위치하게 됩니다.

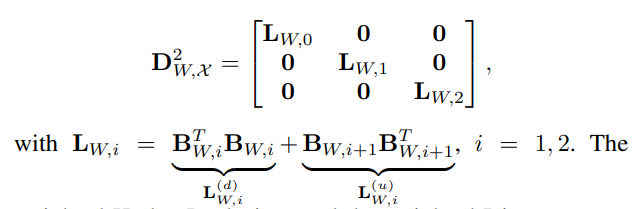
Weighted Hodge Laplacian (L_W,i) from the square of weighted Dirac operators (D²_W,X)

또한 weighted Dirac & Hodge Laplacian의 decomposition을 통한 독립적인 subspaces에서 각각의 스펙트럼 특성들을 추출할 수 있으며 그로부터 새롭게 weighted simplicial complex filters 및 연관 Layers를 설계할 수 있습니다. 다음은 앞서 설명드린 내용들과 동일한 방식으로 정의되기 때문에 자세한 설명은 생략하도록 하겠습니다.
실험 결과에서도 기존 Hodge Laplacian 기반 single-order signals을 적극 활용하는 Trajectory prediction (inductive learning) & missign data imputation (MDI, transductive learning) 분야 및 higher-order signals 또한 중요한 TUdataset graph classification 및 simplex prediction에서 관련 SOTA 모델들보다 향상된 성능 결과를 보여줍니다. 개인적으로 MDI에서 제안 GSAN의 Robustness한 성능 결과가 꽤 인상깊었습니다.

💡

In this work we presented GSANs, new neural architectures that process signals defined over simplicial complexes, performing anisotropic convolutional filtering over the different neighborhoods induced by the underlying topology via masked self-attention mechanisms.

GSANs are theoretically proved to be permutation equivariant and simplicial-aware.

Finally, we have shown how GSANs outperform current state-of-the-art architectures on several inductive and transductive benchmarks.

이번 오마카세에서는 제안 모델의 백본 GSCCNs의 구조와 그 위에 어텐션 메커니즘을 추가한 GSANs의 구조를 살펴보았습니다. 추가적으로 기존 Hodge Laplacian의 특성을 활용할 수 있는 GSAN-Hodge 모델까지도 전달해드렸습니다.
이런저런 많은 생소한 개념들이 많이 나와서 단번에 이해하기 어려운 논문이라 생각합니다. 한번 더 해당 논문의 핵심 아이디어를 요약해보자면, 다른 차수의 토폴로지 요소들을 한번에 활용할 수 있는 Dirac operator 정의 및 Decomposition으로부터 고유한 스펙트럼 특성들(Gradient, Curl, Harmonic)을 노드, 엣지, 면 상에서 어텐션 계수 학습을 통해 효율적으로 추출하는 것입니다. Fig 2의 flowchart을 통해 직관적으로 GSAN layer의 동작 메커니즘을 쉽게 이해할 수 있을 것으로 생각합니다.
추가적으로 그래프 상의 신호 분석에 항상 꼬리표처럼 따라붙는 Decomposition 과정에서 요구되는 막대한 연산량 문제를 해결하는 것이 중요하기 때문에, GSP에서는 polynomial approximated filters의 개념을 활용합니다. 하지만 TSP 도메인에서는 여전히 이러한 개선 방법들이 많이 소개되지 않아 활용 측면에서의 Scalabillity이라는 문제점이 항상 남아있었습니다.
다음 문제를 해당 논문에서는 Simplicial complex filters의 특정 차수 및 요소 인덱스를 분할하여 0-, 1-, 2-simplices 간의 신호 정보를 추출하는 독특한 테크닉을 추가한 부분 (식 18~19, 28)이 또 하나의 인사이트라고 생각됩니다.

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184