Sign in Subscribe
GraphOmakase

24년 12월 3주차 그래프 오마카세

Higher-order GNNs Meet Efficiency: Sparse Sobolev Graph Neural Networks

paper link : https://www.arxiv.org/pdf/2411.04570

official code : https://github.com/jhonygiraldo/S2-GNN?tab=readme-ov-file

  • 그래프 신경망의 주요 학습 메커니즘으로 사용되고 있는 메세지 전달 프로세스에 대해서는 모두들 잘 아시고 계실 겁니다. 주변 이웃 노드의 정보를 집계하여 자신의 정보를 업데이트하는 방식으로 진행되는데, 저 멀리 떨어진 이웃 노드의 정보를 집계하기 위해서는 인접 행렬의 거듭제곱을 수행해야 합니다. 그로부터 Higher-order relation 정보를 포착하기 위한 무거운 연산량을 요구하는 문제점도 잘 알려져있습니다.
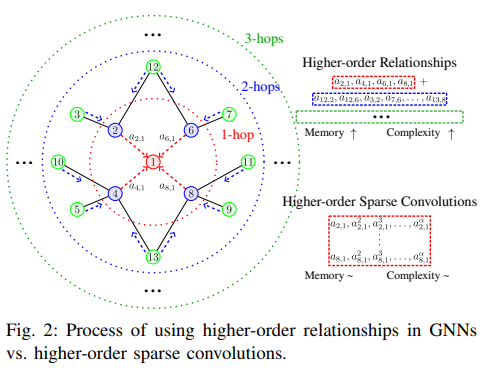
  • 그래프 스펙트럼 신경망에서 그 문제점은 더욱 부각됩니다. 왜냐하면 그래프 신호 처리(GSP)에서 Shift operator으로 널리 사용되는 그래프 라플라시안 행렬 기반 컨볼루션 연산 비용이 입력 그래프의 크기에 비례하여 증가하기 때문입니다.
    • 라플라시안 행렬의 고유분해를 통해 얻어진 고유벡터 행렬을 활용하여 그래프 푸리에 변환 (GFT)에 의한 입력 신호의 맵핑, 그리고 맵핑된 공간 상에서의 컨볼루션을 통한 특정 주파수 추출, 그리고 역 그래프 푸리에 변환 (IGFT)을 통한 필터링된 신호의 원래 공간으로의 맵핑 과정으로 진행됩니다.
    • 멀리 떨어진 노드의 신호를 포착하기 위해서는 다음 과정을 수십번 반복해야 합니다. 여기에서 라플라시안 행렬의 고유분해 비용이 그래프 크기에 따라 매우 비싸지기 때문에 (시간복잡도 O(n3), n: 노드 개수) 실제 그래프 데이터에 적용하기에는 확장성 및 효율성 측면에서 큰 한계점을 갖습니다. 또한 Transductive learning 관점에서 새로운 그래프 데이터에 대해 처음부터 다음 과정을 반복 수행해야 하기에 메모리 측면에서도 부담이 매우 큽니다.
    • 다음 문제를 완화하기 위해 대표적으로 Chebnet, GCN 등의 컨볼루션 방식에서는 다항식 근사화 (Polynomial approximation) 기법을 통해 이를 완화시켰습니다.

Sparse Sobolev Norm of Laplacian Matrix

  • 저자들은 위의 단일 라플라시안 행렬의 거듭제곱의 과정을 수십번 반복하여 업데이트된 그래프 상의 주파수 신호들은 해당 Shift operator 행렬의 단순 Hadamard product로도 동일한 주파수 신호들을 얻어낼 수 있다는 놀라운 사실을 발견하게 됩니다.
    • Hadamard product의 연산적 효율성은 보장되어 있기 때문에, 다음 사실이 맞다면 위의 취약점을 확실하게 보완할 수 있는 그래프 스펙트럼 컨볼루션 모델을 설계할 수 있게 될 것입니다.
💡
Relying on graph spectral theory, we make a fundamental observation: the regular and the Hadamard power of the Laplacian matrix behave similarly in the spectrum.
  • 여기서 핵심은 라플라시안 행렬 그 자체를 활용하는 것이 아닌, Sobolev norm Regularization term (L + εI)(ρ) 의 특성을 활용하여 대체 Shift operator로 정의하는 것입니다.
Sobolev Norm
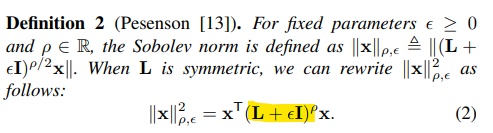
    • Sobolev norm 형태의 라플라시안 행렬 L(ρ)의 거듭제곱 연산을 통해 단순 라플라시안 행렬의 거듭제곱 Lρ 결과보다 더욱 다양한 주파수 요소를 활용할 수 있고, Better Condition number를 갖게 되면서 학습 과정에서 더욱 빠른 수렴율을 보장한다고 합니다. IV-A. Sobolev norm 설명을 참고하시기 바랍니다.
💡
The condition number κ(L) associated with the square matrix L is a measure of how well- or ill-conditioned is the inversion of L.
Better condition numbers are associated with faster convergence rates in gradient descent methods, as demonstrated in [14].
  • Sobolev Norm의 거듭제곱 연산은 Sparsity 측면에서 비효율적입니다. 따라서 Hadamard product 거듭제곱 꼴로 연산량을 효율적으로 낮춘 Sparse Sobolev term을 아래와 같이 정의합니다.
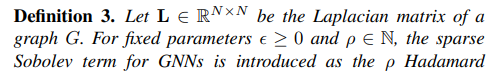
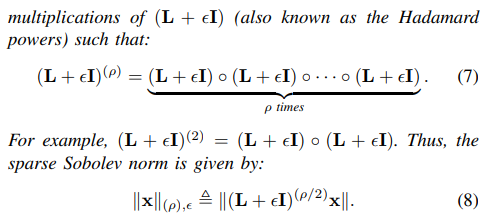
Sobolev norm의 ρ번 Hadamard product을 통해 Sparsity를 확보할 수 있음을 보입니다.
    • 여기에서 ρ가 자연수의 임의의 값에 대하여 행렬 곱셈을 Hadamard Product로 대체하였을 때, 동일한 Sparsity level을 유지할 수 있음을 보여줍니다. 아래의 Fig 3을 함께 참고해주시기 바랍니다.
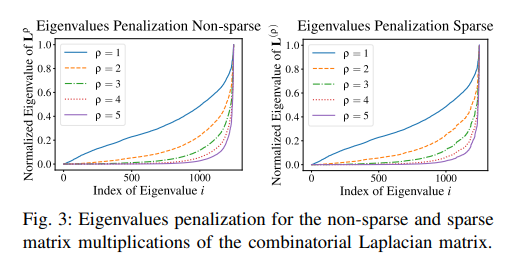
일반적인 normalized 라플라시안 행렬의 거듭제곱(왼쪽, non-sparse) 및 Sparse Sobolev norm 형태의 라플라시안 행렬의 거듭제곱 (오른쪽, sparse)의 주파수 결과가 매우 유사하다는 결과를 Fig 3에서 보여주고 있습니다.
  • 아래의 Theorem 2에서는 ρ=2의 식 10의 결과를 통해 Sparse Sobolev norm의 스펙트럼은 그래프 라플라시안의 고유벡터 및 고유값 행렬에 대한 Kronecker product 연산의 스펙트럼과 동치라는 인사이트를 제공합니다.

Sparse Sobolev Graph Neural Networks

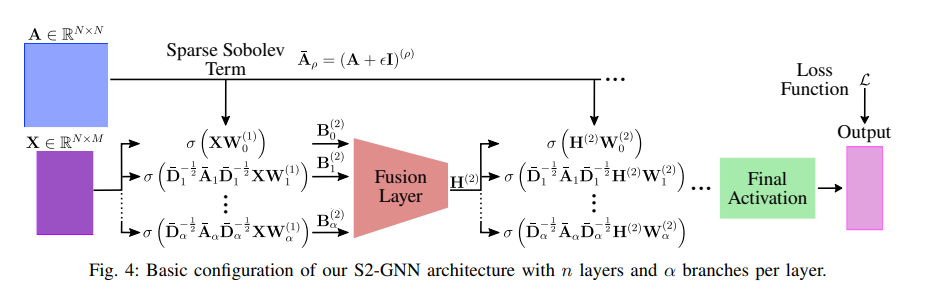
  • 위의 사실들을 기반으로 Sparse Sobolev GNNs (S2-GNNs) 모델 아키텍처를 설계하였습니다. 레이어 별로 α 브랜치에 따라 병렬적으로 그래프 컨볼루션을 수행하고 이들을 병합하는 심플한 구조를 확인해볼 수 있습니다. 실제 실험에서 α=6을 주었다고 합니다.
    • 보시다시피 신호 행렬 X에 대하여서는 GCN과 동일한 메커니즘으로 동작하지만 그 차이점은 Sparse Sobolev Term을 적용하는 부분 및 이들을 병합하는 Fusion Layer 정도로 보시면 되겠습니다.
    • Fusion Layer은 크게 Linear combination & MLP Fusion layer의 2가지 모듈로 구현되어 있으며, 주어진 데이터셋에 가장 적절한 최적화 알고리즘을 기반으로 결정됩니다.
    • 어텐션 메커니즘에 대해서 자세하게 설명되진 않았으나 쉽게 Sparse Sobolev Term에도 적용할 수 있다고 합니다.
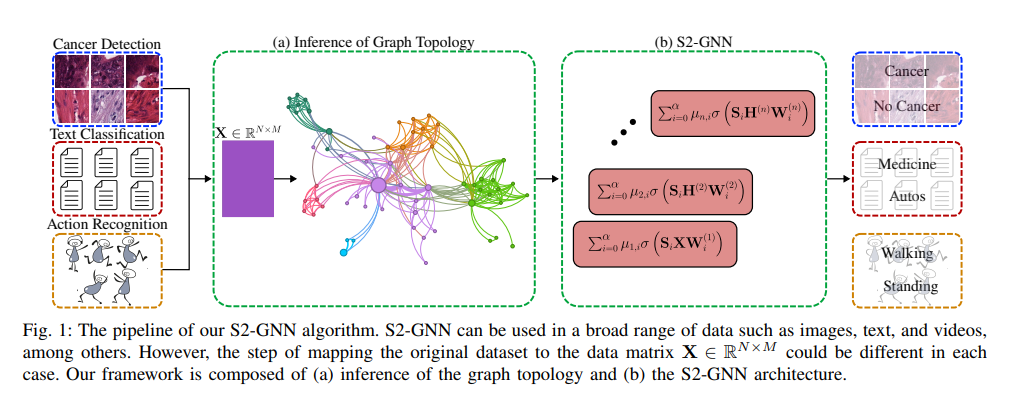
  • 전체 파이프라인을 보면, 다중 멀티모달 입력에 대해서도 해당 S2-GNN을 활용할 수 있다고 합니다. 주어진 데이터의 정확한 구조 정보가 존재하지 않더라도 단순 KNN 그래프 구조로 표현된 결과 상에서도 제안 모델의 강건한 성능을 보장할 수 있음을 Fig 1에서 간략하게 보여주고 있습니다. 모델 파라미터 선택에 관련한 Ablation 파트도 읽어보시면 좋을 것 같습니다.
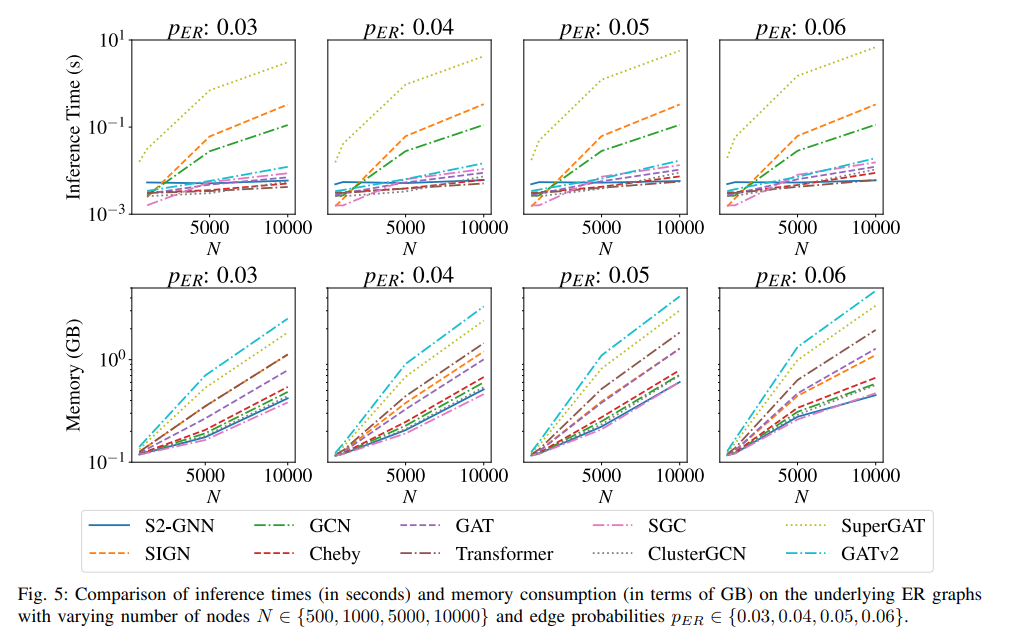
  • 해당 논문의 기여점인 연산량 및 메모리 효율성 부분을 보여주는 Fig 5의 결과를 통해, 다른 baseline models보다 더욱 빠른 추론속도를 보장할 수 있다는 사실은 눈여겨볼만한 것 같습니다.
  • 그래프 스펙트럼 컨볼루션의 부담되는 연산량을 해결하기 위해, Shift operator인 그래프 라플라시안 행렬의 거듭제곱 항을 Sobolev term 꼴의 Hadamard product 연산으로 대체할 수 있다는 fundamental observation을 제공하고, GCN의 동일한 컨볼루션 연산을 일반화하여 단순하지만 연산 효율성이 크게 향상되고 강건한 성능을 보장할 수 있는 S2-GNNs을 제안하였습니다.
  • 논문 끝에 몇가지 한계점도 제시하고 있습니다. 파인튜닝을 요구하는 α, ϵ, 그리고 Fusion layer 구성 등의 3가지 파라미터 존재로부터 기존 GCN보다 복잡도가 여전히 높으며, 파라미터 최적화 과정의 어려움 때문에 실제 시나리오 적용에 아직 해결해야할 부분이 남아있다고 합니다.
  • 개인적으로 위 논문을 읽으면서 저자들이 새롭게 발견한 사실과 그 기반으로 간단하게 제안된 S2-GNNs의 기여는 확장성 및 효율성 문제로 실제 시나리오에서 널리 활용되지 못하고 있는 기존 그래프 스펙트럼 신경망 모델의 한계를 조금이나마 덜어준 느낌이 듭니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn

Subscribe for daily recipes. No spam, just food.