24년 11월 3주차 그래프 오마카세
Graph Classification Gaussian Processes via Hodgelet Spectral Features
paper link : https://arxiv.org/abs/2410.10546
- 최근 연구실의 세미나 발표를 듣고, 그래프 가우시안 프로세스 (graph GPs)이라는 분야에서의 다양한 연구들을 접하게 되었습니다. 저는 다음 확률적 프로세스 (Stochastic processes)에 대한 관련 지식이 넓지 않지만 해당 발표를 들으면서 흥미로운 내용들이 많이 있는 듯 하여 추천받았던 논문들을 읽어보게 되었습니다.
- 일반적으로 통용되는 가우시안 프로세스(GP)란 무한 차원의 확장된 가우시안 분포를 고려하는 확률적 프로세스로써 함수들의 분포를 모델링하는 강력한 non-parametric한 기법으로 대표적으로 Bayesian ML models의 기반이 된다고 알려져 있습니다.
- 유클리드 공간에서 정의되는 GP를 (무향)그래프와 같은 비유클리드 도메인 상으로 확장시키고자 하는 선행 연구들이 존재하고 있습니다.
- Boroviskiy et.al (2019) 의 초기 연구에서는 'Mat'ern Gaussian processes'의 stochastic partial differential equations (SPDEs)의 통계적 특성들을 활용하여 Graph diffusion & Random-walk process와 밀접한 관련성을 갖는 graph Mat'ern GP를 정의하였습니다.
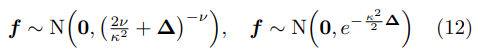
- 다음 graph Mat'ern GP의 공분산 행렬이 그래프 구조를 반영한다는 정보로부터 Graph classification 등의 Downstream tasks에서 이를 활용하는 연구들이 제안되고 있습니다. 대표적으로 Opolka et al.(2023)은 해당 공분산 행렬의 Positive semi-definite한 특성을 기반으로 Graph signal wavelet transform을 통한 Spectral node features을 학습하는 두 제안 모델 FT-GP, WT-GP의 Synthetic & Real-world Graph Classification 분야에서 우수한 성능을 보여주었습니다.
- 흥미롭게도 Opolka et al.의 Graph signal processing (GSP) 기반 아이디어를 Topological signal processing (TSP) 도메인으로 확장시킨 연구 논문을 찾을 수 있어서, 이번 주 오마카세에서 해당 논문을 전달해드리고자 합니다.
Gaussian Processes for Graph Classification
- 그래프 노드 상에서 정의된 graph GP을 Hodge-theory 기반 Simplicial complexes의 엣지 (1-complex) 상의 GP로 확장시키는 방법을 제안합니다. 한마디로, Higher-order networks (i.e. complex representation) 상의 GP를 정의하는 방법을 소개합니다.
- 핵심 아이디어는 이전 연구와 동일하게 Graph signal wavelet transform 기법을 사용하여 graph Laplacian & graph Helmhozian 행렬의 고유분해로부터 노드 및 엣지 상에 적용가능한 확장된 공분산 커널을 설계하는 방향으로 접근합니다.
- 구체적으로, Incidence matrix (Bve, Bet)를 기반으로 노드(v)와 엣지(e) 간의 관계성을 인코딩하는 0th Hodge Laplacian = graph Laplacian Lv(i):=Bve(i)Bve(i)T, 엣지와 면 간의 관계성을 인코딩하는 1th Hodge Laplacian = graph Helmhozian Le(i):=Bve(i)TBve(i)+Bet(i)Bet(i)T을 만족하는 사실로부터 접근합니다. 즉, Hodge Laplacian 행렬은 두 행렬의 일반화 형태로 이해해볼 수 있습니다.
- 그로부터 graph Laplacian & Helmhozian의 Decomposition 연산을 Hodge Decomposition으로 얻어낸 3가지 하위공간(Exact, Co-exact, Harmonic space) 상의 Spectral features을 통합할 수 있습니다.
- graph Laplacian & Helmholzian의 고유함수 (U)로부터 얻어낸 Wavelet coefficients는 식 5와 같이 정의됩니다.
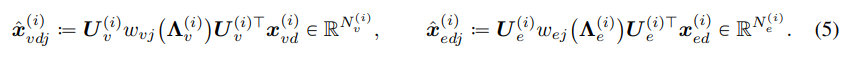
- 또한 각 행렬의 고유값 (Λ)에 적용되는 Wavelet filters는 식 3, 4와 같이 정의됩니다.
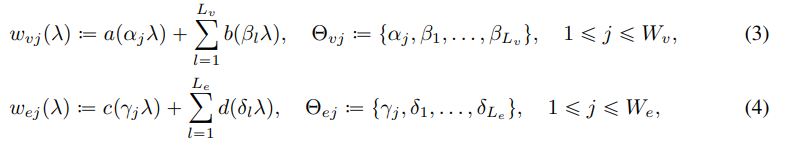
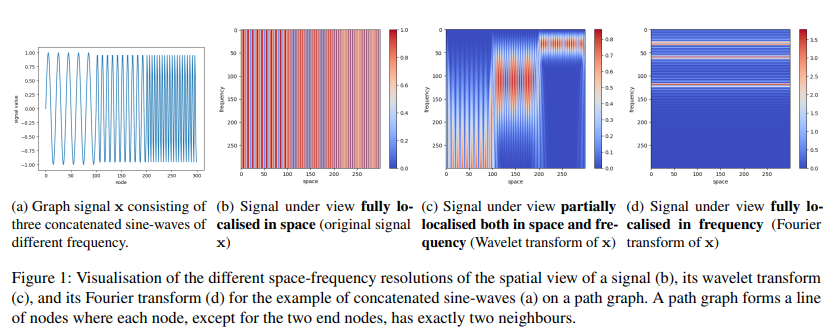
- Single scale의 Eigenfunction을 통해 수행되는 Fourier transform과 달리, 식 3의 Wavelet transform은 식 3,4와 같이 band-(b,d),low-pass(a,c) wavelet function에 scaling param (α, β, γ, δ)가 추가되어있는 형태로부터 multiple scales 상에서 다양한 resolution의 flexible spectral features를 얻어낼 수 있다는 장점을 가지고 있습니다. 아래의 Figure를 통해 시각적으로 확인해볼 수 있습니다.
💡
A wavelet filter is a combination of a scaling function at a single scale and a wavelet function at multiple scales, offering multi-scale resolution.
To compute the more flexible graph wavelet coefficients [8] (see Appendix B) by modulating Fourier coefficients using a wavelet filter on the eigenvalues Λv(i) and Λe(i).
To compute the more flexible graph wavelet coefficients [8] (see Appendix B) by modulating Fourier coefficients using a wavelet filter on the eigenvalues Λv(i) and Λe(i).
- 다음 Wavelet transform 연산을 노드 및 엣지 고유기저들(식 6)에 적용하여 Hodgelet spectral features을 얻어내게 됩니다.
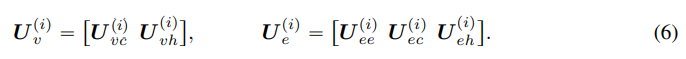
- 다음 기저들의 구성을 이해하기 위해, 각 공간 (exact, co-exact, harmonic)의 특성을 다시금 상기시켜봅시다. 엣지 공간을 중심으로 생각하고 있기 때문에 k=1로 가정합니다.
- Exact (Curl) subspace, im(B2) : 2-simplices, 면 상에서 순환하는 edge-flow 특성이 포착되는 공간입니다. 다음 공간은 고유벡터 Uee로부터 span되며 div-free하기 때문에 Uv의 영향을 받지 않습니다. 따라서 [Uv]에 포함되지 않았습니다.
- Co-exact(Div) subspace, im(B1T) : 0-simplcies, 노드의 gradient (inflow, outflow) 정보가 포착되는 공간입니다. 다음 공간은 고유벡터 Uvc 로부터 span되며 curl-free 하기 때문에 Ue의 영향을 받지 않습니다. 따라서 [Ue]에 포함되지 않았습니다.
- Harmonic subspace, ker(L1) : 모든 Simplices 상의 flows (node gradient, edge-flow) -> 0으로 수렴하여 오직 hole-flow만 포착하는 공간입니다. 해당 hole의 구성 요소인 노드, 엣지의 고유벡터 Uv,e 로부터 공통적으로 span되기 때문에 [Uv,e] 에 모두 포함되어 있습니다.
- 노드 및 엣지 고유벡터 Uv,e 의 요소별 wavelet coefficients를 계산하고 (xvc,vh, xee,ec,eh) 동일한 요소들끼리 concatenation하여 최종 Hodgelet spectral feature를 얻어냅니다. 통합하여 전체적인 Hodgelet kernel을 아래 식 7과 같이 정의합니다. 다음은 주어진 Simplicial complex의 전체적인 구조정보를 인코딩하는 graph GP의 공분산 커널을 대체하여 활용됩니다
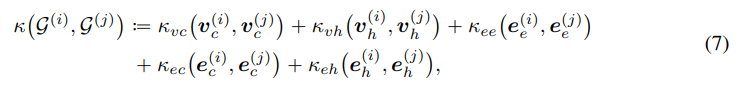
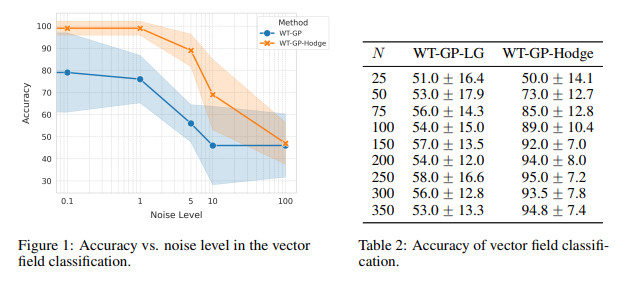
- Hodgelet kernel-based GPs는 scalability, flexibity 등의 강력한 장점들을 기반으로 거대한 크기의 수많은 데이터에 손쉽게 호환 가능하며, 한번의 Decomposition 연산만을 요구하기 때문에 선행 모델(FT-GP, WT-GP)보다 좋은 효율성을 강조할 수 있음을 언급합니다. 실험 결과를 통해 다음 사실들을 입증합니다.
💡
Separate kernel for each part of the Hodge decomposition offers greater flexibility. We highlight that our GP-based classification algorithm supports multi-dimensional spatial graph features and graphs of varying sizes, in contrast to typical graph kernel-based methods.
The GP component scales according to the number of graphs, while the eigendecompositions are a one-off cost that can be performed in advance.
The GP component scales according to the number of graphs, while the eigendecompositions are a one-off cost that can be performed in advance.
- 이번 주 오마카세에서는 GSP 기반으로 구축된 기존 그래프 상의 가우시안 프로세스(GP) 도메인을 TSP 기반의 Simplicial complex으로 확장하는 방법을 소개한 논문을 전달해드렸습니다. 주요 Contributions을 아래와 같이 3가지로 간략하게 정리해볼 수 있을 것 같습니다.
- Graph classification에서 중요한 정보인 그래프의 전체 구조 정보를 담고 있는 공분산 커널함수 설계를 기반하여 Simplicial complex로의 확장을 목표로 두고 있습니다.
- 기존 graph Laplacian & Helmhozian Wavelet function (식 3~5) 을 Hodge Laplacian으로 통합하고, Decomposition을 통해 얻어낸 Hodge subspaces의 기저 요소(식 6)들에 transformation 연산을 수행하여 최종적인 Hodgelet spectral features를 얻어내는 과정을 소개하였습니다.
- graph GPs의 공분산 커널함수를 Hodgelet kernel 함수로 대체함으로써 다양한 graph classification tasks에서 선행 연구 결과를 능가할 수 있음을 보여주었습니다. 더욱 향상된 flexibility 및 scalability 효과를 얻어낼 수 있음을 실험 결과를 통해 보여주었습니다.
- 이전과 비슷하게 Simplicial complex의 TSP 개념만 가지고도 쉽게 이해할 수 있을 정도의 깔끔한 논문이라 느껴졌습니다. 이런 흐름의 연구들을 보면 토폴로지의 기본적인 개념들만 잘 숙지해두어도 그래프 관련 다양한 문제들에 쉽게 접근하고 좋은 성능을 기대해볼 수 있을 것으로 생각합니다.
[Contact Info]
Gmail : jhbae1184@akane.waseda.jp
Twitter (X): @jhbae1184
