24년 10월 5주차 그래프 오마카세
TopoTune : A Framework For Generalized Combinatorial Complex Neural Networks
paper link : https://arxiv.org/abs/2410.06530
official link : https://github.com/geometric-intelligence/TopoBenchmark?utm_source=catalyzex.com
Index
- What is combinatorial complex ? --> N_up&down incidence, N_up&down Adjacency, Augmented Hasse Graphs, CCNN's message passing mechanism.
- Generalized Combinatorial Complex Neural Networks (GCCNs) --> Strictly augmented Hasse graphs, Per-rank neighborhoods.
- Simplicial complex, Cell complex, Cech complex, Alpha complex 등 데이터의 토폴로지 구조 및 그 특성을 표현할 수 있는 방법들은 많습니다. 하지만 정의되는 방법 차이에 따라 각 complex에서 나타나는 고유한 토폴로지 특성들은 다릅니다.
- 즉, 주어진 데이터에 적합한 토폴로지 표현 방법을 선택하고 활용하는 것은 매우 중요할 것이며 그러기 위해서 도메인의 배경 지식 등의 추가 정보들을 요구할 수도 있을 것입니다. 이는 토폴로지 데이터 분석 (TDA)의 Validation & Scalability limitation과 연결되는 부분입니다.
- 전통 머신러닝의 Hand-crafted feature extraction과 유사한 부분으로 생각됩니다. 중요한 토폴로지를 뽑아내기 위한 여러가지 요소들을 고려해야 하고 전문가 검증 등의 과정이 추가된다면 매우 시간 소모적일 수 밖에 없을 것입니다.
- 그로부터 (자연스럽게) 토폴로지 딥러닝 (TDL)이란 도메인이 생겨나게 되었고, 기존 딥러닝과 유사하게 모델이 스스로 입력 데이터에 맞는 토폴로지 구조를 학습할 수 있는 여러 알고리즘들이 제안되어져 왔습니다. 위의 Scalability 뿐만 아니라 Parameter tuning, Loss information 등 성능 향상의 여러가지 어려운 원인들을 단번에 해결할 수 있습니다. 하지만 TDL 모델은 일반 딥러닝 모델들보다 학습 파라미터 개수가 매우 많기 때문에 Computational cost 문제가 가장 우선시 해결되어야 할 문제로 고려되고 있으며, 모델 학습을 위한 필수적인 토폴로지 정보의 벡터화 (Vectorization) 과정을 위한 Lack of Universial framework 역시 해결되어야 합니다.
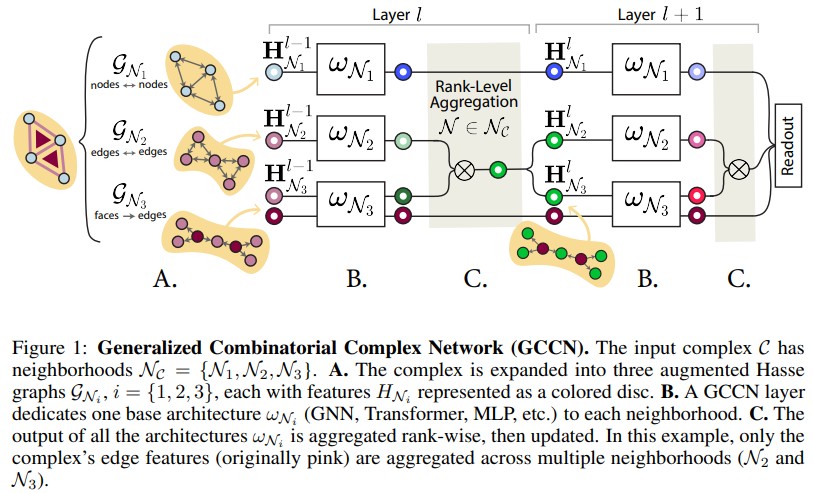
- 이번 주 오마카세에서 전달해드릴 논문은 Combinatorial Complex라는 Generalized complex 구조를 딥러닝 방식으로 처리할 수 있는 신경망 모델 CCNN을 개선한 GCCN (상단의 Fig 1 참고) 및 해당 소프트웨어 툴인 TopoTune에 대해 소개해드리고자 합니다. 한마디로 일반화된 TDL 프레임워크로 받아들여주셔도 될 것 같습니다.
What is combinatorial complex ?
- 저자들은 Combinatorial complex에 대한 개념을 Section 2. Background에서 가볍게 소개해주고 있습니다. 보다 자세한 설명은 'Topological Deep Learning: Going Beyond Graph Data' 원본 논문에서 제공하고 있습니다.

- Combinatorial complex, 줄여서 CC, 는 3가지 요소로 구성되어 있으며 노드 집합 V, 토폴로지를 정의하는 노드 멱집합의 하위집합 C, 그리고 토폴로지 차원을 정의하는 랭크 (rk)함수가 포함됩니다.
- 만족해야 하는 2가지 조건이 존재합니다.
- 모든 노드에 대하여 모든 토폴로지 구조에는 최소 1개 이상의 노드가 포함되어있어야 하며, 1개로만 구성된 토폴로지의 랭크는 0이다.
- 포함 관계 (incidence relation)를 만족하는 두 토폴로지에 대하여, Co-face의 랭크가 face의 랭크보다 크거나 같음.
- Simplicial complex의 요소 간 포함 관계를 확장하여 공간 간의 포함 관계를 정의한 것으로 이해해볼 수 있겠습니다. 즉 다음을 공간의 차원으로 바라보면 랭크가 큰 토폴로지 요소의 공간 상에 랭크가 작은 토폴로지 요소의 공간이 존재해야 합니다.
- 위의 조건을 만족하는 C의 요소들을 'cell'이라고 부르며, 가장 큰 cell 랭크 값을 해당 C의 차원으로 정의합니다. 다음은 기존 Complex 개념과 동일한 부분이기에 생략하겠습니다. (0차원 - 노드 공간, 1차원 - 엣지 공간, 2차원 - 면 공간 ..)
- 포함 관계를 기반으로 up & down incidences (I, ↑↓)를 통한 CC 상의 이웃 개념(Neighbors, N)을 아래의 식 1과 같이 정의합니다. 다음은 다른 차수 간의 이웃 관계입니다.
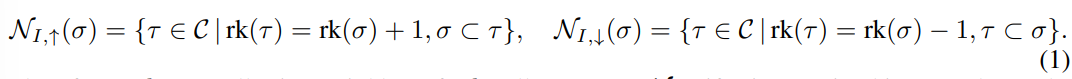
- N_up incidence (\sigma) : 토폴로지를 구성하는 요소에 대하여 1차원 낮은 공간 속의 \sigma를 포함하는 요소들의 집합 (\tau). 예를 들어 특정 노드의 N_up incidence는 그 노드를 끝점으로 갖는 엣지로 생각할 수 있습니다.
- N_down incidence(\sigma) : 토폴로지를 구성하는 요소에 대하여 1차원 높은 공간 속의 \sigma에 포함되는 요소들의 집합. 예를 들어 특정 엣지의 N_down incidence는 그 엣지의 양 끝점인 노드들로 생각할 수 있습니다.
- 또한, up & down Adjacencies (A, ↑↓)를 통한 CC 상의 이웃 개념도 아래 식 2와 같이 정의합니다. 다음은 같은 차수 간의 이웃 관계입니다.
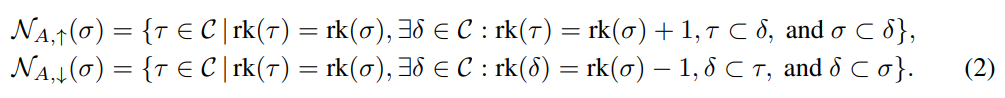
- Incidence에 추가적인 \delta 요소가 포함됩니다.
- N_up Adjacency (\sigma) : 위의 N_up Incidence 관계를 만족하는 \tau, sigma 요소들을 모두 포함하는 임의의 \delta가 C에 포함되어있을 때, \sigma와 동일한 차수를 갖는 \tau의 집합. 예를 들어, 두 노드 \tau, sigma에 대하여 그 노드들을 끝점으로 갖는 엣지 \delta가 존재할 때, 그 노드들의 관계를 의미함.
- N_down Adjacency (\sigma) : N_down Incidnece 관계를 만족하는 \tau, sigma 요소들에 포함되어 있는 임의의 \delta가 존재할 때, \sigma와 동일한 차수를 갖는 \tau의 집합 . 예를 들어, 두 엣지 \tau, sigma에 대하여 동일한 노드 \delta를 끝점으로 가지는 경우의 두 엣지의 관계를 의미함.
- 해당 개념은 설명으로 보기엔 직관적으로 받아들이기 매우 어렵습니다. 다음은 CC 상의 각 cell들을 노드로 표시하여 동일 & 다른 차수 간의 관계성을 명시적으로 나타내는 Augmented Hasse graph를 통해 쉽게 이해하실 수 있습니다. (Fig 2 참조)
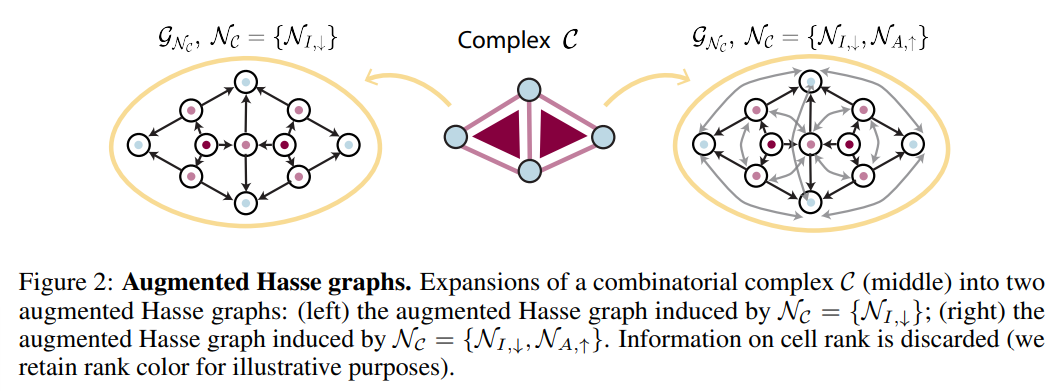

- Augmented Hasse Graph, 줄여서 AHG,는 각 CC의 cell을 노드로 정의하고 임의의 이웃 함수 (Incidence, Adjacency)에 대하여 그 정의를 만족하는 모든 노드들을 연결한 유향 그래프 구조.
- Fig 2의 좌측 AHG는 CC 상의 노드를 파랑 포인트, 엣지를 분홍 포인트, 면을 빨간 포인트로 표현하였을 때, N_down incidence을 만족하는 유향 그래프를 보여주고 있습니다.
- 우측은 동일한 CC에 대하여, N_down incidence (검정색 화살표) + N_up adjacency (회색 화살표)를 동시에 만족하는 유향 그래프를 보여주고 있습니다.
- 위의 이웃 함수 정의들을 기반으로 동작하는 Combinatorial Complex Neural Network (CCNN)의 메세지 전달 메커니즘 (식 3)은 논문의 설명으로 대체하겠습니다.
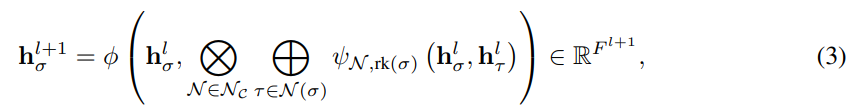
💡
The embedding of a cell is updated in a learnable fashion by first aggregating messages with neighboring cells per each neighborhood, and then by further aggregating across neighborhoods. We remark that by this definition, all CCNNs are message-passing architectures.
- XOR 기호 : N_up&down incidence의 관계성 정보를 통합하는 함수
- 텐서 곱 기호 : N_up&down adjacence의 관계성 정보를 통합하는 함수
- CCNNs의 메세지 전달은 GNNs의 메세지 전달의 고차수 관계 정보에 대한 일반화된 메커니즘으로 쉽게 대체될 수 있으며, 손쉽게 기존 그래프 라이브러리 (e.g. Torch geometric)를 통해 표현력 손실 없이 구현될 수 있음을 본 논문에서 언급합니다. 차후 CCNNs의 개선 모델인 GCCNs의 아키텍처를 구현한 TopoTune 역시 Torch-gemoetric 기반의 라이브러리를 기반으로 구현되었습니다.
- 최신 연구에 따르면, AHG 그래프 상에서 GNNs은 동일한 차수 및 다른 차수 (혹은 랭크)의 cell들 사이의 관계성을 한번에 통합할 수 없기 때문에 현 CCNNs의 메커니즘을 대체할 수 없음이 밝혀졌습니다. 다음은 해당 논문의 실험 파트에서 4가지 base GNNs (GCN, GAT, GIN, SAGE)의 정성적 결과를 통해 확인해볼 수 있습니다.
GENERALIZED COMBINATORIAL COMPLEX NEURAL NETWORKS (GCCNs)
- CCNNs의 개선을 위한 메세지 전달 메커니즘을 확장시켜 일반화시킨 모델 GCCNs은 2가지 새로운 표현을 사용합니다.
Ensemble of Strictly augmented Hasse graphs
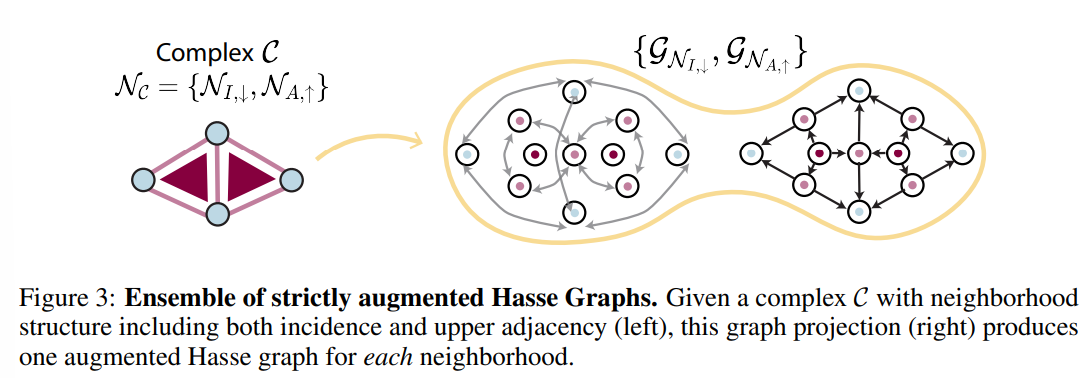
- Fig 3에서와 같이, Fig 2의 AHG를 이웃 관계에 따른 (엄격하게 분리된) N_incidence based Hasse Graph 및 N_adjacency based Hasse Graph의 메세지 전달 메커니즘을 앙상블하는 방법으로 구현하였습니다. 그로부터 식 4의 AHG 정의를 아래의 식 5와 같이 수정합니다.
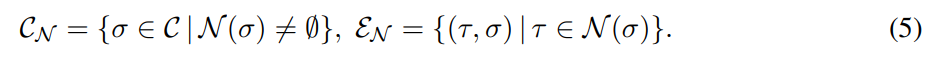
- 그럴싸한 아이디어에 비해 매우 간단합니다. 임의의 이웃 함수 (N_incidence & adjacency) 정의에 따라 반드시 이웃이 정의되는 Cell에 대하여 그 이웃과 연결되는 요소들만을 Hesse graph로 표현합니다. 그리고 이들을 하나의 AHG로 projection하여 |N_C|개의 확장 그래프를 얻어낼 수 있습니다.
Per-rank Neighborhoods
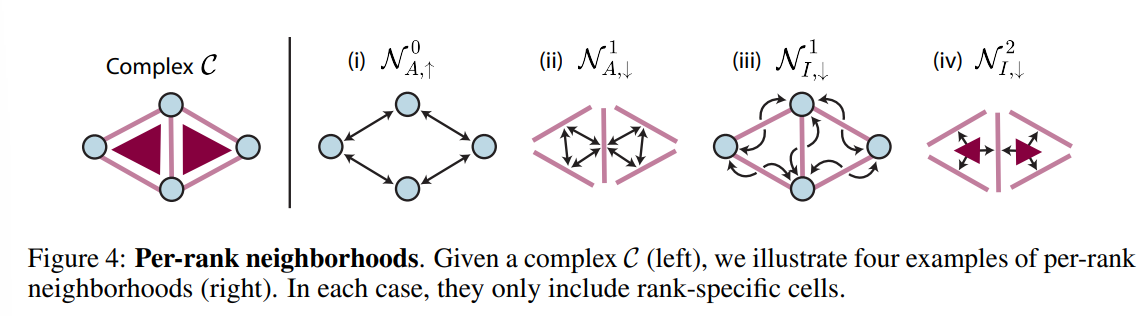
- 앞서 소개해드린 이웃 함수들의 강한 제약조건을 완화하기 위한 새로운 이웃 함수, Per-rank Neighborhoods, 를 도입하였습니다.
- Fig 2의 우측 그래프 (N_down incidence + N_up adjacency)를 예시로 살펴봅니다. N_down incidence에 대하여 노드(N)-엣지(E) & 엣지(E)-면(T) 사이의 메세지 전달 과정이 이루어집니다.
- 여기에서 동일한 엣지 E에 대하여 E와 N_down incidence인 끝점 노드 N들과 메세지 전달이 이루어질 때 E를 N_down incidence로 갖는 면 T와의 메세지 전달은 이루어질 수 없습니다.
- N_up adjacency에 대하여 노드(N)-노드(N) & 엣지(E) - 엣지(E) 사이의 메세지 전달이 이루어집니다.
- 마찬가지로 두 노드가 서로 메세지 전달을 수행할 때, 그 노드들을 연결하는 엣지에서는 메세지 전달이 이루어질 수 없습니다.
- 즉, 식 1,2으로 정의된 이웃 함수들 상에서는 병렬적으로 메세지 전달 메커니즘을 수행할 수 없습니다. 그로부터 연산량이 폭발적으로 늘어나게 됩니다.
- Fig 2의 우측 그래프 (N_down incidence + N_up adjacency)를 예시로 살펴봅니다. N_down incidence에 대하여 노드(N)-엣지(E) & 엣지(E)-면(T) 사이의 메세지 전달 과정이 이루어집니다.
- 다음을 해결하기 위해 제안된 Per-rank neighborhoods 함수는 이웃 함수의 제약적 정의를 따라가되, 특정 차원 (혹은 랭크)의 cell만 고려하기로 하고 그 외의 다른 차원의 cell은 모두 0으로 맵핑시킵니다. 역시 매우 단순한 아이디어입니다.
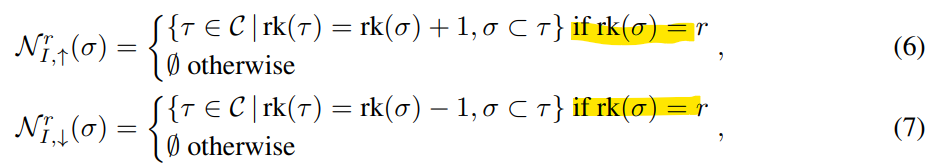
- Fig 4와 같이, (i) N_up adjacency을 만족하는 0차 cell (노드)만을 고려하여 그들 사이의 메세지 전달만을 수행하고 그 외의 조건을 만족하지 않는 모든 cell들은 없애버렸습니다. 그로부터, 노드-엣지 상의 메커니즘으로만 학습이 집중됩니다.
- (iii) N_down incidence를 만족하는 1차 cell(엣지)와 0차 cell (노드)만을 남겨 이들 사이의 메세지 전달만을 수행하고 그 외의 조건을 만족하지 않는 모든 cell들은 없애버렸습니다. 그로부터 노드-노드 상의 메커니즘으로만 학습이 집중됩니다.
- AHG 상에서의 Per-rank neighborhoods 함수는 정보 손실 등의 큰 문제가 있을 것 같습니다. 하지만 이전에서 정의된 Strictly AHG 상에서 얻어낸 |N_C| 개의 그래프 상에 개별적으로 Per-rank neighborhoods 함수를 적용하여 메세지 전달을 수행하고, 이들을 앙상블하여 업데이트 결과를 얻어내었을 때 더욱 개선된 성능을 얻어내었다고 합니다.
- Ensemble of strictly AHG + Per-rank neighborhoods의 과정을 모두 포함하여 기존 CCNNs을 개선한 모델을 GCCNs으로 명칭하였습니다. 다음 과정을 식 8로써 아래와 같이 정의합니다.
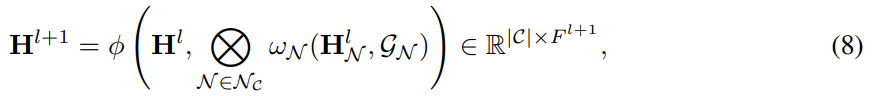
- 입력된 strictly AHG 그래프에 대하여, w_N은 학습 가능한 메세지 전달 함수로 기존 신경망 모델을 활용할 수 있습니다. (GNN, Transformer ..) 그리고 텐서 곱 연산을 통해 Per-rank Neighborhoods 함수의 조건을 만족하는 cell들의 메세지들을 집계하고, 학습 가능한 업데이트 함수 (\phi)를 통해 다음 레이어로 넘어가는 구조입니다.
- Per-rank neighborhood의 조건으로부터 선택된 이웃 함수 (incidence, adjacency) 정의를 만족하는 cell들만 고려하게 되었으므로 식 3의 기존 CCNNs의 메세지 전달 공식보다 훨씬 단순화되면서 큰 연산적인 효과를 얻어올 수 있습니다.

- 위의 설명들을 기반으로 GCCNs의 아키텍처 (Fig 1)을 쉽게 이해해볼 수 있겠습니다. 그래프 분류 문제의 경우, 최종 레이어 이후 Readout 레이어를 추가하여 전체 그래프 정보를 종합합니다.
- GCCNs은 CCNNs의 일반화된 아키텍쳐로써 기존 CCNNs의 특성들을 유지하고 있다는 사실을 Appendix A에서 보입니다.

- 실험 파트에서 다양한 노드 및 그래프 분류 문제 (e.g. molecules, proteins)에 대한 폭넓은 실험 결과들을 제공함으로써 제안 GCCNs이 CCNNs보다 향상된 성능과 더 작은 크기로써 효과적으로 일반화할 수 있음을 보여줍니다.
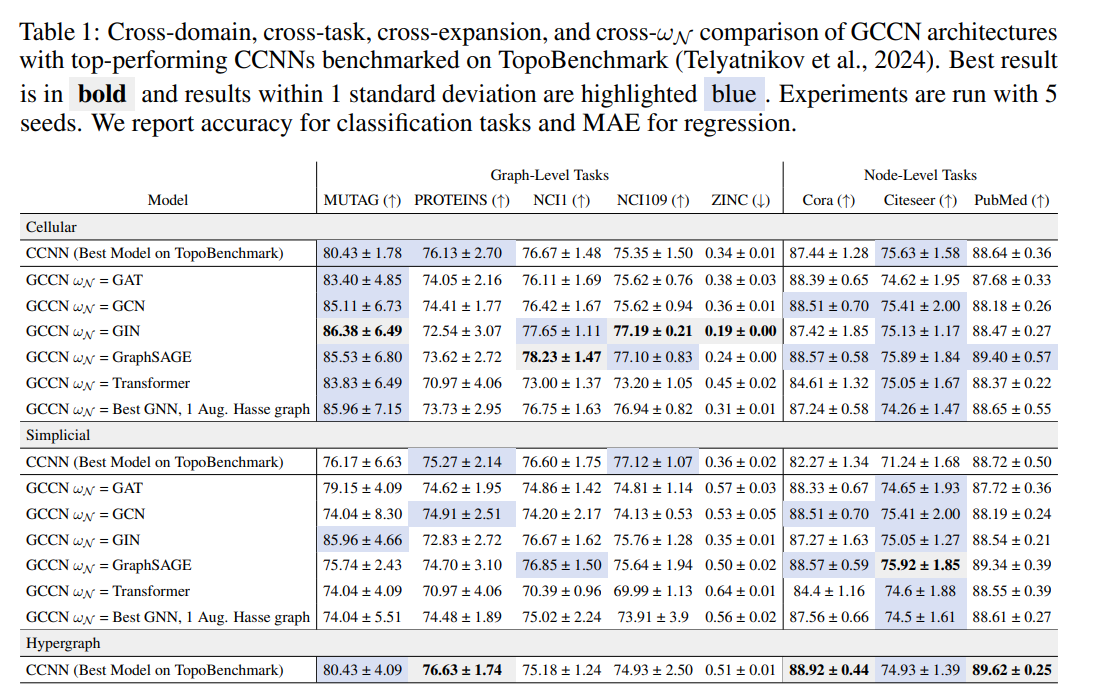
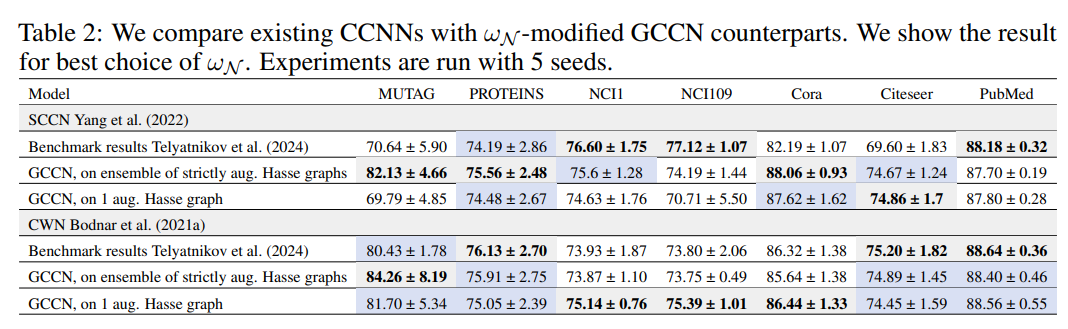
- 이번 주 오마카세는 앞서 많이 다루었던 TDA 방법들을 딥러닝 방법으로 해결하는 TDL 분야의 일반화된 모델, GCCNs을 제안한 논문을 소개해드렸습니다. 기존 CCNNs의 일반화된 모델이 제안되었었으나, 메세지 전달 과정에 있어서 존재하는 강한 제약조건으로부터 발생되는 연산량 문제를 해결하고 다양한 태스크의 문제에서 성능을 개선하는 Advanced generalized TDL model로써 생각해볼 수 있을 것 같습니다.
- 2가지 핵심 아이디어로 Ensemble of strictly Augemented Hasse Graph 및 Per-rank Neighborhoods를 본 논문에서 설명해주었습니다. 뜯어보니 상당히 간단한 아이디어임에도 좋은 효과를 보여준 것에 선택의 이유로써 고려했던 것 같습니다.
- 그리고 Combinatorial Complex라는 개념의 이해와 CCNNs의 동작 메커니즘을 이해하는 부분도 가볍게 이해하는 것만으로 충분히 해당 논문의 설명 흐름을 받아들이는 데 어려움은 없을 것으로 생각합니다.
- 이것들의 자세한 이해를 위한 충분한 시간적 투자가 필요할 것 같습니다. 오마카세에서는 필자의 이해력 부족으로 인해 좀 가볍게 다루고자 이러한 것들을 생략하였으나, 관심이 많으신 독자분들께서는 제가 링크로 걸어둔 논문들을 참고하시면 큰 도움이 되실거라 생각합니다.
[Contact Info]
Gmail : jhbae1184@akane.waseda.jp
Twitter (X): @jhbae1184
