25년 4월 2주차 그래프 오마카세
On Vanishing Gradients, Over-Smoothing, and Over-Squashing in GNNs: Bridging Recurrent and Graph Learning
paper link : https://arxiv.org/abs/2502.10818
- 오마카세에서 여러번 다루었던 주제로, 그래프 신경망의 대표 학습 메커니즘인 메세지 전달 방법의 한계점을 심층적으로 분석하는 논문을 가볍게 리뷰해보고 해당 논문에서 강조하는 핵심 인사이트를 전달해드리고자 합니다. 좋은 참고가 되었으면 좋겠습니다.
- 다들 잘 아시고 계시는 문제점인 Over-smoothing, Over-squashing의 문제점들을 Vanishing gradient의 관점에서 재조명하고, 통합적으로 분석하여 다루고 있습니다. 그리고 다음 문제점들을 Linear control theory 관점에서 Recurrent model과 State-stae model을 활용하여 해결하고자 한 점이 기여도로써 인정받고 있습니다.
- 특히 Vanishing gradient가 GNN의 표현력 감소에 미치는 영향과, Recurrent 모델에서 사용되는 기술들이 위 문제 해결에 어떻게 도움이 될 수 있는지를 깊게 탐구하여 독자들에게 제공하고 있어, 이 부분에 집중하여보면 좋을 것 같습니다.
💡
(본 논문에서 발췌)
Message of the Section: GNNs, especially GCNs and GATs, experience a phenomenon we term “extreme gradient vanishing” due to the use of a normalized adjacency for the message passing operation. Reinter- preting any GNN as a recurrent model enables direct control of the Jacobian spectrum, which mitigates this issue while preserving architectural generality.
Message of the Section: GNNs, especially GCNs and GATs, experience a phenomenon we term “extreme gradient vanishing” due to the use of a normalized adjacency for the message passing operation. Reinter- preting any GNN as a recurrent model enables direct control of the Jacobian spectrum, which mitigates this issue while preserving architectural generality.
- 핵심 내용을 요약하면 아래와 같습니다.
- GNN을 recurrent model로 재해석: GNN의 message passing 과정을 recurrent neural network (RNN)의 hidden state 업데이트 과정과 유사하게 해석합니다. 이를 통해 gradient 소실 문제에 대한 새로운 시각을 제시합니다.
- GNN의 layer-wise 업데이트 과정을 State-space 모델로 표현하고, RNN과의 유사성을 강조합니다. 해당 논문의 식 9에 정의되어 있으며, 기존 GNN은 상태 변환 행렬(Λ)이 갖는 Memory 역할이 없는 일반적인 인접 행렬 (A)의 memoryless 방식으로 동작하는 것의 문제점을 강조합니다.
- GNN-SSM (State-Space Model) 제안: Jacobian (다변수 함수의 1차 편미분 값을 행렬꼴로 나타낸 것)의 spectrum(행렬의 eigenvalue 집합)을 조절하여 Vanishing gradient 문제를 완화할 수 있는 state-space 모델 기반의 GNN 구조를 제안합니다.
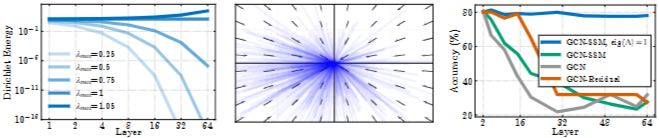
- 여기에서는 Jacobian을 이용한 Gradient Propagation을 분석합니다. 구체적으로 GCN layer의 Jacobian singular value spectrum이 Normalized Adj matrix의 spectrum에 의해 조절됨을 수학적으로 증명합니다. Fig 2에 경험적인 증명 결과를 제시하고 있습니다.
- 그로부터 GNN-SSM이라는 새로운 State-space 기반 GNN 구조를 제안합니다. 다음 모델은 Jacobian의 spectrum을 상태 변환 행렬(Λ)의 고유값에 의해 직접 조절될 수 있도록 합니다. 해당 고유값을 1로 설정하여 Jacobian을 Edge of Chaos(gradient가 폭발하거나 소실되지 않고 안정적으로 유지되는 상태. GNN 학습에 최적의 상태입니다.)로 만들어 문제를 완화시킵니다. (Fig 3 참고)
- Vanishing gradient과 Over-smoothing의 연관성 규명: layer-wise Jacobian의 spectrum 분석을 통해 Vanishing gradient이 Over-smoothing의 주요 원인임을 밝힙니다. Jacobian의 contraction으로 인해 노드 특징(node feature)이 0으로 수렴하면서 Dirichlet energy(그래프 신호의 smoothness를 측정하는 지표)가 최소화되는 현상을 설명합니다.
- 세션 4의 내용을 읽어보면, (Lemma 4.1) ReLu 혹은 Tanh와 같은 활성화 함수를 사용하는 GNN layer에서 0벡터에서 특징 벡터들이 모두 0으로 수렴하게 됩니다. 그로부터 (Proposition 4.2) GNN의 repeated application은 노드 feature를 0으로 수렴시킨다는 사실 및 (Proposition 4.3) Dirichlet energy가 Jacobian의 contraction에 의해 빠르게 감소되는 사실을 보입니다.
- 즉, GNN 레이어의 반복 적용은 입력 벡터의 Norm 및 Smoothness르 감소시켜 모든 노드의 특징이 0으로 수렴하게 만드는 사실을 강조합니다. 이는 Vanishing Gradients 문제와 연결되기에 전체적인 모델의 표현 학습 능력을 저하시킬 수 있습니다.
- GNN을 recurrent model로 재해석: GNN의 message passing 과정을 recurrent neural network (RNN)의 hidden state 업데이트 과정과 유사하게 해석합니다. 이를 통해 gradient 소실 문제에 대한 새로운 시각을 제시합니다.
💡
(본 논문에서 발췌)
Message of the Section: There exists a direct link be- tween the over-smoothing phenomenon in GNNs and the appearance of vanishing gradients. In particular, for contractive layerwise Jacobians and certain nonlinearities, node features collapse to a zero fixed point and thus minimize the Dirichlet energy. Hence, analyzing the spectrum of the layer-wise Jacobians will reveal if a GNN will over-smooth or not. Furthermore, borrowing techniques from RNNs to design new GNNs is expected to be an effective strategy to prevent over-smoothing.
Message of the Section: There exists a direct link be- tween the over-smoothing phenomenon in GNNs and the appearance of vanishing gradients. In particular, for contractive layerwise Jacobians and certain nonlinearities, node features collapse to a zero fixed point and thus minimize the Dirichlet energy. Hence, analyzing the spectrum of the layer-wise Jacobians will reveal if a GNN will over-smooth or not. Furthermore, borrowing techniques from RNNs to design new GNNs is expected to be an effective strategy to prevent over-smoothing.
- Vanishing Gradient와 Over-squashing 간의 연관성 분석 : Over-squashing 완화를 위해 그래프 연결성 (connectivity)을 높혀서 노드들 간의 정보 전파를 원활하게 하고 정보의 소멸현상을 방지하는 방법(Graph-rewiring)을 결합하는 것의 중요성을 강조합니다.
- 저자들은 Connectivity와 vanishing gradient 완화 기법을 결합했을 때의 결과를 실험적으로 검증하고, 이러한 접근 방식이 Sota 수준의 결과를 나타내는지 확인하고자 합니다. 이를 위해 높은 Connectivity와 'Non-Dissipativity(비소멸성)'을 결합한 최소한의 모델을 구축합니다. 여기서 'Non-Dissipativity'이란, vanishing gradients 문제가 완화되어 정보가 소실되지 않고 잘 전달되는 특성을 의미합니다.
- 해당 모델은 GNN-SSM을 통해 Vanishing gradient 문제를 완화하면서 K-hop aggregation을 통해 노드 연결성을 강화하는 kGNN-SSM 모델을 새롭게 제안합니다. 노드 분류문제에서 다음 모델의 성능을 검증하였습니다.
💡
(본 논문에서 발췌)
Message of the Section: Oversquashing in GNNs arises from both graph connectivity and the model’s capacity to avoid vanishing gradients. While most studies focus on connectivity, we argue that preserving signal strength through non-dissipative model dynamics is equally important. High connectivity allows nodes of interest to be reached in fewer message-passing steps while model dynamics ensure information is preserved.
Message of the Section: Oversquashing in GNNs arises from both graph connectivity and the model’s capacity to avoid vanishing gradients. While most studies focus on connectivity, we argue that preserving signal strength through non-dissipative model dynamics is equally important. High connectivity allows nodes of interest to be reached in fewer message-passing steps while model dynamics ensure information is preserved.
- 해당 내용의 전체 내용은 'Impact Statement' 부분에서 저자들의 요약 내용을 통해 쉽게 이해해볼 수 있을 것 같습니다. 참고하여 논문의 전체 내용을 깔끔하게 정리해보시면 좋을 것 같습니다.
[Contact Info]
Gmail: jhbae1184@akane.waseda.jp
Twitter (X): @jhbae1184