Sign in Subscribe
GraphOmakase

25년 4월 3주차 그래프 오마카세

Graphcode : Learning from multiparameter persistent homology using graph neural networks

paper link : https://arxiv.org/abs/2405.14302

  • 지속성 호몰로지(Persistent Homology)라는 개념과 그래프 이론과의 밀접한 관련에 정말 관심이 많습니다. "어떻게 데이터 구조의 지속성 (persistence) 특징을 그래프로 표현하여 신경망 학습을 효율적으로 디자인할 수 있을까?" 가 저의 최근 관심많은 연구주제이다보니 관련한 훌륭하고 재밌는 논문들을 찾아 읽어보고 있습니다.
  • 최근 위와 관련하여 정말 재밌는 논문을 하나 읽게 되어, 독자 여러분들께도 소개해드리고자 오마카세 내용으로 선정해보게 되었습니다. 많은 참고와 좋은 인사이트가 되었으면 좋겠습니다.
  • 지속성 호몰로지란, 가볍게 다시 설명드리면, 데이터의 위상적 (토폴로지) 특징을 다중 스케일로 나누어 그 변화를 추적하고 지속성의 크기에 따라 중요 특징을 뽑아낼 수 있는 토폴로지 데이터 분석 (Topological data analysis, TDA)의 핵심 개념입니다. 다음 개념은 필트레이션 (Filtration)이라는 멋진 도구를 활용하여 구현될 수 있습니다.
  • 최근 다음 정보를 머신러닝, 딥러닝에 적용해보고자 하는 연구 사례들이 증가하고 있으며, 특히 그래프 구조로 표현되는 데 적합한 호몰로지 개념을 그래프 신경망에 활용할 수 있는 이산 벡터화 (Discretizaed vectorization) 또는 적합한 그래프 표현(Graph representation)에 대한 연구가 활발히 진행되고 있습니다.
  • 해당 논문은 후자에 해당하는 것으로써, 포함 관계 (induce relation)를 활용한 필트레이션의 두가지 방향성 (Bifiltration)을 기반한 그래프 표현 방법을 제안합니다.
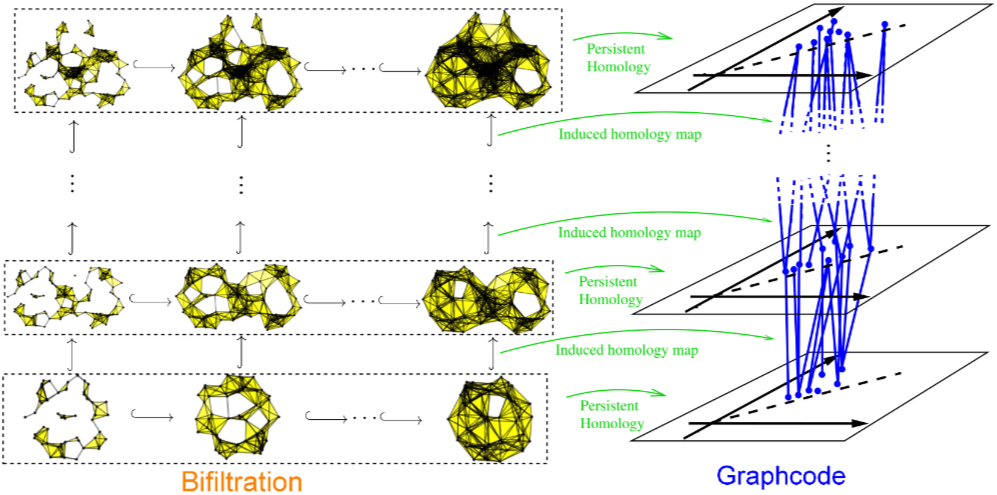
    • 위의 Figure는 Induced homology map 및 Persistent Homology의 두가지 매개변수를 기반으로 정의된 Bifiltration 상에서 데이터의 필터링 상태를 시각화하여 보여주고 있습니다. 다음 필트레이션 과정에서 발견되는 위상적 특징 (e.g. 연결요소, 구멍, 공허 등)들을 추출하고 해당 정보를 Persistent diagram이라는 2D 플롯에 (b,d) 좌표로 기록합니다.
      • b - birth : 해당 필트레이션 과정에서 데이터의 위상적 특징이 나타난 시점
      • d - death : 데이터의 위상적 특징이 사라진 시점
    • 그리고 인접한 Persistent diagram 사이의 관계를 Bipartite graph로 표현하여, 하나의 diagram 특징이 다음 diagram에서 어떻게 변화하는 지를 그래프 구조로써 인코딩합니다. 이러한 bipartite graph를 모두 합쳐서 디자인 된 새로운 데이터 구조를 Graphcode라고 명칭합니다.
  • 배경내용의 복잡성으로 인해, 자세한 설명은 생략하겠습니다. Graphcode 구성의 핵심 개념은 Barcode basis이며, 다음 basis는 Simplicial complex라는 higher-ordered한 그래프 표현의 Boundary 연산자 (하위 차원공간으로 맵핑하는 함수)를 기반으로 정의됩니다.
    • 정확하게, 다음 Boundary의 Kernel 공간의 기저를 Barcode basis라고 정의하며, 각 basis 원소는 위의 b, d 정보를 가지고 있습니다. 즉, Simplicial complex 구조 변화의 지속성을 인코딩하는 기저 벡터로 이해할 수 있습니다. 위 Figure에서 수평방향, " ->" 로 표시된 내용을 설명합니다.
    • 필트레이션 상 Boudary 연산자의 Kernel 공간의 포함 구조 (위 Figure에서 수직 방향, "↑"로 표시)를 인코딩하는 맵핑 함수도 고려하여, 해당 함수를 기반으로 bipartite graph를 표현한 것이 Graphcode로 이해해볼 수 있겠습니다.
  • 추상적인 설명은 이렇지만, 다음을 구현하기 위해서 저자들은 Boundary 연산자 행렬의 Matrix reduction 알고리즘을 적용하고 수평 방향의 필트레이션 값을 (오름차순) 정렬한 후, 수직 방향의 필트레이션 값 (오름차순) 순서에 맞추어 Boundary 행렬을 업데이트 하여 그래프를 구성합니다.
    • 여기에서 그래프 엣지는 수직 방향에서 인접한 두 Barcode bases의 변화를 추적하여 지속되는 경우에만 추가되어집니다.
  • 다음 Graphcode를 GNNs에 적용하기 위해, Graphcode에 담겨 있는 (b, d) 정보를 그래프 노드 특징으로 부여하고, Graph Attention layer 및 Local Max-pooling을 사용하여 다음 특징을 추출한 후, FFN을 통해 최종 분류 결과를 출력합니다. 다양한 그래프 분류 데이터셋 (TUdataset)에서의 실험을 통해, 기존 TDA 방법보다 높은 성능을 얻어내었으며 TDA의 특성인 Interpretibility 및 ML 통합의 적용 가능성을 보여주어 그 기여도를 인정받게 되었습니다.
  • 위상적 특징 개념에 대한 자세한 설명 및 실험 내용 등은 Appendix 부분을 참고해주시면 좋을 것 같습니다.

Algebraic Geometry Approach to Viewing Graph Solvability

paper link : https://arxiv.org/abs/2504.03637

  • SLAM(Simultaneous Localization And Mapping)에서도 그래프가 많이 활용되고 있는 것, 다들 잘 알고 계셨나요? 일반적인 그래프와 밀접한 관련이 있는 분야는 아니지만 가장 기초가 되는 정보인 카메라의 위치와 카메라 간 에피폴라 기하 (Epipolar geometry) 관계를 Viewing graph라는 새로운 수학적인 구조로 나타내어 SfM (Structure-from-Motion) 문제 (여러 이미지로부터 3차원 장면을 복원하는 문제)를 해결하는 방법론으로 활용되고 있습니다.
    • 해당 논문은 이름 그대로, SfM에서 중요한 개념인 viewing graph solvability에 대한 대수 기학적인 접근 방식을 제안하고 있습니다. 여기에서 Solvability라는 의미는 Viewing graph에 의해 주어진 카메라가 유일하게 결정되어지는 조건을 구하는 것으로 해석할 수 있습니다.
Figure 1 . Viewing graph 모식도
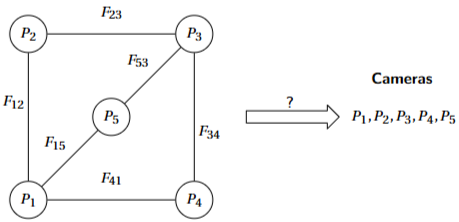
  • 위의 Figure와 같이 Viewing graph는 카메라의 위치와 관계를 그래프 형태로 표현한 것입니다. 여기에서 노드는 카메라의 위치를, 엣지는 카메라 간의 기하학적 관계 (에피폴라 기하관계)를 의미하고 있으며, Fundamantal matrix (F)으로서 인코딩됩니다. 해당 행렬은 두 카메라 간의 대응점 (corresponding points)을 연결하는 제약 조건을 담고 있습니다.
  • 위 그래프로부터 해결할 문제는 Solvability로, 주어진 viewing graph의 구조와 fundamental matrix 정보를 활용하여 카메라의 위치를 유일하게 결정할 수 있는지의 여부를 결정하는 것입니다. (화살표 ?로 표시됨.)
    • 즉, 엣지가 주어졌을 때, 그 카메라의 위치가 단 하나의 config로 결정되는지를 판단하는 것이 주요 문제라고 생각하면 될 것 같습니다.
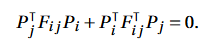
  • 다음 문제를 식 7의 방정식을 활용하여 새롭게 정의합니다. 다음 방정식은 두 카메라의 행렬 Pi와 Pj가 주어졌을 때 이를 결정짓는 유일한 Fundamental matrix (Fij)가 존재하며, 모든 엣지에 대해 다음 방정식을 수집하여 다항식 시스템을 구성합니다.
  • 해당 시스템의 Finite Solvability 판별을 위해 얻어진 다항식의 Jacobian Rank (독립적인 고유벡터 개수)를 계산합니다. Theorem 1에 설명이 나와있으며, 다음 접근법은 대수 기하학의 Fiber Dimension Theorem에 기반하여 보장될 수 있음을 설명합니다.
    • 즉, Jacobican 행렬의 Rank가 11|V| - 15 (|V| : 노드 개수)와 같다면 해당 Viewing graph는 Finite Solvability를 갖음을 증명합니다.
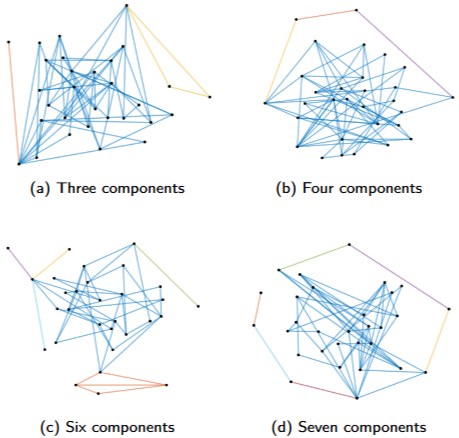
  • 위의 조건을 만족하지 않는 경우, 해당 Viewing graph를 Maximal Subgraph로 분할하는 새로운 알고리즘을 제안 및 계산하여 Finite Solvability를 만족시키도록 설계하였습니다. 다음 알고리즘의 핵심은 Jacobian 행렬의 Null space를 활용하여 각 엣지가 정확하게 한 요소에 속하게 만들어주는 것입니다.
    • 이전 관련연구에 따르면 (Proposition from 'Viewing Graph Solvability in Practice', ICCV 2023), 해당 그래프의 최대 컴포넌트 (Maximal Components - Finite Solvability를 만족하는 최대 크기의 subgraph)를 활용하면 그래프 엣지를 분할하여 unsolvable한 구조 상 solvable한 부분 구조를 분석하고 식별할 수 있음을 설명하고 있습니다.
    • 각 노드는 그래프 구조 및 연결성에 따라 여러 요소들 속에 속할 수 있기 때문에 제안 알고리즘은 하위 그래프를 순환하면서 이전에 연결된 모든 노드에 대한 Null space를 찾아 반복적으로 제약을 걸어줍니다.
  • 상당히 디테일한 수학적 증명을 기반으로 저자들의 아이디어를 탄탄하게 뒷받침 하고 있습니다. 내용이 다소 어려울 수 있으나, 주요 기여점을 우선하여 제안 방법의 키워드 내용을 잘 잡아보시는 것 만으로도 충분한 가치가 있다고 생각합니다.
    • 해당 분야에 종사하시는 연구자 및 관련 독자 여러분들께 그래프 기반의 색다른 인사이트를 드릴 수 있을 것으로 기대합니다. 관심 있으신 독자 여러분들은 시간을 투자하여 해당 논문을 찬찬히 읽어보시는 것을 추천드립니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn

Subscribe for daily recipes. No spam, just food.