25년 8월 1주차 그래프 오마카세

A General Graph Spectral Wavelet Convolution via Chebyshev Order Decomposition

paper link : https://arxiv.org/abs/2405.13806

official code : https://github.com/liun-online/WaveGC

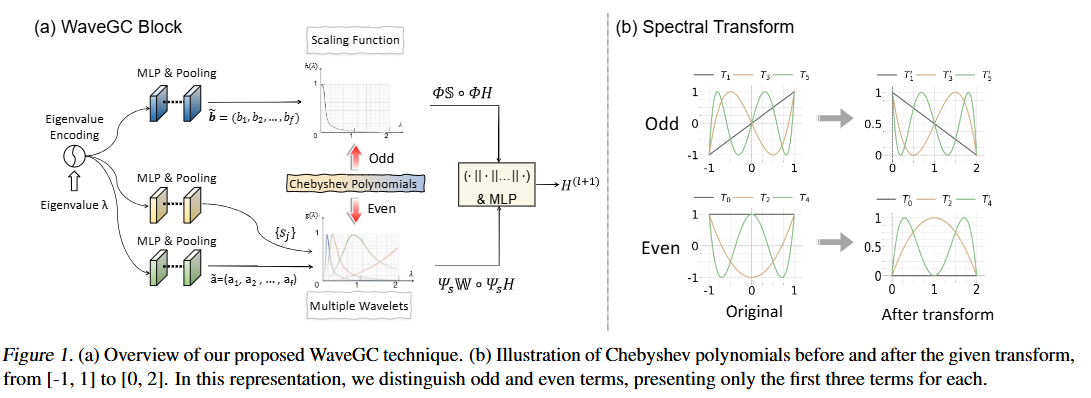
• 그래프 스펙트럼 컨볼루션은 그래프 신호처리 이론을 기반으로 그래프 필터링, 데이터 분석 등의 넓은 분야에서 활용되고 있습니다. 다음은 그래프 스펙트럼 변환을 위한 신호 기저 (고유벡터) 선택 및 주파수 계산에 설계된 파라메트릭한 커널에 의존합니다.
• 푸리에 변환 및 벡터 스펙트럼 함수에 중점을 두고 있는 기존의 기법들은 넓은 범위에 걸친 신호 분포 모델링이 필요한 작업에 제한적인 함수 용량으로 한계점을 드러내고 있습니다. 다음 문제를 해결하기 위한 새로운 그래프 웨이블릿 기반 WaveGC 라는 그래프 컨볼루션 신경망을 제안합니다.
  • Multi-resolution spectral bases & Matrix-valued filter kernel을 통합하여 이론적으로 단&장거리 신호정보를 효과적으로 포착하고 기존 방법보다 더 높은 유연성을 제공함을 입증합니다.
  • 구현에 있어서, 체비쇼프 다항식의 홀수, 짝수 항을 분리하여 일반 그래프 웨이블릿을 학습하는 새로운 기법을 도입하였습니다. 다음은 웨이블릿 허용 가능 기준(Wavelet admissibility criteria)를 엄격하게 만족할 수 있으며, 수치적인 결과에서도 일관된 성능 향상을 보임으로써 다양한 시나리오에서의 적용 가능성을 보입니다.

• 그래프 스펙트럼 웨이블릿 변환 (Spectral Graph Wavelet Transform, SGWT)은 Scalable (s_j)한 그래프 라플라시안의 고유분해를 통해 정의되며, 식 1로 나타난 특정 웨이블릿 허용 기준을 반드시 만족해야 합니다. 기준 만족을 위한 핵심 두 가지 전제 조건은 다음과 같습니다.
  • 웨이블릿은 변화하는 고주파 성분을 추출하는데 중점을 두고 있기 때문에, 0 주파수의 직류 신호(기대값 또는 저주파 정보)를 필터링하지 않습니다. 본 논문에서는 다음을 보완하기 위해 스케일링 함수 기저(h : R⁺ —> R⁺)가 별도로 존재함을 언급합니다.
• 또한 매우 높은 주파수에서는 웨이블릿 응답이 0으로 수렴해야 합니다. 즉, 무한한 주파수의 에너지를 갖지 않고, 유한한 특정 주파수 범위 내 의미 있는 정보를 추출하는 사실을 보장합니다.
• 제안 방법론의 핵심은 Multi-resolution한 adaptiveness 및 Spatial localize한 특성을 갖는 웨이블릿 기저의 학습 가능성에 있습니다. 따라서 다양한 Receptive fields를 통해 유연하게 단거리 및 장거리 신호정보를 융합할 수 있도록 학습 가능한 커널을 설계하는 것에 초점을 맞춥니다.
  • 고려해야 하는 사항은 총 세가지로, 스케일링 함수 h, 웨이블릿 기저 g, 그리고 스케일 s_j의 형태를 결정해야 합니다. 여기에서 g는 웨이블릿 허용 기준을 엄격히 만족해야 하며, h는 직류 신호를 보완하는 역할을 수행해야 합니다.
    • 이를 모두 다루기 위해, 식 4와 같이 체비셰프 다항식 (T_k)을 변환하여 활용합니다. 변환의 목적은 웨이블릿 허용 기준을 충족하고 이론적으로 유연한 g, h 함수들로 근사하기 위함입니다. Fig. 1b에 시각적인 결과도 같이 제공하여 이해를 돕고 있습니다.

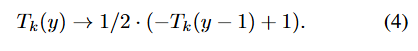
• 또한, 체비셰프 다항식의 홀수 항(T^o)과 짝수 항(T^e)을 분리하여 각각 h 및 g 함수 근사에 활용합니다. 체비셰프의 짝수 항을 통해 근사된 g 함수는 허용 기준의 첫 번째 전제조건을 만족하여 대역 통과 필터 (band-pass filter) 역할을 수행하고, 마찬가지로 홀수 항을 통해 근사된 h 함수는 두 번째 전제조건을 만족하여 직류신호를 보완하는 스케일링 함수 역할을 수행합니다. 식 5의 학습 파라미터 계수를 추가한 근사된 g, h 함수의 형태를 확인할 수 있습니다.

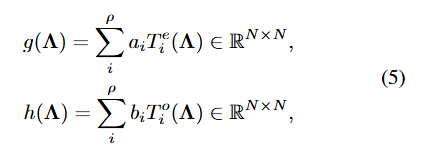
• 학습 가능한 커널을 설계하는데 저자들은 고유값 행렬의 대각요소들을 벡터로 활용하는 기존 방법을 따르지 않고, 가중치 공유를 통한 행렬 값 활용하는 더욱 효율적인 방법을 채택하였습니다. 즉, 그래프 스펙트럼 컨볼루션의 전역 주파수 패턴 포착에 일반적인 특성을 살리면서, 노드 레벨의 지역화된 주파수 패턴까지 인코딩할 수 있게 확장하여 장&단거리 신호를 포착할 수 있게 합니다.
  • 모델의 표현력과 복잡한 패턴에 대한 적응력이 입증된 Fourier Neural Operator (FNO)의 아이디어를 따라, 컨볼루션 커널을 행렬 값 커널 (M)로 모델링합니다. 여기에서 N(노드) x d(차원) x d의 파라미터 크기로부터 대규모 그래프에 대한 오버피팅의 위험을 방지하기 위해, 모든 주파수 범위에 걸쳐 가중치 공유 방법을 도입합니다. 단일 MLP를 활용하여 d x d로 축소합니다.
• 위 방법들을 전부 통합시킨 WaveGC의 컨볼루션 연산은 식 10으로부터 공식화됩니다.

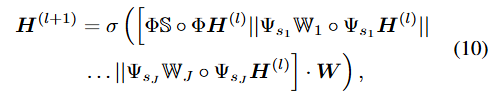
• 입력 임베딩 H^(l)에 대하여 J개의 웨이블릿 기저(Ψ=Ug(s_j*lambda)U^T) 및 행렬 값 기반 웨이블릿 커널 (W), 그리고 한개의 스케일링 기저(Φ=Uh(lambda)U^T) 및 행렬 값 기반 스케일 커널 (S)를 통해 변환된 신호들을 모두 concat합니다. 그 이후 MLP & 활성화 함수를 통과시키는 업데이트 흐름으로 진행됩니다.
• 원본 및 변환된 도메인 간의 신호 보존을 보장하는 Tight Frames를 만족시키기 위해, l₂ norm을 사용하여 h, g 함수를 정규화합니다. Tight Frames이 만족되게 되면, 푸리에 역변환을 단순히 변환 행렬의 역행렬을 통해 수행할 수 있게 되어 (U^T –> T^T) 계산 복잡성을 크게 낮추고 효율적인 컨볼루션 연산을 수행할 수 있게 됨을 언급합니다.

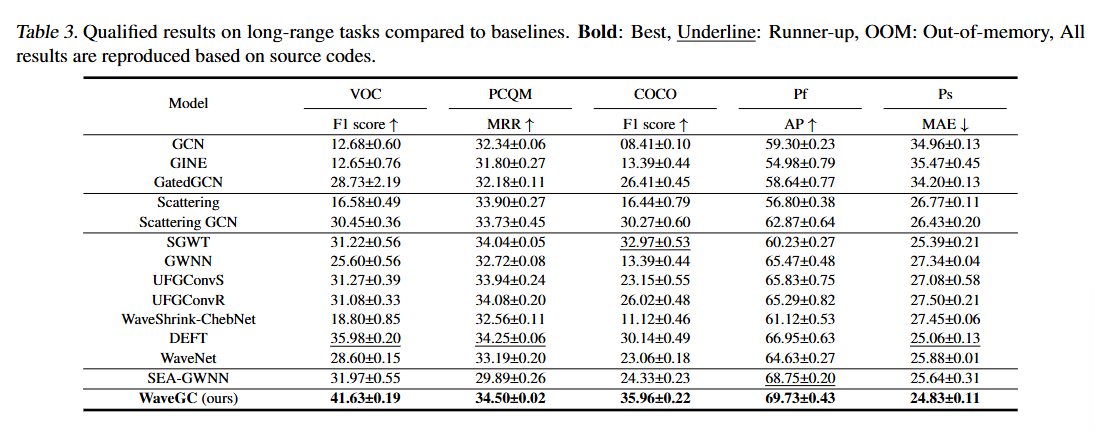
• 실험 결과는 WaveGC가 기존의 GNN, Graph Scattering Network, Spectral Graph Wavelet Network 및 Wavelet Lifting Transform 기반 다양한 모델에 비해 단거리 및 장거리 신호 데이터셋 모두에서 우수한 성능을 보임을 포괄적으로 입증합니다. 특히 PascalVOC-SP 데이터셋에서는 최대 11.83%의 상당한 성능 향상을 달성하여, 장거리 정보 인식 능력의 우월성을 보여줍니다.

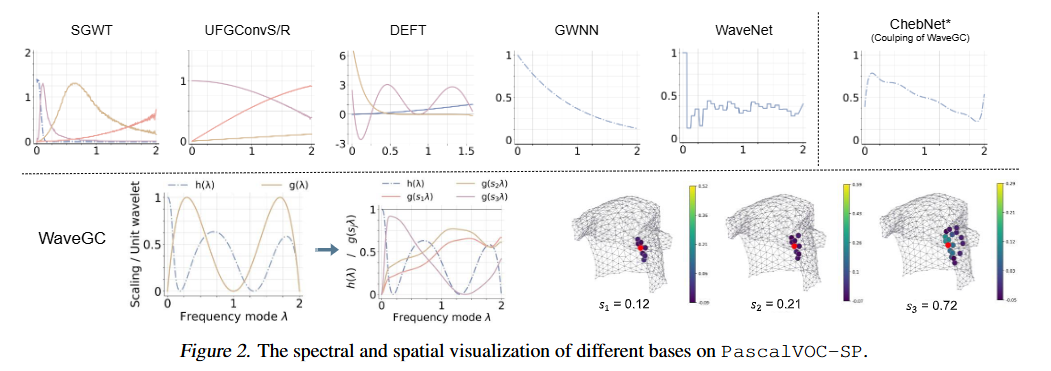
• 왼쪽 하단의 그림을 통해 WaveGC가 웨이블릿 허용 조건 및 Tight Frames을 만족하면서 더욱 유연한 스펙트럼 특성을 커버할 수 있으며, 우측 하단의 그림을 통해 학습된 스케일을 통해 Receptive field를 조절할 수 있어 다양한 데이터셋 시나리오 상에서 일관된 높은 성능을 얻을 수 있는 정량적 증거를 뒷받침합니다.

• 논문의 전체 내용을 한 문장으로 요약하면 다음과 같습니다.
  • 다중 해상도 스펙트럼 기저와 행렬 값 필터 커널을 통합한 새로운 웨이블릿 기반 그래프 컨볼루션 모델, WaveGC는 (이론적으로) Chebyshev 다항식의 홀수 및 짝수 항을 개별적으로 조합하여 웨이블릿 허용 기준을 엄격히 만족하는 학습 가능한 그래프 웨이블릿을 구축하며, (실험적으로) 다양한 데이터셋 시나리오 상에서 기존 다양한 그래프 스펙트럼 모델들을 일관되게 능가하는 성능을 보임으로써 단거리 및 장거리 정보를 효과적으로 포착하고 분리할 수 있는 WaveGC의 효과성을 입증하였습니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn