25년 8월 3주차 그래프 오마카세
Tensor-view Topological Graph Neural Networks
paper link :https://arxiv.org/abs/2401.12007
official code : https://github.com/TaoWen0309/TTG-NN?utm_source=catalyzex.com
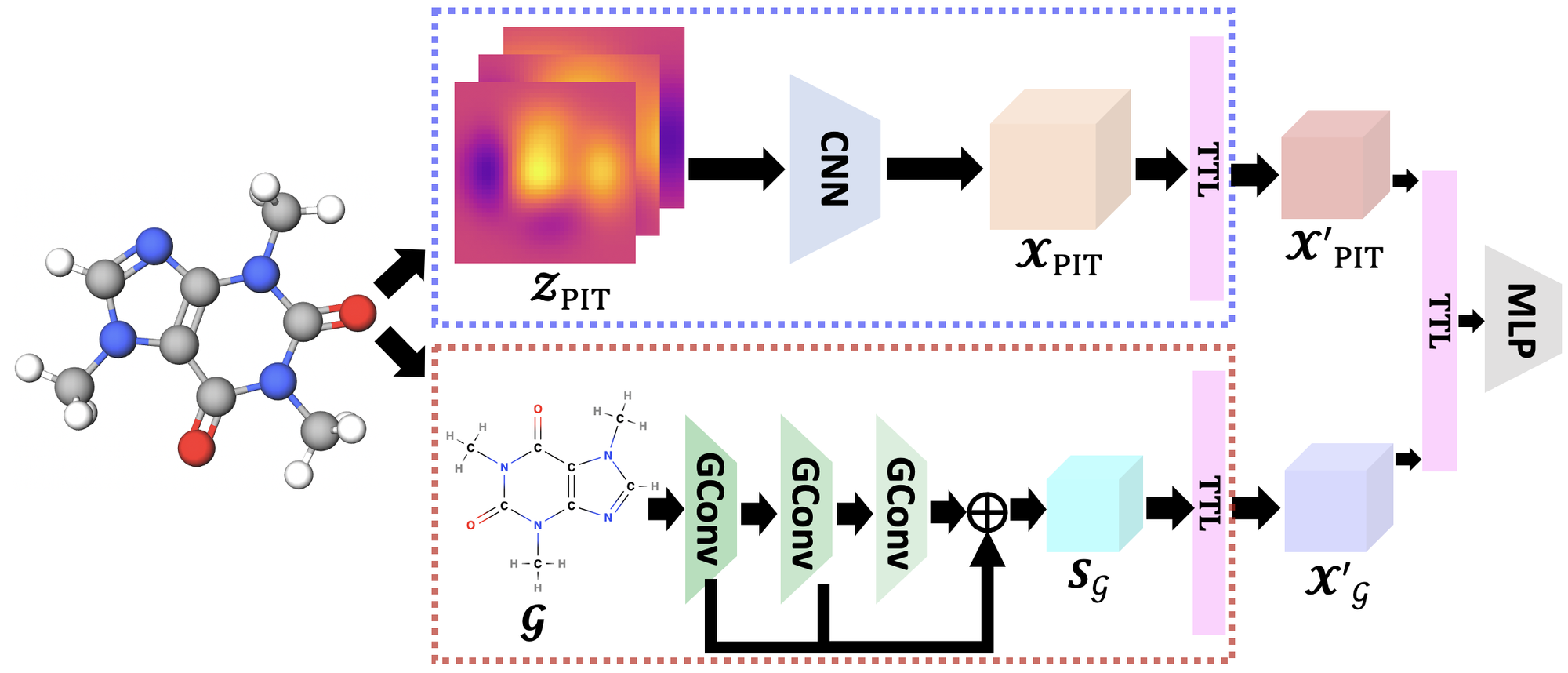
- 저번 주 오마카세로 전해드렸던 텐서 연산의 그래픽 이해를 바탕으로, 이번 주 가볍게 소개해드릴 논문은 텐서 학습을 통합하여 로컬 및 글로벌 레벨에서 Tensor-view Topology 정보와 Tensor-view Graph의 구조 정보를 동시에 포착하는 효과적인 토폴로지 딥러닝 방법론을 제안합니다.
- 그래프의 고차원 위상 구조(higher-order topological structures)나 다중 모달 정보를 포착하는 그래프 신경망을 그래프 분류 작업에 적용하고자 합니다. 다음을 위해 세가지 주요 모듈 (TT-CL, TG-CL, TTL)을 소개하고 있습니다.
- 위 모듈들은 위상 이론에서 주요 개념인 지속 호몰로지(Persistent Homology), 그래프 합성곱(Graph Convolution), 그리고 텐서 연산(Tensor Operations)을 키워드로 설계되었습니다.
- 그림에서 나타낸, 제안된 프레임워크 (TTG-NN)은 로컬 및 글로벌 텐서를 생성 및 조합하는 방향으로 크게 두 가지 핵심 구성 요소로 이루어집니다.
- 첫째, graph filtration를 통해 Tensor-view Topology feature를 추출하고, 이를 Tensor-view Topological Convolutional Layers (TT-CL, Sec 3.1) 모듈을 사용하여 local topological embedding을 학습합니다.
- 위 과정에서 첫번째 키워드, 지속 호몰로지가 활용됩니다. 구체적으로, 그래프 연결성의 다양한 수준에서 특정 위상 구조를 점진적으로 포착하기 위해서 다양한 노드 중심성 측정치(e.g. degree centrality score, closeness centrality score) 를 기반으로 여러개의 graph filtration 함수들을 활용합니다.
- 다중 스케일에서 그래프의 위상 정보를 응축한 표현의 지속 이미지 텐서 (Persistent image)를 CNN과 글로벌 풀링의 조합을 통해 숨겨진 위상 특징을 학습합니다.
- 둘째, 그래프 구조와 노드 특징을 활용하여 Tensor-view Graph 특징을 생성하고, 이를 Tensor-view Graph Convolutional Layers (TG-CL, Sec 3.2) 모듈을 통해 global structural features을 학습합니다.
- 랜덤워크 기반 정규화 인접행렬의 거듭제곱을 활용하여 multi-hop 정보를 수집하고 concat하여 노드 임베딩 텐서를 얻어냅니다.
- 고차원의 로컬 및 글로벌 텐서 정보는 그대로 활용하기에 연산량이 크다는 문제가 있습니다. 따라서 Tensor Transformation Layer (TTL, Sec 3.4)을 통해 저랭크 분해(low-rank decomposition)를 활용한 연산 효율성을 향상시킵니다.
- 여기에서 Tucker 텐서 연산의 저랭크 구조를 활용하여 코어 텐서 추정 오차를 크게 줄여준다는 이론적 보장을 제공합니다. 자세한 내용은 Sec 3.5 Provable Benefits of TTL with Tucker Low-Rankness 세션의 설명을 참고해주시기 바랍니다.
- 첫째, graph filtration를 통해 Tensor-view Topology feature를 추출하고, 이를 Tensor-view Topological Convolutional Layers (TT-CL, Sec 3.1) 모듈을 사용하여 local topological embedding을 학습합니다.
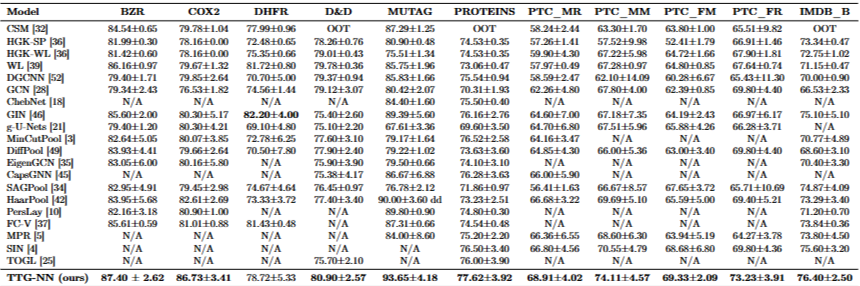
- Tensor Transformation Layer (TTL)에 Tucker 저랭크 구조를 통합함으로써 효율적으로 연산량을 줄일 수 있다는 이론적인 이점은 Sec.4의 폭넓은 실험을 통해 실증적으로 검증됩니다. Subgraph Matching kernel 계열, 일반적인 GNN, 그리고 그래프 풀링(pooling) 방법들을 포함한 총 20가지의 sota 모델들을 활용하여 11가지 그래프 분류 데이터셋에서 비교되었습니다.
- 주요 모듈들(TT-CL, TG-CL, TTL) 유무에 따른 ablation study 결과에서도 TTG-NN 구성에 필수적이며, 이들이 결합될 때 성능 향상 및 연산 효율성 측면에서 최적의 결과를 낼 수 있음을 보여줍니다.
- 결론적으로, TTG-NN은 그래프의 위상 및 구조적 특징을 텐서 형태로 통합하고 저랭크 텐서 분해를 활용한 TTL을 통해 효율적으로 학습하는 새로운 접근 방식을 제시합니다. 이는 기존 GNN의 한계를 극복하고 그래프 분류에서 최첨단 성능을 달성할 수 있었음을 보여주었습니다.
[Contact Info]
Gmail: jhbae1184@akane.waseda.jp
Twitter (X): @jhbae1184