25년 12월 3주차 그래프 오마카세

Comparing RAG and GraphRAG for Page-Level Retrieval Question Answering on Math Textbook

Comparing RAG and GraphRAG for Page-Level Retrieval Question Answering on Math Textbook

Technology-enhanced learning environments often help students retrieve relevant learning content for questions arising during self-paced study. Large language models (LLMs) have emerged as novel aids for information retrieval during learning. While LLMs are effective for general-purpose question-answering, they typically lack alignment with the domain knowledge of specific course materials such as textbooks and slides. We investigate Retrieval-Augmented Generation (RAG) and GraphRAG, a knowledge graph-enhanced RAG approach, for page-level question answering in an undergraduate mathematics textbook. While RAG has been effective for retrieving discrete, contextually relevant passages, GraphRAG may excel in modeling interconnected concepts and hierarchical knowledge structures. We curate a dataset of 477 question-answer pairs, each tied to a distinct textbook page. We then compare the standard embedding-based RAG methods to GraphRAG for evaluating both retrieval accuracy-whether the correct page is retrieved-and generated answer quality via F1 scores. Our findings show that embedding-based RAG achieves higher retrieval accuracy and better F1 scores compared to GraphRAG, which tends to retrieve excessive and sometimes irrelevant content due to its entity-based structure. We also explored re-ranking the retrieved pages with LLM and observed mixed results, including performance drop and hallucinations when dealing with larger context windows. Overall, this study highlights both the promises and challenges of page-level retrieval systems in educational contexts, emphasizing the need for more refined retrieval methods to build reliable AI tutoring solutions in providing reference page numbers.

arXiv.orgEason Chen

• 지난 오마카세에서 전달해드렸던 내용들을 통해, 기존 RAG에 비교한 GraphRAG의 차별성을 여러 번 전해드린 바 있습니다. 문서 전체를 아우르는 포괄적인 질문 및 전체적인 맥락 파악에는 GraphRAG가 강했으며, 단순 키워드 매칭으로는 찾기 힘든 멀티홉 연결 관계를 잘 포착해냈습니다.
• 하지만 "과연 모든 상황에서 GraphRAG가 정답일까?" 라는 비판적인 시각을 담은 논문 한편을 이번 주 오마카세로 전달해드리고자 합니다. 해당 저자들은 개념 간의 연결이 그 무엇보다 중요한 수학 교과서 데이터에 대해서, 통상적인 직관대로라면 수학의 복잡한 정리들을 연결해주는 GraphRAG의 강점을 기대해볼 수 있을 테지만, 실험적으로 오히려 기본적인 RAG가 더 높은 성능을 달성한 부분에 대한 구체적인 반증을 해당 논문에서 제시하고 있습니다.
• 정보의 풍부함을 기반으로 특정 페이지를 찾아 답변하는 정밀 검색 과제(Page-Level Retrieval)에서 오히려 노이즈로 작용할 수 있음을 보임으로써 무조건적인 최신 기술 도입보다는 중요한 데이터와 목적의 궁합의 중요성을 강조한 내용에 대해 가볍게 다루어보고자 합니다.

• 많은 사람들이 GraphRAG에 열광했던 이유는 명확합니다. 기존 RAG가 문맥을 뚝뚝 끊어먹을 때, 지식 그래프를 기반으로 정보 사이의 숨겨진 연결고리를 찾아주었기 때문입니다. 하지만 이번 연구는 바로 그 연결고리가 때로는 독이 될 수 있음을 날카롭게 지적합니다.
• 해당 논문에서 꼬집은 GraphRAG의 핵심 문제는 '과도한 정보 확장 (Excessive Content)' 입니다. 질문에 포함된 키워드(엔티티)와 연결된 이웃 노드들을 거치면서 정보를 수집하게 됩니다. 여기에서 문제는, 정답이 아주 구체적이고 좁은 범위에 있을 때에도 그래프 구조 상 연결되어있다는 이유만으로 불필요한 배경지식 또는 정보들까지 모조리 끌고 온다는 점입니다.
  • 쉬운 예시로, 피타고라스의 정리가 몇 페이지에 있는지와 같은 페이지 관련 검색 쿼리에 대해서, 피타고라스란 인물의 배경 및 그 제자들의 업적 등 까지 모두 고려하여 정작 원하는 페이지 번호를 헷갈려버리는 아이러니한 상황과 같습니다.
  • '너무 많이 아는 것이 병이다.' 라는 역설이 불러오는 노이즈 문제를 명확하게 드러내고 있습니다.
• 다음 문제점을 검증하기 위해, 저자들은 도메인 선정 및 차별화된 평가 방식을 선택하는 실험 환경을 설계했습니다.
  • 논리적 위계가 엄격하고, 답이 명확해야 하는 수학 도메인을 선택하여 학부 수학 교과서 맞춤형 벤치마크('An Infinite Descent into Pure Mathematics')을 구축함으로써, 대충 얼버무리는 답변은 요구하지 않는 엄격한 기준을 잡았습니다.
    •  해당 벤치마크 데이터셋은 GPT Vision 모델을 이용한 OCR 처리가 적용된 초기 628개 샘플에서 477개로 구성된 샘플들은 질문, 답변, 그리고 해당 질문이 포함된 교재의 특정 페이지로 구성됩니다.
  • 또한, 단순히 질문에만 대답하는 것을 넘어, 그 내용이 교과서의 어느 페이지에 있는지를 정확하게 찾도록 하는 평가 기준을 추가하였습니다. 이는 모델이 주변 맥락에 휘둘리지 않고 핵심 정보의 위치를 얼마나 정밀하게 맞출 수 있는지를 검증하는 가장 확실한 방법임을 밝히고 있습니다.

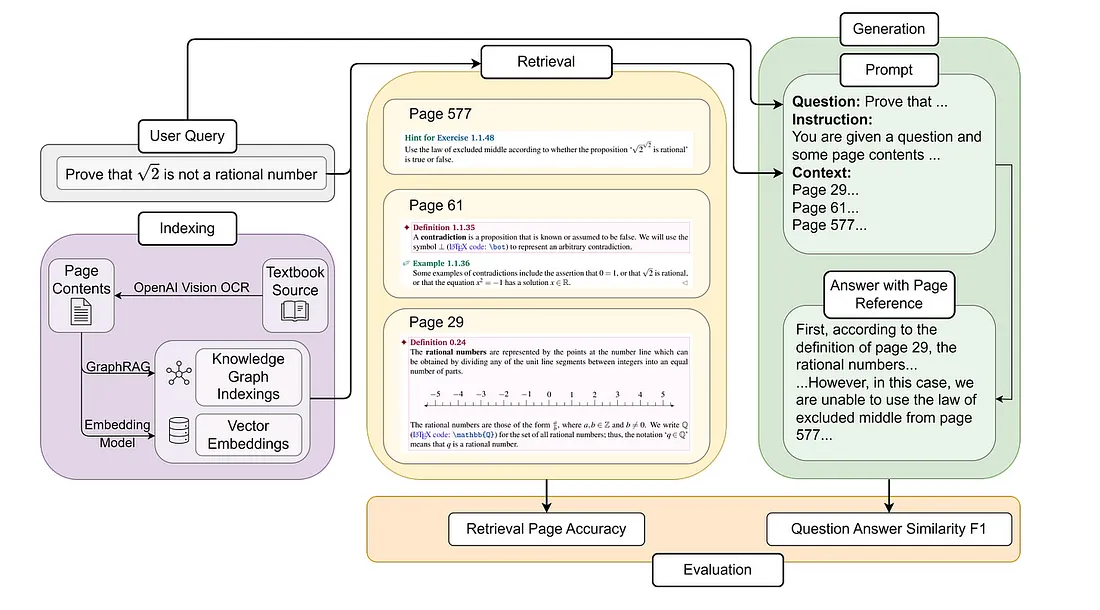
• 기본 RAG에서는 위의 간단한 3단계 작동 프로세스 (Indexing, Retrieval, Generation)를 기반으로 널리 사용되는 임베딩 모델 5가지를 테스트하였으며, GraphRAG의 경우 본질적으로 개념이 페이지를 넘나들며 어떻게 흐르는지를 모델링하기 위해 페이지 간 관계를 활용하도록 몇 가지 핵심적인 개선 사항을 설계하였습니다.

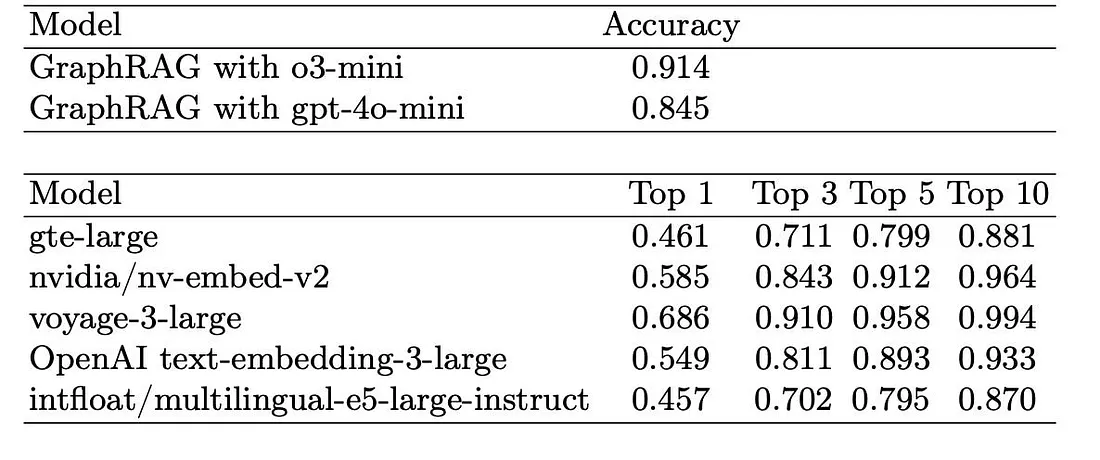
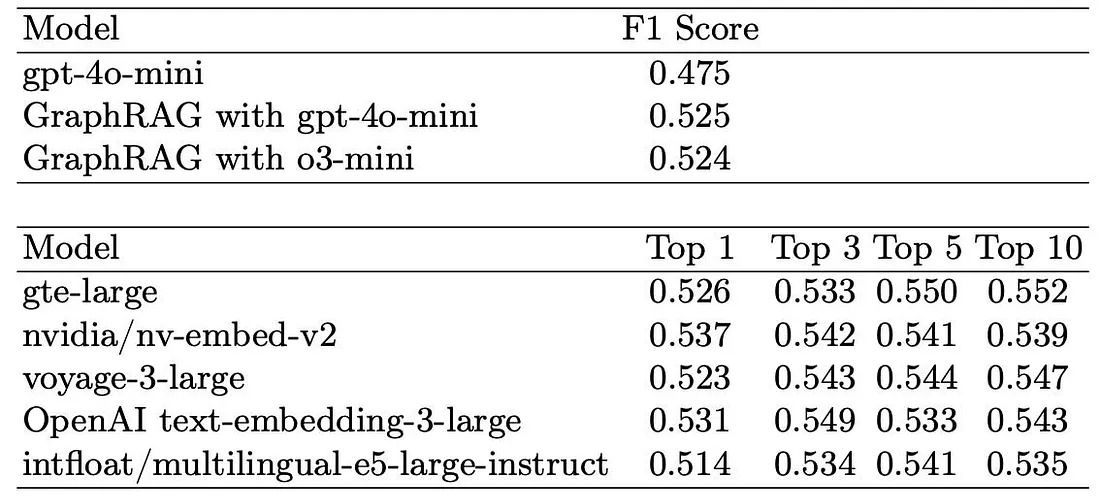
• 다음 실험의 결과는 기존 임베딩 기반 Standard RAG가 검색 정확도(Retrieval Page Accuracy, 올바른 페이지를 얼마나 자주 성공적으로 검색하는지를 측정) 및 답변 품질 (Question Answer Similarity F1, 모델의 출력과 정답 간의 일치도 측정) 지표를 기반으로 수행되었습니다.
  • 위 테이블은 엇갈린 결과를 보여주고 있습니다. 검색 정확도 측면에서는 매우 우수한 성능을 보이며, 최고의 RAG 모델들의 Top-3 성능과 유사합니다. 허나 생성된 답변에 대한 F1 점수는 대부분의 RAG 베이스라인에 비해 저조한 성능을 보입니다.
  • 핵심적인 문제점 중 하나는 중복성(Redundancy)입니다. GraphRAG는 가장 관련성이 높은 페이지뿐만 아니라 관련 엔티티까지 가져오기 때문에 직접적으로 도움이 되지 않는 추가 콘텐츠를 포함하는 경우가 많았습니다. 이러한 불필요한 추가 컨텍스트는 교과서 페이지 구조와 항상 잘 일치하지 않아 모델이 정확한 답변을 제공하기 어려웠습니다.
    • 벡터 유사도 기반 검색 중심의 RAG는 질문과 텍스트의 직접적인 유사성에 집중하기 때문에, 불필요한 맥락의 확장을 자제하고, 딱 필요한 정보가 있는 위치를 찾아내는 Precision 능력이 뛰어났습니다. 반면, GraphRAG는 엔티티 기반 구조 때문에 너무 많은 텍스트 chunk를 검색 결과에 포함시키면서 노이즈로 작용하는 문제점이 존재했습니다.
    • 이로부터 얻어낼 수 있는 결론은 명확합니다. 수학 교과서의 페이지 수준 질문 답변에는 현재로서는 전통적인 임베딩 기반 RAG가 더 나은 선택입니다. GraphRAG는 여전히 답변 생성 품질과 페이지 정렬에 어려움을 겪고 있어 전반적인 효율성이 제한적입니다.
  • 다음 측면에서 GraphRAG가 RAG의 상위 호환 버전이라는 고정적인 생각은 버려야 함을 시사합니다. 즉, 해결하고자 하는 질문의 유형에 맞춘 상호 보완적인 선택지로 고려해야 함을 알 수 있습니다.
    • 데이터 전체의 트렌드를 요약하거나, 탐구 및 추론과 같은 복잡한 질문인 경우에는 GraphRAG가 강력할 수 있으나, 특정 사실 및 규정 등 정해진 답을 정확하게 찾아야 하는 경우 RAG가 좋을 수 있음을 확인해볼 수 있겠습니다.

• 해당 논문으로부터 얻어낼 수 있는 인사이트와 개인적인 생각들을 아래와 같이 정리해보겠습니다.
  • 해당 접근의 Granularity은 Page-level입니다. 즉, 한 페이지에 대한 질문을 하고 그 페이지에 근거한 답변을 기대하는 것입니다. 하지만 GraphRAG의 그래프는 개념과 개념을 연결합니다. 이 차이에 포커스를 둔다면, 결론적으로 이번 실험의 패착은 Granularity의 불일치에 있다고 생각합니다. 구체적으로, 저자들은 페이지 단위의 정밀한 답변을 원했지만, 정작 GraphRAG는 거대한 지식 차원의 개념을 보여주려 했기 때문입니다. 이 불일치가 결국 노이즈를 만들었지 않았을까 조심스레 지적해봅니다.
    • 더 나은 접근 방식은 페이지 기반 특화된 그래프를 구축하는 것일 수 있습니다. 예를 들면, 각 노드는 각각의 페이지를 나타내고, 엣지는 구성 섹션들의 구조, 수학 공식들 간의 의존성 또는 참조된 페이즈 등등을 나타낼 수 있습니다. 그런 다음, 신뢰도가 낮을 ​​때만 인접 영역을 확장하여 노이즈를 줄이는 시도가 조금 더 효율적일 수 있지 않을까 생각해봅니다.
  • 또한, 정량적 평가가 단순히 정확도나 F1 점수에만 의존해서는 안 됩니다. 실제 실험 환경에서는 학습 효과와 참고 자료의 신뢰성이 더욱 중요할 수 있습니다. 즉, 인접 페이지 간의 연결성이 의미 있는지, 핵심 정의와 공식이 다루어지는지, 참고 자료의 일관성이 유지되는지 등을 더욱 구체적으로, 명시적으로 고려해야 합니다. 교육적 맥락에서 이러한 지표들이 검색의 진정한 가치를 더 잘 반영할 수 있다고 생각합니다.
• 독자 여러분들께서도 생각해보면 좋을 것 같은 포인트는, (감히 제안드려본다면), 단순히 GraphRAG가 성능이 낮더라 라는 결론보다, "왜 맞지 않았을까? 어떻게 해결해볼 수 있을까?"에 대한 근본적인 이유를 파고들어야 하는 점입니다.
  • 위의 불일치 문제로부터, 수학 도메인과 관련한 논리적 구조가 중요한 데이터에서는 그래프 구조가 추상적인 개념이 아닌 페이지 중심의 물리적 개념으로 설계 전략을 구축해보고, 그 효과를 기대해볼 수 있는 방법 (엣지 재정의, 노이즈 최소화 전략 등)을 고민해보는 것도 좋은 접근이라 생각합니다.
  • 또한 해당 도메인이 교육적 가치의 평가가 중요한 부분이라면, 기존의 단순 모델의 성능을 평가하는 정량적 지표(e.g. 정확도, F1 점수)만으로는 교육용 검색 품질을 온전히 담아내기 힘들 것입니다. 즉, 해당 도메인에서는 수치적 성능 평가가 아니라, 교육적 효과를 고려한 다양한 측면에서의 정량적 평가를 도입하는 것이 좋을 수 있습니다.
    • 예를 들면, 수학의 핵심 정의와 그 공식이 제대로 연결되었는지, 인접 페이지 간의 맥락이 교육적으로 유의미하게 연결되었는지, 또는 참고 자료들의 일관성이 잘 유지되는 지 등의 평가방식을 정량화하는 기준 마련이 중요할 것으로 생각합니다.
• 이러한 관련된 논문들을 읽어볼수록, GraphRAG는 도메인 최적화라는 다음 단계로 이제 막 진입한 것으로 보입니다. 무조건적인 최신 기술 도입보다는, 데이터의 구조와 사용 목적에 맞게 그래프를 재설계하고 적절한 RAG 기술을 도입하는 유연함이 필요한 시점으로 생각합니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn