25년 7월 1주차 그래프 오마카세
On Measuring Long-Range Interactions in Graph Neural Networks
paper link : https://arxiv.org/abs/2506.05971
official code : https://github.com/BenGutteridge/range-measure?utm_source=catalyzex.com
- 이번주 오마카세에서는 오랜만에 고질적인 메세지 전달 메커니즘의 한계인 장거리 종속성(long-range dependency) 포착 문제를 해결하는 새로운 방법론을 제안한 논문을 소개해드리고자 합니다.
- 다들 잘 아시다시피 오버 스무딩(over-smoothing) 및 오버 스쿼싱(over-squashing)과 같은 문제는 먼 거리에 떨어진 노드의 특징정보를 포착하는 능력을 저해합니다. 기존에는 Long Range Graph Benchmark(LRGB)와 같은 'Empirical' benchmark가 long-range capability를 검증하는 데 사용되었으나, 이는 이론적 근거가 부족하고 robustness가 떨어진다는 한계가 있습니다.
- 본 논문은 이러한 격차를 해소하기 위해 그래프 task에서의 long-range interaction 개념을 공식화하고, 그래프 상의 연산자(operator)를 위한 정량적인 범위 측정법(range measure)를 도입합니다. 그로부터 얻을 수 있는 본 논문의 주요 기여는 다음과 같습니다.
- Empirical heuristic이 아닌 기본적이며 기초적인 명제(first principle)에 기반한 long-range interaction의 정의 공식을 명시적으로 제시합니다.
- GNN의 long-range dependency를 포착하는 정도를 측정하는 공식적 및 정량적 측정도를 자세하게 유도하고 노드 및 그래프 레벨 tasks에 포괄적으로 적용 가능한 사실을 보여줍니다.
- Synthetic experiments를 통해 제안된 범위 측정도를 검증하고, 실세계 LRGB benchmark를 휴리스틱하게 분석하여 실제 long-range의 여부를 평가하는 기준을 제시합니다.
- 첫번째 기여 부분에서 중요한 부분은 범위 (range)에 대한 개념을 공식화하는 것입니다. 다음을 노드 및 그래프 레벨 문제의 두가지 카테고리 측면에서 접근하며, 이에 대한 핵심내용은 아래와 같이 요약할 수 있습니다. (본 논문의 Sec 3,4 참조)
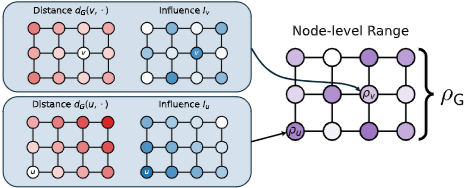
- 노드 레벨에서 범위 측정치는 "먼 노드들이 얼마나 강하게 상호작용하는지"를 포착하는 데 집중합니다. 저자들은 일련의 바람직한 속성을 만족하는 unique한 측정치로써 범위를 도출한다고 언급하고 있습니다.
- 그래프 각 노드 (u)에 대한 선형 맵 (F)의 범위를 측정합니다. 다음을 p_u(F)로 표기하며 Locality, Unit Interaction, Additivity, Homogeneity의 네가지 주요 그래프 속성들을 만족하는 유일한 measure로 유도됩니다.
- p_u(L)은 간단히 특정 u 노드의 출력에 대한 다른 노드 v의 거리와 맵핑 함수로부터 포착되는 상호작용 강도 (|L_uv|)의 곱을 모든 노드에서 합산하는 함수를 가리킵니다. (Theorem 3.1 확인)
- 짧은 거리의 두 노드 간 상호작용이 범위를 불균형적으로 증가시키는 문제를 해결하기 위해 마지막 2가지 속성(Addictivity, Homogeneity) 대신 새로운 속성 (Property 5 확인)을 도입하여 Normalized p_u(F)를 유도합니다. (Theorem 3.2 확인)
- GNN의 연산자 함수의 경우 미분 가능한 Jacobian 행렬을 기반한 범위를 아래의 공식으로 정의합니다.
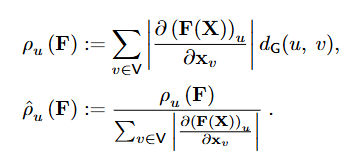
- 그래프 레벨의 경우, 위의 Jacobian 기반 p_u(F)는 task별 출력의 각 입력노드에 대한 Sensitivity만 포착하기 떄문에 pairwise interaction을 정의하는 데 부적합함을 언급합니다. 따라서 2차 Taylor expansion 항에서 나타나는 Hessian 행렬을 활용하였습니다.
- Hessian 기반 범위 (\nu) 및 normalized 형태 (\hat_\nu - 식 4 확인)는 아래의 공식들로 정의됩니다.

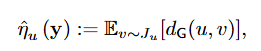
- 다음 정의는 Hessian 기반 분포 J_u(v)에 대한 거리의 기댓값으로 해석될 수 있음을 언급합니다. 다음 분포는 특정 노드 u가 다른 노드 v의 Feature 변화에 얼마나 민감하게 반응하는지를 정량화하며, 거리 지표로는 SPD (Shortest Path Distance) 및 Resistance Distance를 사용함을 밝힙니다.
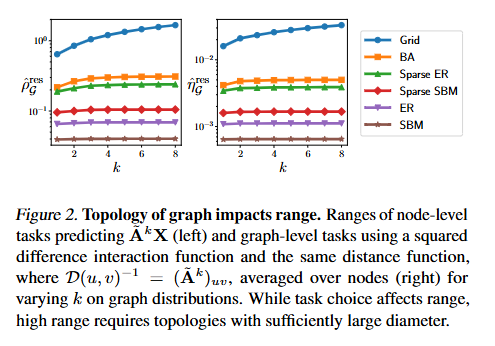
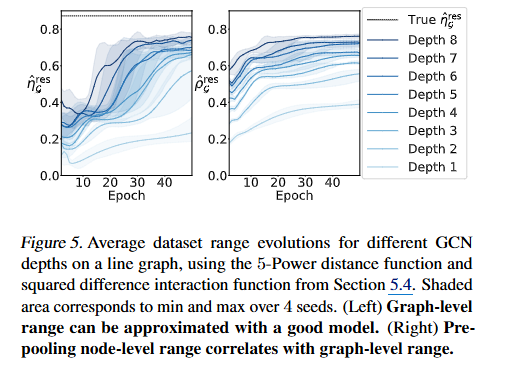
- 세션 5에서는 정의한 범위 측정방법이 실제로 어떻게 작동하는지에 대한 구체적 예시를 보여줍니다. 노드 및 그래프 레벨 태스크에 대한 다양한 실험 및 토폴로지에 대한 경험적 및 분석적인 결과들을 논의합니다.
- 경험적 결과에서는 Sparse topology와 높은 k 값은 더 큰 범위를 유발한다는 사실을 확인할 수 있었으며, 분석적 결과에서는 상호작용 범위가 넓어질수록 범위가 증가함을 이론적으로 보였습니다.
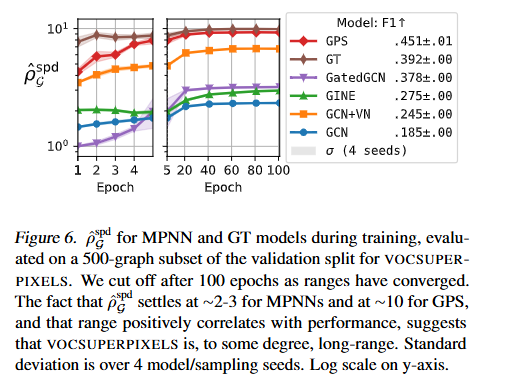
- 실험 세션에서는 Synthetic dataset으로부터 그로부터 잘 학습된 GNN (valid error -> 0)가 task의 true range를 근사할 수 있다는 사실을 검증하였습니다. Real world benchmark dataset (LRGB tasks)에서는 범위를 직접 알기어렵기 때문에 여러 아키텍처에 걸쳐 휴리스틱하게 GNN 성능과 범위 간 상관관계를 사용하였음을 언급합니다.
- 다음 논문을 정말 재밌게 읽었는데, 내용이 다소 어려워 이해를 위한 충분한 시간 투자가 필요하다고 생각됩니다. 하지만 그래프 ML 분야에서 중요한 토픽인 long-range 관련한 이해를 깊게 도와주고 새로운 아키텍처 및 벤치마크 테스트를 위한 인사이트를 제공하고 있다고 생각합니다. 독자 여러분들께서도 시간을 투자하셔서 찬찬히 읽어보시면 많은 도움이 되실 것 같습니다.
- 공식 코드도 제공하고 있습니다. 확인해보지는 못했으나 코드를 통해 핵심 아이디어를 쉽게 이해하실 수 있을 것 같으니 같이 참고해보시면 좋을 것 같습니다.
- 마무리하며 위 내용을 간결하게 요약해보았습니다.
- GNN의 long range interaction에 대한 개념을 '이론적'으로 공식화하고 정량적으로 측정하는 방법을 소개합니다.
- 제안된 범위 측정값은 Jacobian (노드 태스크) 또는 Hessian (그래프 태스크)을 기반으로 하며, 노드 간 거리에 따른 영향을 분석하여 작업 및 GNN 모델의 범위를 정량화합니다.
- 합성 데이터셋 및 실세계 LRGB 벤치마크 데이터셋에서 유효성을 확인하였으며 결과적으로 MPNN 및 GT 계열 모델에서 성능-범위 상관관계의 휴리스틱한 특성을 평가하였습니다.
[Contact Info]
Gmail: jhbae1184@akane.waseda.jp
Twitter (X): @jhbae1184