25년 7월 2주차 그래프 오마카세
Graph Representational Learning: When Does More Expressivity Hurt Generalization?
paper link : https://arxiv.org/abs/2505.11298
official code : https://github.com/RPaolino/GenVsExp
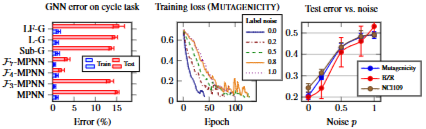
- 그래프 신경망(GNN)은 구조화된 데이터 학습에 매우 유용한 도구로 자리 잡았지만, GNN의 표현력(expressivity)과 실제 예측 성능(predictive performance) 사이의 관계는 여전히 명확하게 이해되지 못하고 있습니다.
- 보통 GNN 표현력은 WL 테스트 기반한 그래프 동형구조를 얼마나 잘 구별하는지를 측정합니다. 이론적으로 높은 수준의 WL 테스트를 통과하는 GNN은 강력한 표현력을 갖는다고 여겨집니다. 하지만 실제 작업에서 항상 더 나은 성능을 보이는 것이 아니라는 사실을 해당 논문에서 밝힙니다.
- 때로는 MPNN과 같은 1-WL 수준의 표현력을 가진 모델로도 많은 그래프 데이터셋에서 좋은 성능을 얻을 수 있습니다.
- 반대로 그래프 구조 정보를 거의 사용하지 않아 1-WL보다 표현력이 낮은 모델이 특정 작업에서 복잡한 GNN보다 더 뛰어난 성능을 보이기도 합니다.
- 그로부터 저자들은 아래의 두가지 중요한 질문을 독자들에게 던집니다.
- GNN에서 표현력이 증가하는 것이 성능 향상에 언제 도움이 되고, 언제 오히려 해를 끼치는가?
- 만약 더 표현력이 높은 GNN이 더 나은 성능을 보인다면, 이것이 단순히 그래프 구별 능력이 향상된 표현력 자체 때문인가?
- 질문에 대한 답변을 합성 및 실제 데이터셋 상에서 초기 실험 결과를 제시함으로써 GNN의 일반화 성능이 모델의 표현력과 데이터 자체에 내재된 구조-레이블 상관관계 사이의 적절한 균형에 달려 있다는 가설로서 도출합니다. 즉, 모델의 표현력이 데이터의 핵심 구조를 잘 포착하는 방향으로 작용할 때 일반화 성능이 향상된다는 것입니다.
- 자세한 방법론을 전해드리는 것 보다 논문의 기여점을 살펴보는 것도 충분할 것 같습니다.
- 위에서 제시한 가설을 경험적 통찰에 기반한 이론적인 정립 과정으로 풀어냅니다. GNN의 성능은 단순히 표현력이 높다고 결정되는 것이 아니라, 태스크에 관련한 구조적 특징을 기반한 유사성을 측정하는 능력으로 결정된다는 사실을 보입니다.
- 저자들이 제안하는 새로운 유사 거리를 통해 유사성 측정 능력을 정량화합니다. 제안 거리는 특정 그래프 불변량에 의해 파라메트릭하게 활용 가능하며, 그로부터 다양한 GNN의 표현력 수준을 포착할 수 있음을 언급합니다.
- 유사 거리가 가까운 두 그래프에 대해 동일한 레이블을 가질 가능성이 높다고 가정하고, 실제 그래프 학습 과정에 있어서의 일반화 성능에 얼마나 영향을 끼치는지를 경험적으로 분석합니다. 그로부터 위에서의 합성 및 실제 데이터셋을 활용한 이론적 분석을 뒷받침하며, 일반화가 모델 복잡도와 데이터의 태스크 관련 구조적 유사성 간의 섬세한 균형에 달려 있음을 보입니다.
- 해당 논문에서 저자들이 주장하는 핵심 내용은 표현력이 높은 GNN이 훈련 데이터가 충분하지 않거나 테스트 그래프와의 구조적 유사성이 낮을 때 일반화 성능이 저하될 수 있음과, 태스크에 최적화된 표현력을 갖는 GNN이 더 나은 일반화를 달성할 수 있다는 것입니다. 자세한 뒷받침 내용은 본문 내용 및 코드를 확인해보시면 좋을 것 같습니다.
[Contact Info]
Gmail: jhbae1184@akane.waseda.jp
Twitter (X): @jhbae1184