25년 7월 3주차 그래프 오마카세

Positional Encoding meets Persistent Homology on Graphs

paper link : https://arxiv.org/abs/2506.05814

official code : https://github.com/Aalto-QuML/PIPE

• 이번 주 오마카세에서는 그래프 표현 학습에서 중요한 모듈로써 활용되고 있는 '위치 인코딩(Positional Encoding, PE)'에 새로운 그래프 위상을 활용하는 점에서 제안된 논문을 소개해드리고자 합니다.
• 이웃 노드의 정보를 기반으로 업데이트가 진행되는 대다수의 메세지 전달 GNNs은 국소적인 inductive bias로 인해 연결성 및 사이클 등 입력 데이터의 핵심 구조정보를 활용하는 데 한계점을 드러냅니다. 다음 문제를 완화할 수 있는 방법으로 PE가 핵심 모듈로써 활용되고 있음은 다들 너무 잘 아시고 계실거라 생각합니다.
• 기존의 다양한 PE 방식들 (e.g. Spectral method - Graph Laplacian 행렬의 고유벡터/값 활용한 Global structure 파악, Relative distance - Randomwalk 기반 anchor node로 돌아오는 루트를 학습한 Structure 파악) 은 GNN 모델에 Location-aware feature를 부여함으로써 학습 효율성을 극대화합니다. 하지만 상대적인 효율성에 비해 그 바탕이 되는 이론적 특성화의 부족함을 해당 논문에서 언급합니다.
• 이론적 간극을 메우기 위해, 저자들은 수학적 이론이 탄탄한 지속 호몰로지 (Persistent Homology, PH) 개념을 적극 활용하고자 합니다.
  • 지속 호몰로지라는 개념이 GNN의 발전에 있어서 기존에 활용되지 않은 것은 아닙니다. 실제로 일부 연구들에서는 PH를 활용하면 추가적인 Multi-resolution topological features를 포착할 수 있는 강화성을 GNNs에 부여할 수 있음을 밝혔습니다. (`How well does Persistent Homology generalize on graphs?' , `Persistence Enhanced Graph Neural Network' 참고)
• 해당 논문에서, 저자들은 PE와 PH 중 어느 한 패러다임이 다른 패러다임보다 표현 능력이 우월하지 않다는 통찰력을 증명하는 새로운 구성을 제시합니다. Persistence-informed Positional Encoding (PiPE) 라는 이름의 새로운 학습 가능한 방법을 제안하였으며, 다양한 그래프 표현학습 도메인에서 강력한 성능을 입증합니다.

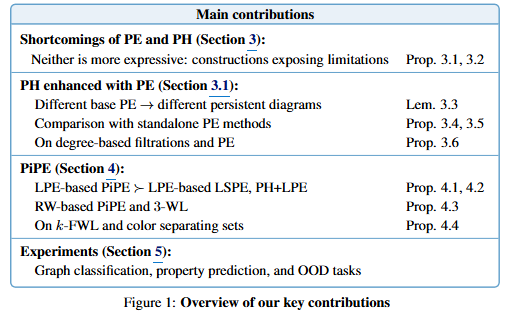
• Figure 1에서 보여주는 저자들의 핵심 기여점은 다음과 같습니다. 크게 2가지 카테고리로 나누어 이론적, 방법론적 통찰력을 제시합니다.

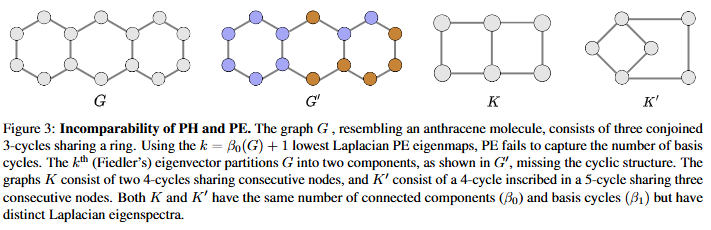
• (이론적) PE 및 PH 방법의 비교 불가능성과 그 한계, 그리고 이들을 결합하여 그래프 표현력을 향상시키는 방법에 대한 이론적 결과를 제시합니다. Figure 3에서는 Graph Laplacian PE의 핵심 구조포착 한계를 보여주면서, 그래프의 "위상적 특징 (Topological feature)"를 다양한 스케일에서 포착하는 PH를 활용하는 경우 이를 해결할 수 있다는 것을 보여줍니다.
  • 다음 통찰력을 통해, 저자들은 PE와 PH가 그래프의 서로 다른 측면을 포착한다는 사실을 밝힙니다. 즉, PE는 주로 노드의 위치 또는 국부적인 패턴에 강점을 가지는 반면, PH는 그래프의 연결성 또는 순환 구조와 같은 본질적인 형태 패턴을 포착하는 데 강점을 가집니다.
  • 따라서 어떤 한 방법만으로는 그래프의 모든 관련 구조 정보를 완전히 이해하기 어렵습니다. 이러한 비유성(Incomparability) 덕분에 두 방법을 결합하면 각자의 한계를 극복하고 더 강력한 그래프 표현을 얻을 수 있다는 것을 강조합니다.
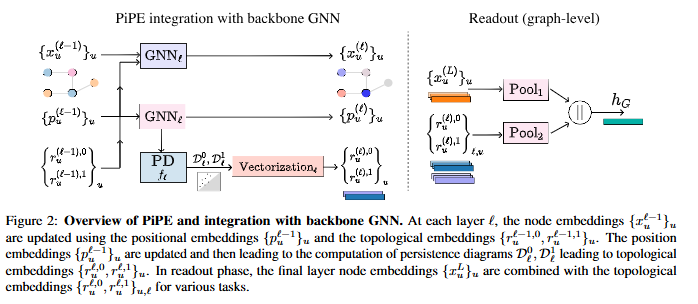
• (방법론적) 위의 이론적 통찰력을 바탕으로 Figure 2에서 나타낸 PiPE라는 새로운 PE+PH 방법을 소개합니다. 제안하는 PiPE는 Graph Laplacian PE(spectral) 및 Randomwalk PE (Relative dist)을 기반으로 구축되었기 때문에 임의의 메세지 전달 GNNs에 결합가능한 학습 가능한 LPE 모듈로써 그 유연성을 입증할 수 있음을 언급합니다.
• 임의 메세지 전달 GNNs에 통합 가능한 PiPE (Fig 2의 앞단)의 핵심 파이프라인은 다음과 같습니다.

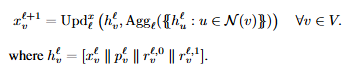
• 입력 그래프의 노드(x), 위치 특징(p), 그리고 그래프 구조에서 추출가능한 위상적 특징(r) 모두를 고려합니다. x 업데이트를 위해 {x, r} 특징 쌍에 대해 일반적인 GNNs의 메세지 전달 방식으로 학습을 진행합니다. p 업데이트는 단독적으로 일반적인 GNNs의 메세지 전달 방식으로 학습을 진행합니다 (식 5 참고).
• r 업데이트를 위한 {p, r} 특징 쌍에 대해선 먼저 일반적인 MLP를 활용한 지속 다이어그램(Persistent Diagram, PD)을 계산합니다. 여기에서 PD는 일종의 2D plane에 플롯된 점 집합으로써 직접적인 신경망에 입력으로 활용할 수 없기 때문에, TOGL에서 제안된 방법을 활용하여 이들을 벡터화합니다 (식 3,4 참고).
• 이후의 Readout 단에서는 최종 업데이트된 x, r를 결합하여 그래프 레벨 임베딩을 얻어내고 다양한 그래프 노드 레벨의 Downstream 작업에 활용합니다.

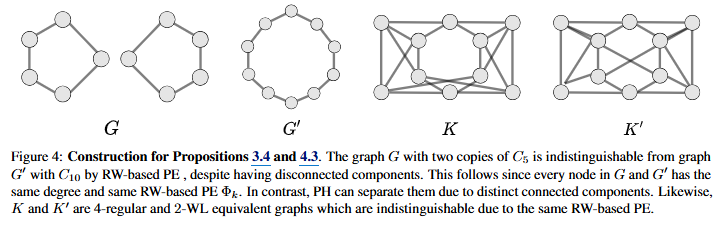
• Proposition 4.1. & 4.2에서 단순 PE (LSPE), PH + LPE에 비교한 LPE-PiPE의 이점을 분석하고, Figure 4와 같이 3-WL로 구분 가능한 RW-PiPE 결과를 제공합니다. 그래프 위상 활용의 강력한 정보 활용을 확인해보실 수 있습니다.

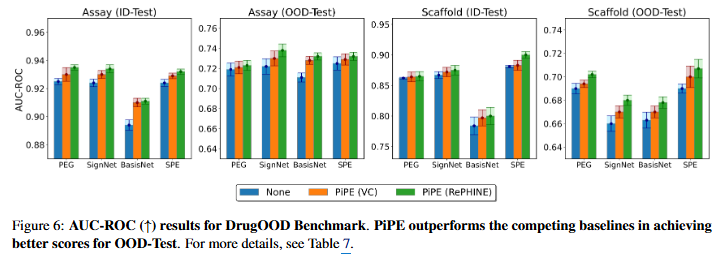
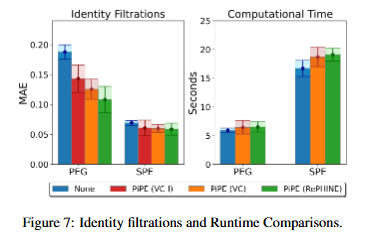
• Unattributed graphs (BREC dataset) & Drug, Molecule (Zinc, OGBG datasets ..), OOD(out of distribution, DurgOOD dataset), Synthetic Tree tasks의 포괄적인 실험을 통해 PiPE의 효과를 입증하고 기존 PE 방법들에 비해 상당한 개선을 보여주고 있습니다. 여전히 PH 임베딩 계산 비용의 높은 비효율성에 노출되어 있고, 최대 1차원 위상적 특징만을 고려할 수 없다는 한계점도 언급하며 차후 연구계획도 밝힙니다.
• 본 논문의 핵심 기여점들을 아래와 같이 요약해보면 다음과 같습니다.
  • 메세지 전달 GNNs의 귀납적 한계를 극복하는 다양한 PE 방법들의 이론적 한계를 PH를 통해 커버하고, 입력 그래프에 대한 핵심 구조적 특징을 포착하는 각자의 (실제, 상대적인) 장단점을 크게 2가지 통찰력 (이론적, 방법론적)으로 나누어 보였습니다.
  • 임의 메세지 전달 GNNs에 통합 가능한 PE + PH의 표현력을 결합하는 학습 가능한 LPE 모듈, PiPE를 제안하였습니다. 폭넓은 실험을 통해 다양한 노드레벨 그래프 태스크 상에서 단독으로 사용한 PE 및 PH 보다 더 높은 표현력을 보임으로써 그 일반화 성능과 성능적 우수성을 강조하였습니다.
• PiPE 공식 코드도 깔끔하게 정리되어 제공하고 있기 때문에 깊은 이해에 있어서 독자 여러분들께 좋은 참고가 될 것으로 생각합니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn