25년 7월 4주차 그래프 오마카세

Mitigating Over-Squashing in Graph Neural Networks by Spectrum-Preserving Sparsification

paper link : https://arxiv.org/abs/2506.16110

official code : https://github.com/Jinx-byebye/GOKU

• ICML 2025 논문 리스트업 중 그래프 스펙트럼 관점에서 오버스쿼싱 문제를 해결하는 새로운 Graph Rewiring 논문을 가볍게 리뷰 전달을 해드리고자 합니다. 국내 그래프 연구에서 빼놓을 수 없는 신기정 교수님께서 교신으로 참여한 연구인 만큼, 내용적으로나 결과적으로나 재밌게 접근해볼 수 있을 것 같습니다.
• 노드 업데이트가 반복적으로 더 많이 진행될수록, 고정된 크기 벡터의 한 노드에 흘러들어오는 주변 및 먼 노드의 메세지가 과잉되게 되면서 정보 압축 및 손실이 발생하는 현상을 오버스쿼싱 문제로 정의합니다. 다음 문제를 해결하는 대표적인 방법으로 그래프 토폴로지를 수정하는 리와이어링(Rewiring) 기법이 널리 사용되고 있습니다.
• 기존 리와이어링은 원본 그래프의 스펙트럼 특성 등의 중요한 속성을 보존하는 데 소홀하며, 연결성 개선을 위해 엣지 개수를 늘려 계산 오버헤드를 증가시키는 문제를 다음 논문에서 지적합니다.
• 제목 그대로, Spectrum-preserving graph sparsification 이라는 아이디어를 활용하여 새로운 그래프 리와이어링 방법, DSR를 제안합니다. 제안 방법은 연결성을 향상시키면서도 희소성을 유지하여 계산 오버헤드를 낮게 유지하고, 원본 그래프 스펙트럼을 대부분 보존하면서 구조적 병목 현상 감소와 그래프 속성 보존 사이의 균형을 효과적으로 맞출 수 있음을 언급합니다.
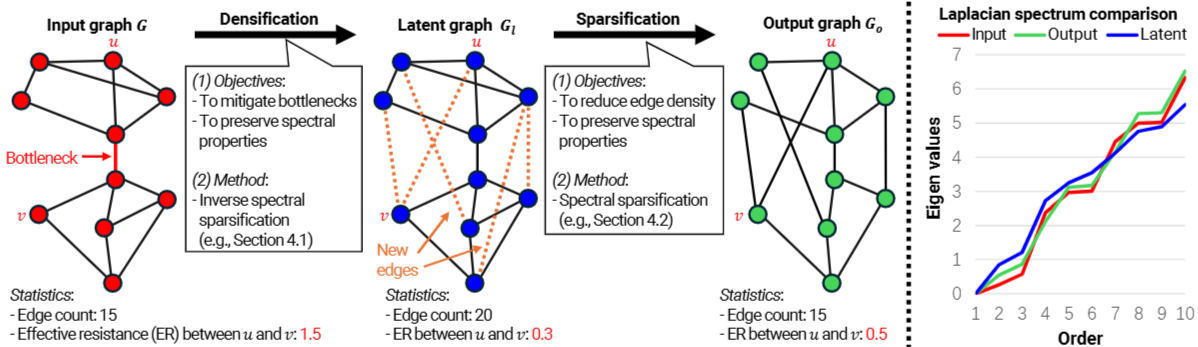
• 위 Fig 1에서 시각화한 Densification - Sparsification Rewiring(DSR) 패러다임은 GOKU(USS & ISS, Sec 4 참고)라는 방법론을 기반으로 크게 두 가지 순차적 단계로 구성됩니다.
  • Graph Densification : 병목 현상 및 중요한 스펙트럼 속성을 보존하기 위한 과정입니다. 입력 그래프 G를 잠재 그래프 G_l 의 스펙트럼 희소화 과정에서 주요 엣지들의 누락으로 인한 결과로 바라보고, Inverse Spectral Sparsification(Sec 4.1 참고)을 통해 이러한 누락 에지들을 복원하여 Densify시키는 방법으로 설명되어 있습니다.
    • 스펙트럼 속성을 유지하기 위해, Fiedler 벡터(그래프 라플라시안의 두 번째 작은 고유값에 해당하는 고유벡터)의 대수적 연결성(Algebraic Connectivity) 정보를 기반으로, 최대 우도추정 문제로써 Algorithm 1 (Unimportance-based Spectral Sparsification, USS)을 따라 공식화합니다.
• Graph Sparsification : 복원된 G_l 의 증가한 엣지 수로 인한 계산 복잡성 문제를 피하기 위해 Importance-Based Spectral Sparsification (ISS, Sec 4.2 참고)를 통한 연결성에 덜 중요한 엣지들을 선택적으로 제거함으로써 그래프 희소성을 유지하고자 합니다.
  • 노드 피처 간의 정규화된 코사인 유사도(S_e)를 기반으로 엣지의 유효 저항(Effective Resistance, R_e - 연결성의 강도)과 높은 유사도를 갖는 엣지를 우선적으로 유지하는 샘플링을 확률적으로 정의합니다 (p_e).
  • 유효 저항의 근사화 기법을 도입하여 노드 및 엣지 수에 대해 선형적인 스케일링을 보이는 시간 복잡도를 얻어낼 수 있습니다.

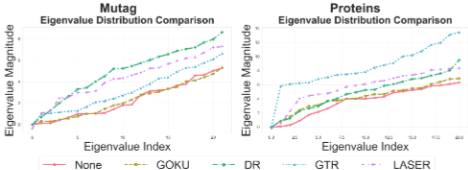
• 다양한 GNN 모델을 백본으로 10개 데이터셋에서 노드 및 그래프 분류 성능을 평가한 결과 다양한 리와이어링 기법의 성능을 능가함을 보였으며, 특히 heterophilic 그래프에서의 노드 분류 성능의 눈에 띄는 향상을 보였습니다.
• Fig 1의 Laplacian Spectrum comparison 그래프에서도 잠재 그래프 G_l의 고유값 분포를 따라 입력 G, 출력 G_o 의 스펙트럼이 매우 유사하게 유지되고 있음을 보여줌으로써, DSR 방법이 스펙트럼 속성을 효과적으로 잘 보존함을 확인할 수 있습니다.

• DSR (Graph Densification - Sparsification Rewiring) 방법을 통해 원본 그래프의 스펙트럼 속성을 보존하며 오버스쿼싱 문제를 완화하는 방법을 소개합니다. 두 가지 순차적인 단계의 목적성을 달성함으로써 주요 문제점인 병목 현상을 완화하고, 계산 오버헤드를 낮게 유지하면서 중요 스펙트럼 속성을 잘 유지하는 결과를 실험을 통해 입증합니다.
• 기존 리와이어링 기법보다 좋은 성능을 보인 사실로부터, 그래프 연결성 개선 뿐만 아니라 자체 특징을 잘 보존하는 균형을 효과적으로 맞추는 것의 중요성을 강조하였습니다. 여기에서 스펙트럼 희소화가 주로 가중 그래프에 의존한다는 점이 제한점으로 언급될 수 있지만, 대부분의 GNN 모델에서는 엣지 가중치를 자연스럽게 통합할 수 있어 실제 적용 시 큰 문제는 되지 않는다는 사실을 Limitations에 언급해두었으니 참고해보면 좋을 것 같습니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn