25년 6월 1주차 그래프 오마카세

이벤트 링크 : https://lu.ma/69ymean7

한정된 인원들만 참여가 가능하다보니, 신상이 불분명하신분들은 부득이하게 참여가 어려우실 수도 있습니다. 신청시에, 되도록 소속을 명확히 기입해주시면 감사하겠습니다.

추가로 정말 꼭 참여를 해보고 싶다 하신분들은 graphusergroup@gmail.com 으로 메일을 전달해주시면, 우선으로 자리를 배치해보도록 하겠습니다. 많은 참여 부탁드리겠습니다.

Plexus : Taming Billion-edge Graphs with 3D Parallel GNN Training

paper link : https://arxiv.org/abs/2505.04083

• 이전 오마카세에서 가볍게 소개해드린 것 처럼, 현재 AI 트렌드에 발맞춰 그래프 파운데이션 패러다임을 제대로 잡아나가기 위해서는, 우선적으로 제대로 구축된 대규모 그래프 데이터셋이 필요하다고 말씀드렸었습니다. 그리고 그에 맞는 대규모 그래프 학습 메커니즘 및 모델 설계가 따라와야만 합니다.
• 이런 흐름에 발맞추어 훌륭한 그래프 연구자분들께서 많이 작성해준 논문들 중에 정말 재밌고 유익한 방법들이 많이 쏟아지는 것 같습니다. 이번 주 오마카세에서는 대규모 그래프 학습 메커니즘 관련하여 새로운 3D 병렬 프레임워크를 제안한 논문의 최대 핵심 내용만 정리해서 전달해드릴까 합니다.
• 실제로 우리가 접하는 그래프들은 대부분 그 크기가 어마무시하기 때문에 GPU 메모리 용량을 초과하는 경우가 많아, Mini-batch sampling과 같은 처리 기법을 활용합니다. 그러나 다음은 정확도 저하, neighborhood explosion, CPU-GPU 데이터 전송 오버헤드 등의 여러가지 문제를 야기할 수 있습니다.
• 위의 문제를 해결하기 위한 새로운 방법론으로 분산 그래프 학습 메커니즘이 제안되었습니다. Distributed full-graph training 이름의 다음 메커니즘은 별도의 approximation 없이 학습을 수행하지만, 그래프의 불규칙한 구조로 인해 높은 통신 오버헤드 및 계산 로드 불균형 문제가 발생합니다.
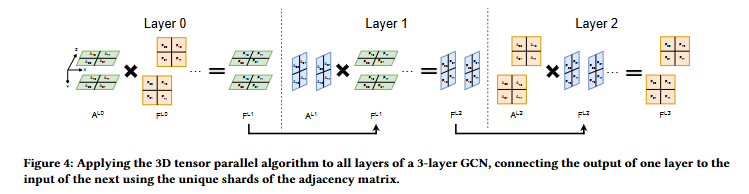
• 분산 그래프 학습 메커니즘의 문제점들을 해결하기 위해 제안된 Plexus 이름의 3D 병렬 프레임워크는 수십억(Billion) 개의 엣지를 가진 그래프까지 확장할 수 있습니다. 간단하게, 다음 논문의 3D 병렬 행렬곱셈 알고리즘을 GNN 학습에 맞게 개량한 것으로 볼 수 있겠습니다.
• Section 3에서는 3D 병렬화로 더욱 압축시켜 볼 수 있는 핵심 키워드의 방법론에 대해 GCN 레이어의 분산된(샤딩) 행렬 연산에 집중되어 설명하고 있습니다.

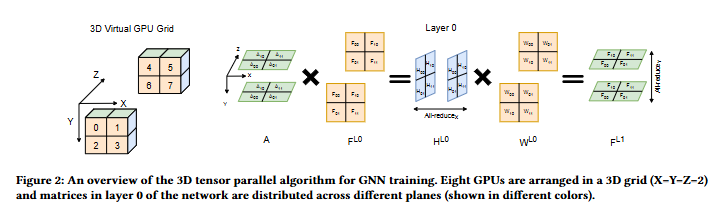
• G개의 GPU를 각 x, y, z 축으로 나누어 3D 가상 그리드로 구성하여 해당 채널 방향에 따른 통신 프로세스 맞춤형 그룹으로 나눕니다. 위 그림에서는 2 x 2 x 2 형태로 8개의 GPU가 구성되어 있으며, 각 GPU는 격자 내에서 3차원 좌표를 가지면서 이를 기반으로 통신 그룹을 형성합니다.
• 기본적으로 GCN의 레이어 L에서 입력 feature 행렬인 F과 sparse한 인접 행렬 A의 Sparse Matrix-Matrix Multiplication (SpMM)로부터 얻은 H 행렬에 대하여, 가중치 행렬 W과의 Dense MM (SGEMM) 연산으로 진행되는 것은 다들 잘 아시고 계실겁니다. 해당 SpMM 및 SGEMM 표기를 잘 기억해주세요.
• 각 통신 그룹에 대하여, 첫번째 레이어에서 인접 행렬 A, 특징 행렬 F^L0 , 그리고 가중치 행렬 W 각각에 대하여 독립적인 축 평면 및 여분 채널 축에 특정 크기로 샤딩(sharding)시킵니다. 샤딩된 A, F에 대하여 SpMM 연산 결과로 얻은 H와 샤딩된 W와의 SGEMM을 수행하여 F^L1 을 얻습니다.
• 다음 F^L1은 활성화 함수를 거쳐 다음 레이어의 입력으로 사용됩니다.
• 한눈에 볼 수 있는 포워드 & 백워드 알고리즘은 아래와 같습니다.

• 여기에서 All-reduce는 분산된 데이터를 모아 모든 GPU에 동일한 값을 분배하는 통신 연산입니다. X 및 Y 축으로 해당 연산을 수행하여 각 GPU가 필요한 정보를 공유합니다.
• Section 4에서는 Plexus는 최적의 3D 구성을 선택하기 위한 방법론을 설명합니다. SpMM 연산의 계산 시간 및 통신 시간을 예측하는 성능 모델을 포함하고 있습니다. 여기에서 계산 모델은 SpMM의 이론적인 FLOPs 뿐만 아니라 행렬 모양에 따른 SpMM의 비효율성을 반영하는 패널티항을 포함하고 있습니다.

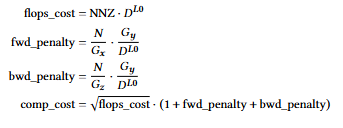
• Section 5에서는 성능 최적화를 위한 몇 가지 도입된 기법들을 설명합니다. 먼저 인접 행렬 A의 로드 불균형을 완화하기 위해 Double Permutation 기법을 사용합니다. 이를 통해 non-zero 원소의 분포를 효과적으로 균일화합니다.
  • 일반적인 GCN의 차수 행렬을 활용한 A의 정규화 항과 같은 개념으로 제안된 것으로 이해했습니다. 해당 식을 보면, 레이어에 따라 행 순열 (Pr) 및 열 순열 (Pc)의 순서를 다르게 적용하여 PAP^T 형태의 행렬을 만들어 사용합니다.

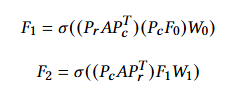
• 또한 SpMM 시간 변동성 문제를 완화하기 위해 Blocked Aggregation 기법을 적용합니다. 다음은 A를 작은 블록 행렬들로 나누어, 각 블록에 대해 순차적으로 SpMM 및 All-reduce 연산을 수행합니다.
  • 다음은 통신 오버헤드를 줄이면서, 특히 transposed 입력에 대한 SGEMM 연산의 효율성을 개선했다고 합니다.
  • 그로부터 대규모 데이터셋을 대상으로 Parallel Data Loading 유틸리티를 제공하여 CPU 메모리 사용량 및 로딩 시간을 크게 줄였습니다.

• 실제로 다음 Plexus는 슈퍼컴퓨터에서 다양한 대규모 그래프 데이터셋을 사용하여 평가되었습니다. 그로부터 많은 수의 GPU에 대한 뛰어난 확장성 및 낮은 abs epoch 시간을 보였습니다.
  • Perlmutter 슈퍼컴에 대해 최대 1024 GPU, Frontier 슈퍼컴에 대해 최대 2046 GCDs까지 확장 가능함을 보이며, 현재까지 보고된 full-graph GNN training 규모 중 가장 큰 규모를 갖게 됩니다.
  • 또한 기존 방식 최대 12.5배 빠른 학습 속도 및 최대 54.2배 짧은 time-to-solution을 달성하였고, 3D 병렬성과 최적화를 통해 안정적인 확장성을 보였습니다.
• 위 내용을 3줄로 요약하면 아래와 같습니다.
  • Plexus는 방대한 그래프의 메모리 및 계산 문제 해결을 위해 분산 전체 그래프 GNN 훈련을 위한 새로운 3D 병렬 프레임워크를 제안합니다.
  • 이 프레임워크는 3D 병렬 알고리즘, 로드 밸런싱을 위한 이중 순열, 그리고 최적의 훈련 구성을 예측하는 성능 모델을 특징으로 합니다.
  • Plexus는 최대 2048개의 GPU/GCD에서 수십억 에지 그래프로 확장 가능하며, 기존 최신 방법보다 크게 향상된 속도와 효율성을 보여줍니다.
• 엄청난 규모의 대규모 그래프에 대해 pruning 또는 approximation 없이 효율적이고 실용적인 full-graph GNN training을 가능하게 한 점에서 그 기여도가 상당히 크다고 생각되며, 앞으로의 그래프 파운데이션 관련 프론티어 연구 결과로 많이 언급되지 않을까 생각해봅니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn