GraphOmakase

25년 3월 3주차 그래프 오마카세

A Generalization of the Persistent Laplacian to Simplicial Maps

paper link : https://arxiv.org/abs/2302.03771

Key Contents

What is Simplicial Maps?
What is Persistent Laplacian?
Persistent Laplacian for Simplicial Maps (Generalization)

이번 주는 오랜만에 토폴로지 관점에서 그래프 상의 고차 관계성 (Higher-order relationship)을 분석하고 최적화하는 방법 관련한 이론적 논문 내용을 요약하여 전달해드리고자 합니다.
- 논문 제목을 보시면 아시다시피, Simplicial maps에 대한 지속 라플라시안의 일반화된 형태를 정의하고 이들의 속성을 수학적으로 풀어 설명하는 내용이 주라고 보시면 되겠습니다.
이번 오마카세에서는 Simplicial maps과 Persistent Laplacian의 개념과 그 일반화 방법에 대한 핵심 인사이트 내용들만 뽑아서 정리해드리고자 합니다.
꽤 예전에 제가 몇 주간에 걸쳐 전달해드렸던 토폴로지 신호 처리 (Topological Signal Processing) 내용과 연관이 있는 내용입니다. 당시 호지 라플라시안 (Hodge Laplacian) 행렬을 사용하여 Simplicial Complex (SC)라는 고차 관계성 (Higher-ordered relationship)을 인코딩하는 (확장형) 그래프 구조 상의 신호 흐름을 처리하는 이론적인 방법을 정리해드린 적이 있었습니다.
- 호지 라플라시안, 또는 조합 라플라시안 (Combinatorial Laplacian), 은 노드 간의 관계성을 포착하는 그래프 라플라시안의 능력을 고차 정보까지 확장시켜 일반화한 행렬로써 정의될 수 있습니다. 즉 노드, 엣지, 면 상에 흘러가는 신호 공간 "내" 개별적인 관계성 뿐만 아니라, 신호 공간 "간"의 복합적인 상호성까지 고려할 수 있다는 장점을 강조했었습니다.
이번에 소개해드릴 지속 라플라시안 (Persistent Laplacian)은 호지 라플라시안의 일반화 행렬로써 정의되어질 수 있습니다. 위의 " " 관계를 고려해보면, 호지 라플라시안의 SC "내" 관계성 뿐만 아니라 다른 SCs "간"의 관계성까지 포착하는 것으로 받아드릴 수 있겠습니다.
다음 내용을 이해하기 위해서 Simplicial Map이 무엇인지, 지속 라플라시안은 어떻게 정의되는지, 그리고 어떻게 일반화 시키는 지 에 대해서만 (간략하게) 설명드리면서 마무리하겠습니다. 해당 내용은 위 논문을 기반으로 전달되어집니다.

What is Simplicial Map?

Simplicial Map은 무엇일까요? 이름에서부터 짐작가듯이, 두 Simplicial Complexes (SCs) 간의 맵핑(Mapping)을 정의하는 연산자로 이해할 수 있을 것 같습니다.

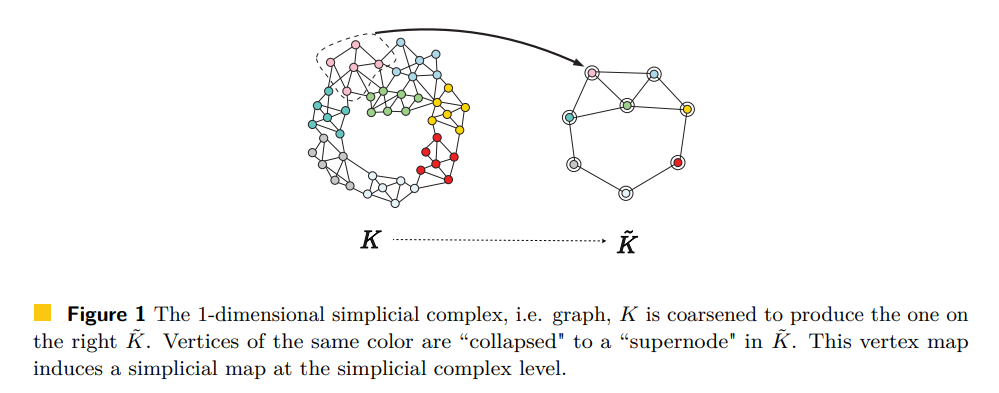
Fig 1에서는 임의의 SC, K로부터 동일한 레이블끼리 클러스터링한 (일종의 hypergraph 꼴) SC, K_tilde로의 맵핑을 표현하고 있습니다. 해당 맵핑 후의 그래프 구조가 sparsify (or coarsening)해지는 효과 덕분에 K 기반의 연산량 문제를 어느정도 완화하면서, 여러 사례에 대한 K_tilde 기반 적용성이 향상될 수 있음을 가볍게 언급합니다.
- 즉, 하나의 SC "상"의 정보를 고려하는 것도 중요하지만, 두 SCs "간"의 맵핑으로 얻을 수 있는 (실용적인) 효과도 무시할 수 없기 때문에 적절한 맵핑 정의가 요구되어진다 ! 를 첫장에서 언급합니다.
해당 맵핑은 선형 맵핑 (Linear map) 및 포함 맵핑 (inclusion map)의 두 연산자를 전적으로 기반하고 있습니다. 여기에서 포함 맵핑이란 한마디로 해당 SC의 "부분공간 (subspace)" 으로 맵핑하는 모든 연산자를 가리킵니다.
- 즉, Simplicial map은 본래 SCs 간의 선형 맵핑 뿐만 아니라, 그 하위공간으로의 포함 맵핑, 그리고 하위공간 간의 선형 맵핑이라는 복합적인 구성으로 정의되어집니다. 아래의 교환 다이어그램을 참고하시기 바랍니다.

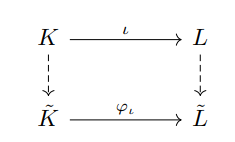
Bold arrow : linear mapping/ Dotted arrow : inclusion map

일반화를 위해 SC 구성 요소에 가중치가 존재하며 맵핑 전후의 다음 정보가 보존되는 두 SCs를 고려합니다. Weight preserving이라는 표현을 사용하는데 수식은 생략하고, 의미 그대로 받아들이셔도 무방합니다.
구체적인 이해를 위해, 전체적인 SCs를 바라보지 말고 이들을 구성하는 요소들 (simplex라고 부릅니다.)에 집중해봅시다. 그리고 이러한 요소들을 기저로 구성되는 선형 벡터공간인 체인 군 (Chain group, C)을 고려합시다.

Recaps to basics of simplicial complex

C_q^K 표기는 K라는 SC 속의 q차 simplex로만 구성된 체인 군의 의미로 생각해주시기 바랍니다.

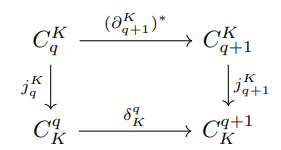
두 체인 군을 선형 맵핑하는 연산자로 바운더리 연산자 (Boundary operator)가 존재합니다. 바운더리 연산자의 역할은 한마디로 맵핑 이전의 체인 군에 속하는 q차 simplex보다 1차수 낮은 q-1차 simplex에 해당하는 이후 체인 군에 연결시켜줍니다.
- e.g. 면 (q=2) -> 바운더리 -> 엣지 (q=1) -> 바운더리 -> 노드 (q=0).
그에 대한 코체인 바운더리 (A^'*'기호)는 그 반대로 1차수 높은 q+1차 simplex에 연결시켜주는 역할로 생각하시면 됩니다.

다음 기본적인 개념들을 기반으로, oriented된 q차 simplexes으로 구성된 두 SCs (K, L)에 대하여 Simplicial map은 해당 체인 군 (C_q^K,C_q^L) 상에서 식 4와 같이 정의됩니다.

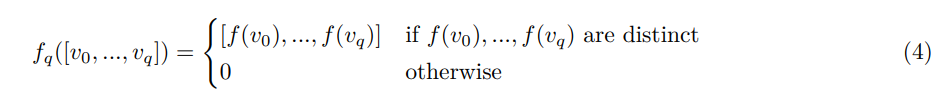
여기에서 oriented는 노드 인덱스의 오름차순 방향으로 방향성을 갖고 있음을 의미합니다.
식 4로부터 f_q기호의 Simplicial map은 C_q^K 상의 모든 q차 simplexes에 대하여, C_q^L 체인 군 상의 "동일한" 차수의 simplexes로의일대일 맵핑 함수로써 정의됩니다.
Oriented 방향성까지 고려하기 위해 sgn 함수를 추가합니다. 해당 함수는 맵핑 전후의 simplexes가 같은 방향성을 갖는다면 +1, 다른 방향성을 갖는다면 -1을 반환합니다.

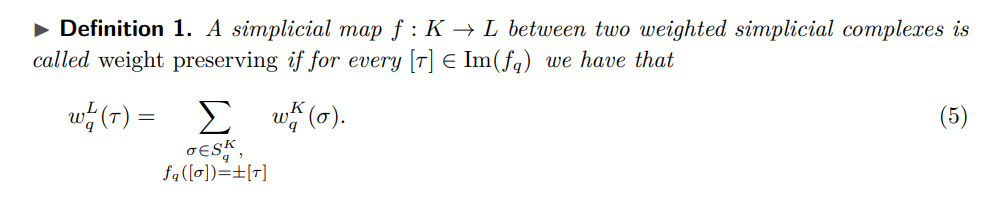
Simplical map은 weight preserving을 만족합니다.

💡

Simplicial map이란, 두 SCs, K와 L에 대하여 각걱의 체인 군 C_q^K의 모든 simplexes에 대해 C_q^L 상의 동일한 차수의 simplexes로의 일대일 맵핑 연산을 의미한다.

What is Persistent Laplacian ?

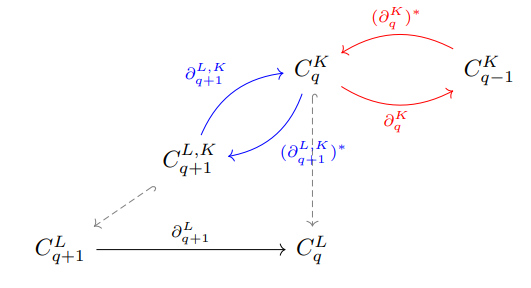
위의 Simplicial maps을 기반으로 Persistent Laplacian의 교환 다이어그램을 위의 그림으로 나타낼 수 있습니다. 복잡해보이는데, 해당 라플라시안 정의를 위해서는 파란색 및 빨간색 화살표만 고려하면 됩니다.
- 전자의 경우 두 체인 군 C_q+1^L,K와 C_q^K 간의 관계성을, 후자의 경우 C_q^K와 C_q-1^K 간의 관계성을 인코딩하는 것으로 보입니다. 직관적으로 K와 L "간"의 관계성 및 K "내" 관계성을 내포하고 있음을 이해할 수 있습니다.
- 두 관계성을 인코딩하는 라플라시안 행렬을 각각 '상위(up) 지속 라플라시안 ' 과 '하위(down) 지속 라플라시안'으로 정의하며, 이들의 합을 통해 아래의 식과 같이 지속 라플라시안을 정의합니다.

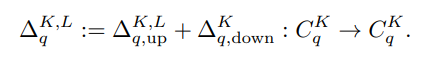
즉, 지속 라플라시안은 SC 내의

상위 지속 라플라시안을 정의하기 위해서 고려해야 하는 새로운 체인 군 C_q+1^L,K는 무엇을 의미하는 것일까요? 식 9에서 다음을 정확하게 정의합니다.

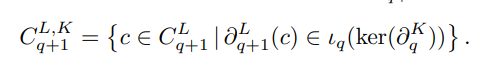
i_q : C_q^K -> C_q^L의 Simplicial map 기호와 동일합니다.

위 식에서 알려주는 해당 체인 군 정의와 관련 정보들은 다음과 같습니다.
- C_q+1^L,K 의 정의 : "C_q+1^L 체인 군 상 "의 특정 simplexes, c에 대하여 그 바운더리가 "C_q^K와 관련한 어떤특정 공간" 속에 포함되는 경우를 만족하는 것들의 집합으로 정의되는 체인 군.
  - C_q+1^L,K는 C_q+1^L의 하위공간이다. 즉, C_q+1^L은 우리가 이미 알고 있는 체인 군이기 때문에 다음의 포함 맵핑을 통해 손쉽게 정의가능함.

다음 특정 공간은 C_q^K -> C_q-1^K=0 을 만족하는 C_q^K의 하위공간이 i_q 함수를 통해 맵핑된 C_q^L 의 하위공간과 일치함.

상위 지속 라플라시안의 핵심 인사이트는 두 SCs "간" 관계성을 포착한다는 점인데, 그 관계성은 바로 (SC의 토폴로지 관점에서) L과 K의 지속성 호몰로지 와 동일합니다.
- 다음 인사이트는 L의 특정 simplex에 대한 바운더리 simplex가 다른 K의 kernel 공간과 연관되어지는 사실로부터 지속성 호몰로지 정의와 깊은 연관성을 갖게 됩니다.

💡

지속 라플라시안 (Persistent Laplacian)은 그 정의에 따라, 하위 지속 라플라시안의 SC "내" 관계성 뿐만 아니라 상위 지속 라플라시안의 SCs "간" 관계성까지 포착할 수 있으므로 기존 호지 라플라시안을 일반화할 수 있습니다.

핵심 인사이트는 상위 지속 라플라시안의 정의로부터 두 SCs의 지속성 호몰로지 특성을 포착할 수 있습니다.

Persistent Laplacian for Simplicial Maps (Generalization)

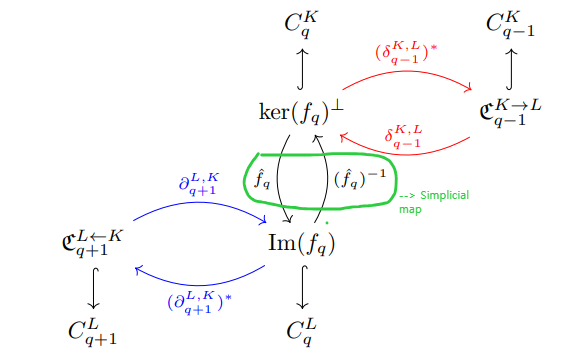
Simplicial maps 기반 지속 라플라시안의 일반화를 위한 교환 다이어그램 수정

다음 교환 다이어그램은 지속 라플라시안의 교환 다이어그램에서 그 정의의 기반이 되는 포함 맵핑의 복잡성을 제거하고, 직관적인 선형 벡터공간 맵핑만을 기반으로 수정한 다이어그램 입니다.
Simplicial maps의 정의에 복합적인 포함 맵핑 개념이 존재하지 않기 때문에 이를 지속 라플라시안 개념과 통합하기 위한 수정 다이어그램 정도로 이해하셔도 될 것 같습니다. 그로부터 기준 공간에 따라 아래와 같이 대체 정의가 가능한 장점을 부여하여 기존의 지속 라플라시안의 포함 맵핑 기반 단방향적 한계를 극복할 수 있습니다.

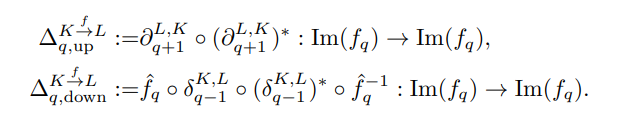
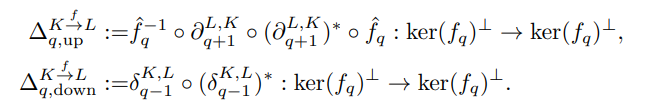
더욱 자세한 설명은 복잡성을 위해 생략하지만, 간략하게 Simplicial maps 과정을 연두색 부분과 같이 C_q^K 및 C_q^L의 하위공간 (kernel, image) 상으로 제약하고, C_q-1^K 및 C_q+1^L의 새로운 하위공간 상에서 상위 (파란색 화살표) 및 하위 (빨간색 화살표) 지속 라플라시안을 아래와 같이 정의하여 그 합산으로부터 일반화 지속 라플라시안을 정의합니다.
일반화 지속 라플라시안에 대한 핵심 특성들을 본 논문의 설명으로 대체하겠습니다.

💡

Our definition of persistent Laplacian generalizes the inclusion-based persistent Laplacian.

The two different definitions have their own advantages. Seeing the persistent Laplacian as an operator on Im(f_q) increases the interpretability of this operator as the matrix representation can be computed using the canonical basis of Im(f_q).
On the other hand, seeing the persistent Laplacian on ker(f_q)^⊥ helps us understanding some of its properties more easily.

이 이후의 해당 논문내용은 정의된 일반화 지속 라플라시안을 추가적으로 다양한 머신러닝 과제에 활용하기 위한 Schur Restriction 기반 행렬 표현 방법을 제시합니다.
또한 일반화 지속 라플라시안 계산 알고리즘 복잡도 및 상위 및 하위 라플라시안 각각의 고유값 기반 신호 스펙트럼의 특징들을 논의합니다. 결과적으로 기존 지속 라플라시안보다 연산 효율성 및 안정성 모두 확보할 수 있다는 사실도 강조합니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184