25년 9월 2주차 그래프 오마카세

Towards Quantifying Long-Range Interactions in Graph Machine Learning: a Large Graph Dataset and a Measurement

Towards Quantifying Long-Range Interactions in Graph Machine Learning: a Large Graph Dataset and a Measurement

Long-range dependencies are critical for effective graph representation learning, yet most existing datasets focus on small graphs tailored to inductive tasks, offering limited insight into long-range interactions. Current evaluations primarily compare models employing global attention (e.g., graph transformers) with those using local neighborhood aggregation (e.g., message-passing neural networks) without a direct measurement of long-range dependency. In this work, we introduce City-Networks, a novel large-scale transductive learning dataset derived from real-world city roads. This dataset features graphs with over $10^5$ nodes and significantly larger diameters than those in existing benchmarks, naturally embodying long-range information. We annotate the graphs using an eccentricity-based approach, ensuring that the classification task inherently requires information from distant nodes. Furthermore, we propose a model-agnostic measurement based on the Jacobians of neighbors from distant hops, offering a principled quantification of long-range dependencies. Finally, we provide theoretical justifications for both our dataset design and the proposed measurement - particularly by focusing on over-smoothing and influence score dilution - which establishes a robust foundation for further exploration of long-range interactions in graph neural networks.

arXiv.orgHuidong Liang

• 이번 주 오마카세로 소개해드릴 논문은 장거리 상호작용 (Long-range interactions)을 정량화하는 새로운 시도를 제시한 내용입니다. 기존 연구들은 주로 "Global attention을 사용하는 모델 (그래프 트랜스포머)이 MPNNs모다 성능이 좋다" 라는 간접적인 비교에 의존하여 장거리 상호작용 현상을 평가하였으나, 더 직접적인 측정방법을 제시하여 모호함을 완화하고자 하였습니다.
• 다음 논문에서 소개하는 데이터셋은 City-Networks로써, 실제 도시 도로에서 파생된 대규모 전이 학습 데이터셋을 의미합니다. 10만개 이상의 노드를 갖는 기존 벤치마크 셋보다 훨씬 큰 그래프 특성을 포함하고 있으며, 장거리 상호작용을 이해하는 것에 특화된 테스트 환경을 제공합니다.
  • 특히 노드 레이블이 Eccentricity를 기반으로 주어졌는데, 이는 멀리 떨어진 노드들의 정보가 그래프 태스크에 필수적인 특성을 보장하기 때문에 해당 논문의 주요 포인트로 작용합니다.
• LRGB 등의 작은 그래프에 초점을 맞추어 깊은 통찰을 제공하기 어려웠던 한계점을 해결하며, 도시 네트워크의 내재적인 장거리 정보 추출의 중요성을 기반으로 해당 도전과제에 대한 접근성을 집중시킵니다.

• 해당 저자들은 model-agnostic한 측정 방법을 제안합니다. 다음은 간단하게, 학습된 모델에서 Jacobian 행렬을 기반으로 특정 노드예측에 대해 다른 홉에 있는 이웃 노드들의 영향력을 정량화합니다.
• 단순히 모델의 성능 차이를 비교하는 것은 하이퍼파라미터 튜닝 등에 의해 결과가 왜곡될 수 있어 장거리 의존성을 명확히 평가하기 어렵습니다. 하지만 Jacobian 행렬 기반 측정은 모델의 내부 메커니즘을 통해 노드 간의 실제 정보 흐름과 영향력을 직접적으로 측정하여, 장거리 의존성의 존재와 강도를 보다 원칙적으로 파악할 수 있도록 돕습니다. 많은 관련 연구들에서 해당 행렬을 많이 활용하는 이유가 드러납니다.

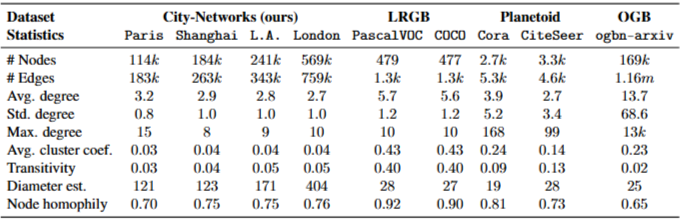
• City-network 데이터셋은 기존 citation network와 다른 토폴로지를 갖는 격자 형태의 도로망 구조를 가지고 있으며, 기존 LRGB의 inductvie learning이 아닌 Transductive learning 학습 방식을 띄고 있습니다. Spectral GNNs의 활용 가능성이 높을 것으로 예상되는 데이터셋이며, Eccentricity 기반의 노드 라벨링을 기반으로 도시의 접근성 연구 등의 실용적인 활용이 가능할 것으로 예상됩니다.
• 그래프 생성과정 및 노드 별 피처는 생략하고, 노드 라벨링에 대하여, Eccentricity 근사값을 활용합니다. (식 1 참고) 즉, 각 노드에서 가장 먼 노드 까지의 최단 경로거리를 활용하는데 다음은 전체 그래프를 고려하는 데 계산량 문제가 발생하기 때문에, 16-홉 이웃노드까지만 고려하여 그 연관성을 강조하는 데 집중하였습니다. 그리고 근사값을 10개의 quantile로 나누어 라벨링을 수행하였습니다.

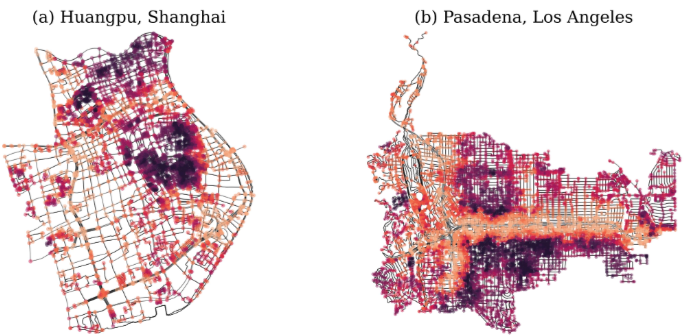
• City dataset 일부 도로망의 eccentricity 추정치를 시각화한 이미지입니다. 색상의 밝음 정도에 따라 크고 작음을 나타냅니다. 즉, 밝을 수록 eccentricity 값이 커서 접근성이 낮고 노드 간 거리가 멀다는 것을 의미합니다.
• 나타난 두 도시 모두에서 상당 부분의 그래프 토폴로지에 격자 형태를 갖고 있음이 확인됩니다. 다음은 해당 데이터셋 주요 특징 중 하나로, eccentricity를 노드 레이블로 사용하는 분류 작업에서 해당 데이터셋에 대한 신경망 모델의 장거리 상호작용 학습에 적합한 구조를 제공합니다.
• 위에서 언급하였듯이, 장거리 상호작용의 직접적 정량화를 위해 Jacobian 행렬을 기반으로 Infuence Score를 계산합니다. 특정 노드의 예측에 대한 타 노드들의 영향력을 분석하고 떨어진 거리에 따른 그 변화성을 분석하는 데 초점을 맞춥니다. (식 2 참조) 이에 대한 자세한 이론적 입증은 Sec 6를 참고해주시기 바랍니다.
  • Jacobian 행렬은 출력에 대한 입력의 Sensitive를 인코딩하고 있는 행렬로써, 즉 행렬 값들은 입력 노드 피처가 이웃 노드의 임베딩에 미치는 영향력을 나타냅니다.
  • 각 hop 거리별 영향력을 합산 후 평균을 계산하여 Average Total Influence (식 3 참조)를 계산합니다. 또한 평균적으로 다음 영향력이 얼마나 멀리까지 미치는지를 측정하기 위한 Size of Receptive Field도 계산합니다. (식 4 참조)
• 이론적 근거를 제시합니다. 다양한 기준값들을 가지고 Simple GCN 모델을 사용하여 오버스무딩 현상을 관찰하였는데 diameter가 크고 sparsitiy가 높은 City dataset에서 상대적으로 덜 발생함을 보였습니다.
• 또한 격자 형태의 그래프에서 이웃 노드 수 증가에 따른 평균 영향력이 약해지는 문제(Dilution)를 다루었는데, h-hop shell (Def 6.5 참고) 의 크기 증가에 따른 정도를 분석합니다. 평균 영향력보다 총 영향력 (Sum) 측정방법이 장거리 상호작용 측정에 더 적합하다는 사실을 보입니다.

• 그래프 학습 분야에서 중요한 장거리 상호작용 현상에 집중된 데이터셋 및 Jacobian 기반 직접적인 정량화 방법을 제안하였습니다. 자세한 설명 및 정량화 방법에 대한 이론적 근거 등을 Appendix를 통해 자세히 제공하고 있어 그 타당성을 충분히 뒷받침하고 있습니다.
• 일부 한계점들도 제시하였습니다. Sec 6.2에서 Jacobian의 절대값을 통해 절대적인 영향력에 집중하는 방식이 개별 노드의 Sensitivity를 높게 측정하지만 최종 출력에는 큰 차이가 없을 수 있다는 출력 상쇄(Output Cancellation) 문제를 잠재적으로 발생시킬 수 있다는 부분을 설명합니다. 다음은 정규화되지 않은 선형 모델에서 피처 간 높은 동시선형성 (colinearity)이 존재할 때 그 가능성이 높음을 언급합니다.
  • (Prop 6.1) MPNNs의 경우, 저자들은 정확 상쇄 (Exact cancellation)의 극단적으로 발생할 확률이 낮을 것이라고 설명합니다.
  • 즉, 해당 한계점을 통해 모델의 영향력 이해에단순한 Jacobian 값이 아닌 그 방향성도 고려하는 것이 중요할 수 있다는 사실을 시사합니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn