25년 9월 3주차 그래프 오마카세

GraphMETRO: Mitigating Complex Graph Distribution Shifts via Mixture of Aligned Experts

GraphMETRO: Mitigating Complex Graph Distribution Shifts via Mixture of Aligned Experts

Graph data are inherently complex and heterogeneous, leading to a high natural diversity of distributional shifts. However, it remains unclear how to build machine learning architectures that generalize to the complex distributional shifts naturally occurring in the real world. Here, we develop GraphMETRO, a Graph Neural Network architecture that models natural diversity and captures complex distributional shifts. GraphMETRO employs a Mixture-of-Experts (MoE) architecture with a gating model and multiple expert models, where each expert model targets a specific distributional shift to produce a referential representation w.r.t. a reference model, and the gating model identifies shift components. Additionally, we design a novel objective that aligns the representations from different expert models to ensure reliable optimization. GraphMETRO achieves state-of-the-art results on four datasets from the GOOD benchmark, which is comprised of complex and natural real-world distribution shifts, improving by 67% and 4.2% on the WebKB and Twitch datasets. Code and data are available at https://github.com/Wuyxin/GraphMETRO.

arXiv.orgShirley Wu

GitHub - Wuyxin/GraphMETRO: GraphMETRO: Mitigating Complex Graph Distribution Shifts via Mixture of Aligned Experts (NeurIPS 2024)

GraphMETRO: Mitigating Complex Graph Distribution Shifts via Mixture of Aligned Experts (NeurIPS 2024) - Wuyxin/GraphMETRO

GitHubWuyxin

• 최근 연구실 세미나에서 소개받은 논문으로, Graph Neural Networks(GNN)가 실제 그래프 데이터의 복잡하고 이질적인 분포 변화에 일반화하는 문제를 해결하기 위해 Mixture-of-Experts(MoE) 아키텍처를 조합한 새로운 아이디어를 제안하고 있습니다.
• 개인적으로 MoE에 대해 잘 모르기에 자세하고 정확하게 내용을 이해하는 것이 많이 어려웠습니다만, 제목에서와 같이 다루고자 하는 일반화 문제점을 MoE의 장점을 활용하여 복잡한 그래프 분포 변화를 완화하는 방향의 해결 프로세스가 꽤나 흥미로운 것 같습니다. 연구실원의 발표 자료를 참고하여 아이디어 핵심 및 GraphMETRO 제안 프레임워크의 워크플로우 정도만 간략하게 전달해드리고자 합니다. 다음 주제에 관련해 관심있으신 독자분들은 더욱 정확하고 깊은 이해를 위해 직접 해당 논문과 코드를 참고해보시는 것을 추천드리고 싶습니다.

• 그래프 데이터는 본질적으로 복잡하고 이질적이며, 이로 인해 다양한 유형의 자연적인 분포 변화가 발생합니다. 기존에 제안되어왔던 ML 아키텍처는 이러한 실제 세계의 복잡한 분포 변화에 효과적으로 일반화하는 데 어려움을 겪고 있습니다.
• GNN 측면에서의 일반화 연구는 주로 데이터 증강(data augmentation)이나 불변 표현(invariant representation) 학습에 초점을 맞추고 있습니다. 하지만 단순한 증강으로는 타겟 데이터가 특정한 패턴의 변화 유형을 따른다고 가정하며, 실제로는 알 수 없는 복합적인 변화를 갖는 경우가 많기에 적절하지 못합니다. 또한 불변 예측자를 학습하는 일반적인 전략은 조합적으로 너무 많은 분포 변화를 다뤄야 하는 어려움에 직면하고 있습니다.
• 이 논문은 GraphMETRO를 제안하고 있습니다. 이는 그래프 데이터의 자연적인 다양성을 모델링하고 복잡한 분포 변화를 포착하는 GNN 아키텍처로써, 복잡한 분포 변화를 여러 변화 요소 (shift component)로 분해하고, 타겟 데이터에서 관찰되는 그래프 이질성(heterogeneity)에 적응할 수 있는 예측기를 학습하는 새로운 프레임워크입니다.
  • 핵심 아이디어는 분해된 변화 요소들을 처리하기 위한 계층적 MoE (Mixture-of-Experts) 아키텍처를 사용하는 것입니다. 각각의 전문가 모델은 특정 변화 구성 요소를 목표로 하며, 참조 모델에 대한 불변 표현을 생성합니다.

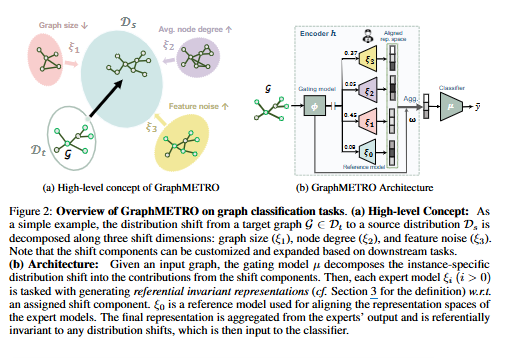
• Fig 2는 실제 그래프 데이터에 존재하는 복잡한 분포 변화를 어떻게 접근하는지 개념적으로 설명하기 위한 GraphMETRO 모델의 핵심 개념과 아키텍처를 보여줍니다.
  • (a)에서 여러 종류의 변화 요소들이 혼합되어 원본 그래프 데이터 분포에 다양한 변화가 나타날 수 있음을 보여주고 있습니다. 여기에서는 그래프 크기, 평균 노드차수, 그리고 노드 특징의 노이즈에 따른 분포 변화를 보여주고 있습니다.
  • 이러한 요소들의 개별적인 조합들로 분해하여 다양한 변화에 강건하게 대응할 수 있는 아키텍처가 (b)에 나타나 있습니다. 해당 아키텍처는 크게 Gating model 및 Expert model의 두가지 계층적 모델구성으로 이루어져 있습니다.
    • GNN 기반 Gating model은 분해된 요소들의 기여도를 가중치 벡터로 출력하는 역할을 담당하고 있으며, expert model의 출력에 대한 상대적인 중요도를 나타냅니다.
    • 해당 가중치를 기반으로 각 Expert model은 특정 요소들에 대응하게 되며, 입력 그래프에 아무런 변형이 가해지지 않았을 때의 표현을 학습한 참조 모델의 인코딩 표현과 유사한 표현을 얻는 것을 목표로 하여, 공통된 표현 공간에 모든 Expert model이 정렬되도록 강제합니다(Mixture of Aligned Expert).

• (Assumption 1 참고) 원본 분포와 대상 분포사이의 모든 K개의 분포 변화는 최대 k가지의 확률적 변환이 각 인스턴스에 적용된 결과로 모델링될 수 있다는 비공식적 가정을 기반으로 복잡한 변화에 대해 더 단순한 개별 구성 요소로 분해할 수 있다는 아이디어를 전개합니다. 그로부터 알려지지 않은 분포 변화를 그래프 샘플링 또는 가우시안 노이즈 추가 등의 여러 데이터 외삽 (extrapolation) 기법을 통해 여러 개의 이동 요소(shift components)로 분해합니다. 이 분해된 요소들은 각각 고유한 통계적 특성을 가지며, 원본 그래프에 적용되는 확률적 변환 함수(stochastic transformation functions)로 정의됩니다.
• GraphMETRO는 여러 이동 요소들을 처리하기 위해 계층적 아키텍처로 설계되었습니다. Gating Model은 입력 그래프에 가장 큰 영향을 끼치는 이동 요소들의 혼합을 나타내는 가중치를 출력합니다. Expert model은 각각 하나의 이동 요소에 대응되어, 참조 모델의 표현을 따라 불변 표현 (Referential Invariant Representation)을 생성하는 것을 목표로 학습됩니다. 결과적으로 모든 Expert model의 출력 임베딩 공간이 참조 모델을 통해 공통 표현공간으로 정렬되는 프로세스를 구성하게 됩니다.
• Gating model의 출력 가중치와 각 Expert model가 생성한 불변 표현들을 기반으로 최종 표현을 집계합니다. 다음은 Softmax를 적용한 가중 합으로 계산되며, 예측 작업을 위한 분류기의 입력으로 사용됩니다.

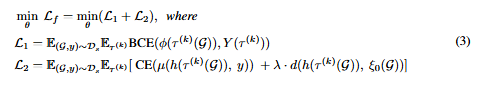
• GraphMETRO의 학습 목적 함수는 계층적 모델들의 최적화를 담당하는 두 가지 손실함수 (L1, L2)를 결합한 꼴로 정의됩니다. 각 손실함수는 Gating model이 이동 요소에 따른 분포 변화의 혼합을 잘 식별하고, Expert Model이 해당 변화에 불변하는 표현을 생성하면서 공통된 참조 공간에 잘 정렬되도록 지도하여 최종적으로 다운태스크 분류 작업의 성능을 향상시킬 수 있습니다.
  • L1은 원본 분포에서 샘플링된 그래프와 k개 이하의 변환 요소들로 구성된 임의의 확률적 변환 집합에 대해, 각각의 출력이 해당 요소들의 혼합된 구성을 정확하게 예측하도록 이진 교차 엔트로피(BCE)를 사용합니다. Gating model의 학습을 통해 최적화된 최종 가중치들은 그 다음 프로세스인 Expert model 학습의 참조 정보로써 활용됩니다.
  • L2은 각각 변환된 그래프의 표현을 사용하여 Expert models의 분류기가 본래 그래프의 구성과 해당 클래스를 정확하게 예측하도록 최적화하는 Cross Entropy 기반의 예측 정확도 (좌측)항과, Expert model들이 표현 사이의 거리 함수 (Frobenius norm)의 패널티 강도를 하이퍼파라미터로 조절함으로써 공통된 표현 공간으로 정렬되도록 강제하는 (우측)항의 합으로 구성되어 있습니다.

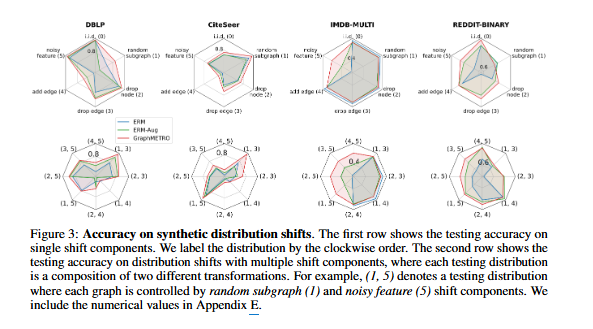
• GraphMETRO는 GOOD 실세계 벤치마크 데이터셋 및 합성 데이터셋에서 기존 방법들 대비 좋은 성능을 보였습니다. Fig 3의 합성 데이터셋 실험에서의 각종 성능 지표를 통해, 전반적으로 GraphMETRO (빨간색 선)는 대부분의 단일 및 다중 분포 변화 환경에서 ERM(파란색 선) 및 ERM-Aug(초록색 선)보다 높은 정확도를 보여주거나 최소한 동등한 성능을 유지합니다. 이는 GraphMETRO가 다양한 유형의 복잡한 분포 변화에 대해 더 강력한 일반화 능력을 가지고 있음을 시사합니다.
• 또한 Invariance matrix 분석 (Fig 4)을 통해 각 expert model이 해당 이동 요소에 대해 불변 표현을 효과적으로 생성함을 확인했으며, gating model은 실제 데이터셋에서 혼합된 분포 변화를 성공적으로 식별하여 성능 향상의 기저를 형성함을 보입니다.

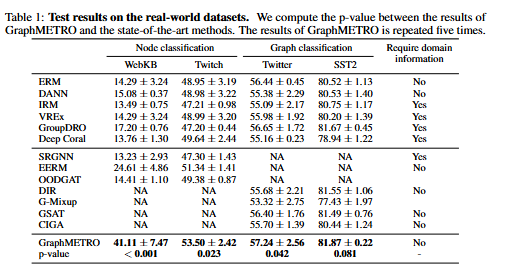
• 특히 WebKB에서 67%, Twitch에서 4.2%의 성능 향상을 보이며 실제 복잡한 분포 변화에 대한 우수한 일반화 능력을 입증했습니다. 주로 그래프 분류 작업을 위한 목적성을 갖고 있지만, 노드 분류 작업에도 쉽게 적용할 수 있습니다. 또한 데이터셋 내의 분포 변화 유형에 대한 해석과 통찰력을 제공할 수 있다는 장점 및 변화 요소들에 대한 불변성을 Theorem 1,2로부터 이론적으로도 보장됨을 언급합니다.
• 종합적으로 제안하는 GraphMETRO는 이질적인 그래프 분포 변화를 비공식적 가정을 통해 이동 요소들 분해하고 이들의 혼합을 정확하게 인지하는 Gating model, 각 요소들에 대응되는 Expert model의 일관된 표현 공간으로 정렬하는 계층적 프로세스들을 통해 실제 복잡한 분포 변화를 나타내는 다양한 케이스 실험에서 우수한 일반화 능력을 입증한 강력한 GNN 프레임워크를 제안합니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn