Social network analysis of Japanese manga: similarities to real-world social networks and trends over decades

[https://arxiv.org/pdf/2303.07208.pdf]

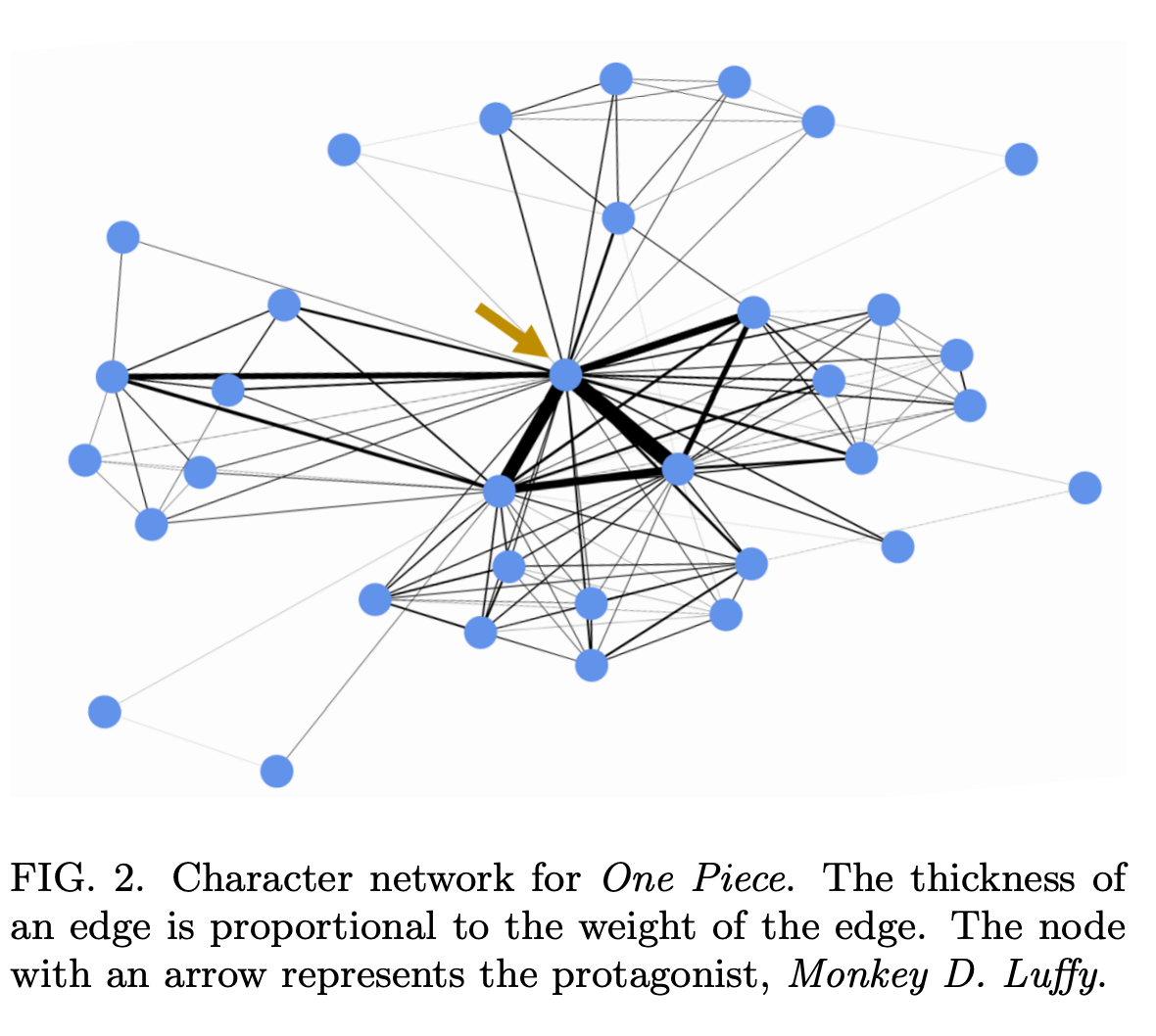
• 여러분들은 그래프 데이터가 언제 와닿나요? 주변에 있는 사물 혹은 인간 관계등이 직관적으로 표현될 때가 가장 이해하기도 쉽고 재밌었던것 같네요. 데이터 도메인에 대해 무의식적으로 이해하고 있기에 그렇지 않을까 싶습니다. 저는 ‘왕좌의 게임’ 미국 드라마에서 캐릭터들간의 관계들을 표현했던 그래프가 그 케이스를 잘 대표한다 생각합니다. 시나리오가 방대하다보니 드라마의 개연성을 높이기 위해 다양한 역할을 가진 인물들이 등장하다보니 일일이 다 기억하기가 힘들었었네요 :) 그 힘듦이 비단 저뿐만아니라 드라마 보신 다른분들도 공감하고 계셨나봐요. 마침 네트워크 과학을 하신분께서 드라마 인물간의 관계도를 지식그래프로 표현했던 케이스가 떠오르네요.
• 서두에 왕좌의 게임을 빗대어 드라마의 인물 관계도를 그래프로 표현한 케이스를 말씀드린 이유는 본 논문도 그와 흡사한 맥락을 띄고 있기 때문이에요. 바로, 일본 만화에서 등장인물간의 관계를 그래프로 표현한건데요! 이전에는 단순하게 관계를 시각적으로 표현하고 간단한 네트워크 분석을 진행했다면 본 논문에서는 조금 더 심오하게 접근합니다. 다음 두 가지 가설을 기반으로 접근을 하는데요. 1. 70년간 등장한 만화 캐릭터들을 분석해서 지금과 그때의 트렌드는 시스템적으로 다를것이며, 2. 이 분포들은 real-social network와 비슷할 것이다. 듣기만 해도 궁금하시지 않으시나요?!
• 결과부터 말씀드리자면, 인간의 소셜 네트워크와 유사하게 만화의 등장인물들도 다양한 연결 관계 가지고 있다고 합니다. 다양한 페이지에 불균형적으로 자주 나타나는 소수의 등장인물들이 등장함으로써 네트워크를 이끌어 간다고 하네요. 이를, 네트워크 정량화 지표 strength , average degree , bipartite → one-mode network and analysis , assortativity 등을 활용하여 그 결과들을 해석해봅니다.
• 이 중, 주방장에게 굉장히 흥미롭게 다가왔던 것은 SI 모델을 활용해서 Inter-Event Time (IET) distribution 을 분석하는 섹션이였습다. IET distribution 에서 heavy,tailed 에 속해있는 소수의 등장인물들이 해당 세계에서 어떤 영향을 미치는가에 대해 해석하는 부분이 너무 재밌었습니다.
• 현실 세계와도 비슷하다 라고 느낄수 있을만큼 설득력있게 글을 잘 전개해놓았으며, 방법론을 어떤식으로 접근했는지에 대한 기술에 대해 논리적으로 잘 기술해놓았어서 향후 아이디에이션에 많이 도움이 될 거 같다라는 생각이 들었습니다.
• 접근 방법론을 벤치마크하여 현업에서 HR하시는 분들이 적용해보시면 재밌는 결과가 나오지 않을까 싶네요…! 인사를 관리하는 입장이신 분들에겐 성과 측정을 정량화 한다는 점에서 매우 유용할거라 생각되지만, 관리 당하는 입장에서는 다른 관점이 있겠다 생각되어 이 또한 양날의 검이 되지 않을까 싶습니다 🙂

PyG 2.3.0

[https://github.com/pyg-team/pytorch_geometric/releases/tag/2.3.0]

• PyG 2.3.0 업데이트가 되었습니다! torch 2.0 개편 (torch compile) 됨에 따라, 역시 발 빠르게 업데이트했네요 ! 이전 pyg-lib 와 torch.compile 등을 조합하면 얼마만큼 성능이 향상될지 너무 기대되네요. 주요 업데이트 사항은 다음과 같습니다.
• PyTorch 2.0 Support
• Infrastructure Changes - there are now optional module torch (scatter , sparse, cluster , spline-conv) you just select one among them according to your task.
• Native PyTorch Sparse Tensor Support - now we use the flexible function to torch native tensor handling (sparse.tesnor).
• Explainability Framework - heterogeneous graph explanation & explainability metrics ease use support & ease to utilize visualization function.
• Accelerations - Nvidia(gpu),intel(cpu) accerlation.

Compiled Graph Neural Networks

https://pytorch-geometric.readthedocs.io/en/latest/tutorial/compile.html

Speedup mainly comes from reducing Python overhead and GPU read/writes, and so the observed speedup may vary on factors such as model architecture and batch size. For example, if a model’s architecture is simple and the amount of data is large, then the bottleneck would be GPU compute and the observed speedup may be less significant. - torch official document in ‘torch.compile() function description’

• compile 의 기능을 쉽게 말씀드리자면 torch code 를 jittable 하게 해줌에 있다고 보시면 되겠습니다. jit 이란 just-in-time 의 약자로써, 이 기능을 활용한다면 interprete → compile로 변환해줌으로써 좀 더 기계가 읽기 쉽게 코드를 번역해준다고 생각하시면 되겠습니다. 당연히 코드와 기계간의 상호작용에 걸리는 시간이 적어짐으로써 속도 또한 빨라지겠죠??
• torch geometric 에서도 compile tutorial 을 pyg 공식 도큐에 작성해놓았습니다. 다만 유의하실 점은 message passing aggregation and update에서 활용되는 torch scatter , sparse 그리고 pyg_lib는 아직 compile()에 optimization 이 되어있지 않기에, 업데이트와는 무관하다고 합니다.
• **torch.compile()**works fantastically well for many PyG models. Overall, we observe runtime improvements of nearly up to 300%.
• 무려 300배 가까이 성능 개선을 이뤄냈다고 합니다. 개선폭이 상당히 큰데요. 그만큼 적용이 어려울거라 생각하신 분들도 계시겠지만 , 단 한문장 model = torch_geometric.compile(model) 로 이 성능 개선을 경험해보실 수 있습니다.

ReFresh: Reducing Memory Access from Exploiting Stable Historical Embeddings for Graph Neural Network Training

[https://arxiv.org/pdf/2301.07482.pdf]

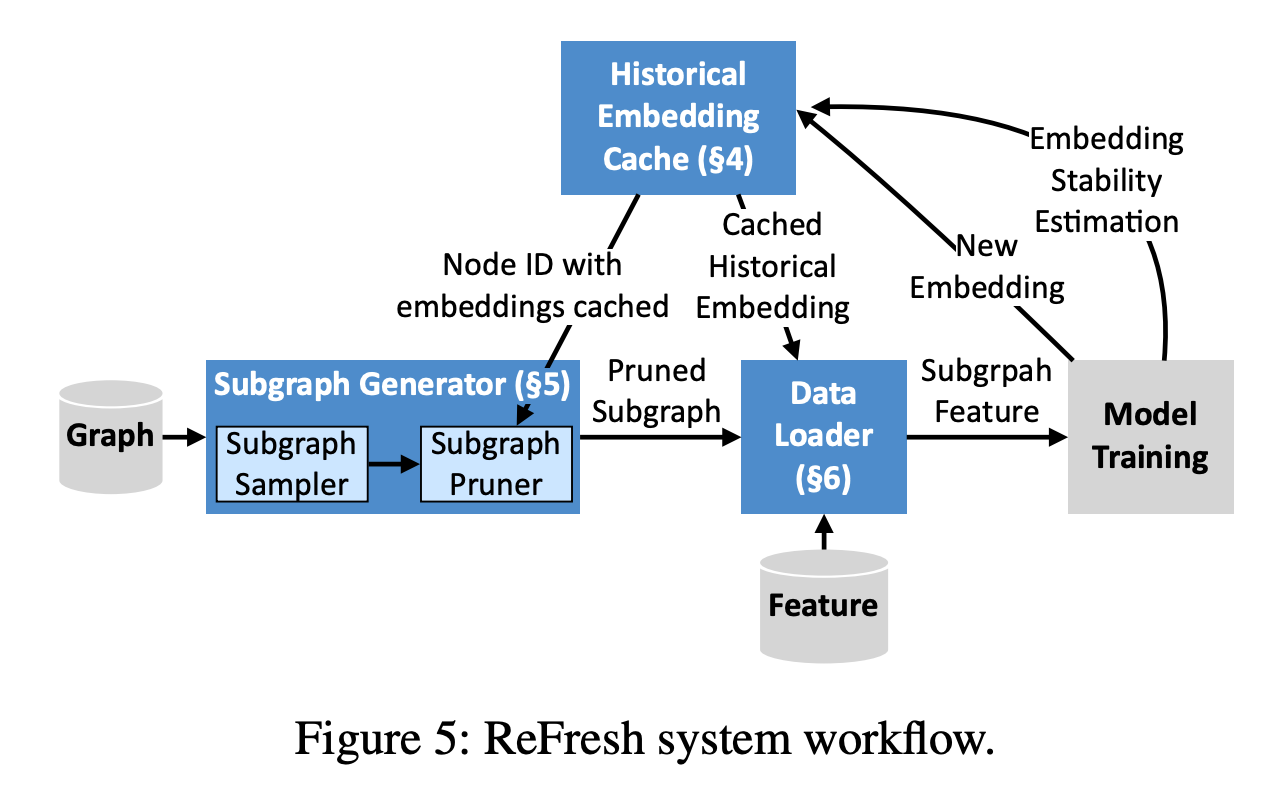
• GNN 에서 cost 가 많이 발생하는 여러 요소들 중 하나인 mini-batching 을 개선하고자 embedding 마다 tagging(cache)을 활용해서 cost를 줄이고자 시도한 논문입니다. layer 가 많아짐에 따라 hop of hops manner 또한 증가하며 message passing 으로 전달되는 정보량 또한 증감되는데 이 증감되는 정보량이 다들 제각각이기에, 특정시기에는 정보량 graident 가 대폭 상승되는 반면에 감소되는 측면도 존재합니다.
• 그렇다면 결국 이 정보를 저장하고 처리하는 부분인 GPU memory 에서 동적으로 이 모두를 분석하고 저장하는게 핵심이라 볼 수 있습니다. 이 부분을 동적으로 처리하기 위해 feature(graident) 마다 Stateness 와 Graident-based criteria 두 지표들을 활용하여 feature 를 reusing 할지 안할지를 고민하여 최적화 합니다.
• 이 최적화 , 모델 아키텍쳐의 핵심은 다음 3가지로 나뉘어집니다. 1. the historical embedding cache - graident 마다 cache marking 을 해주고 그 marking 들을 관리하는 policy build 모듈 2. the subgraph generator - policy 를 통해 선별된 subgraph 들을 잘 가져오기 위한 모듈. 3. the data loader - 선정된 subgraph 로부터 feature ,node 들을 fetching 해주는 모듈.  이 3가지가 유연하게 작동하며 최적의 임베딩 값을 도출해냅니다.
• model mini-batching 아키텍쳐를 통해 SOTA 와 비슷하게 정확도 성능은 가져가면서 속도는 최소 4.6 times  ~ 23.6 times faster before. 가 핵심 결과라고 보시면 되겠습니다. 유의깊게 보시면 좋을 부분은 cache marking 으로 오히려 additional burden 이 발생하는데 이를 해결하기 위해 COO,CSR → CSR2  pruning technique 을 활용하는 부분입니다. 이 부분은 참고로 torch.sparse 과 많이 연관되어 있기에, 한 번 익혀두시면 굉장히 좋을거라 생각되네요!
• difficulty in training large-scale GNN , motivation 부터 어떻게 해결할것인가에 대해 논리 전개가 잘 되어 있는 논문입니다. 개인적으로 가장 큰 문제점 이라 생각했던 부분인 ‘bottleneck of GNN’에 대해 설명부터 왜 이게 문제가 되는지에 대해 잘 작성되어 있다고 판단하여 더욱 유심히 보았네요.
• 저자 라인업을 보시면 아시겠지만 , mit amazon 등 산학연이 합동으로 연구한 결과이기에 연구적인 측면에서 이상과 현업에서의 현실이 적절하게 밸런싱되어 있는 논문이라 생각되어 더욱 신빙성을 더했다고 생각되었던 논문이네요. 한 번 통독해보시는것을 강력 추천드립니다!

Finally, a Fast Algorithm for Shortest Paths on Negative Graphs

[https://www.quantamagazine.org/finally-a-fast-algorithm-for-shortest-paths-on-negative-graphs-20230118]

• 그래프 입문할 때 마주하게 되는 유래 중 하나죠. ‘Seven Bridges of Königsberg’ 임의의 지점에서 출발하여 일곱 개의 다리를 한 번씩만 건너서 원래 위치로 돌아오는 방법을 찾기위해 그래프 이론을 접목했죠. 요즘 세대들에게는 ‘한 붓 그리기’라는 명칭이 더 와닿을거라 생각됩니다. 이 이야기를 꺼내게 되는 이유는 바로 그 맥락과 비슷한 shortest-path 에 대해 하기 위함인데요.
• 현재 graph 가 가장 잘 활용되는 분야 중 하나가 바로 navigation 분야라고 할 수 있습니다. 출발 지점과 도착 지점 사이의 최적거리를 찾는게 바로 shortest path of graph theory 문제로도 바라 볼 수 있기 때문이죠. 이 때 지점 사이에 위치하는 edge 를 도로라고 바라보고 그 도로의 특성에 따라 weight 를 지정해줍니다. 교통 상황에 따라 양수의 숫자를 기입하여 반영해주며 최적 동선을 유추하곤 하죠.
• 하지만 shortest path 에서 edge 에 양수 이외에 ‘음수’가 존재하는 상황도 있기 마련입니다. (양의 가중치로 표시되는) 가스 및 통행료 비용과 (음의 가중치로 표시되는) 운송 패키지 수입 간의 균형을 맞춰야 하는 배달 운전자를 생각해본다면 양과 음에 대해 모두 고려해야 하는 상황이 존재하는데 기존 shortest-path 알고리즘(다익스트라, greedy)와 같은 경우는 이 상황을 반영하기에 한계점이 있었습니다.
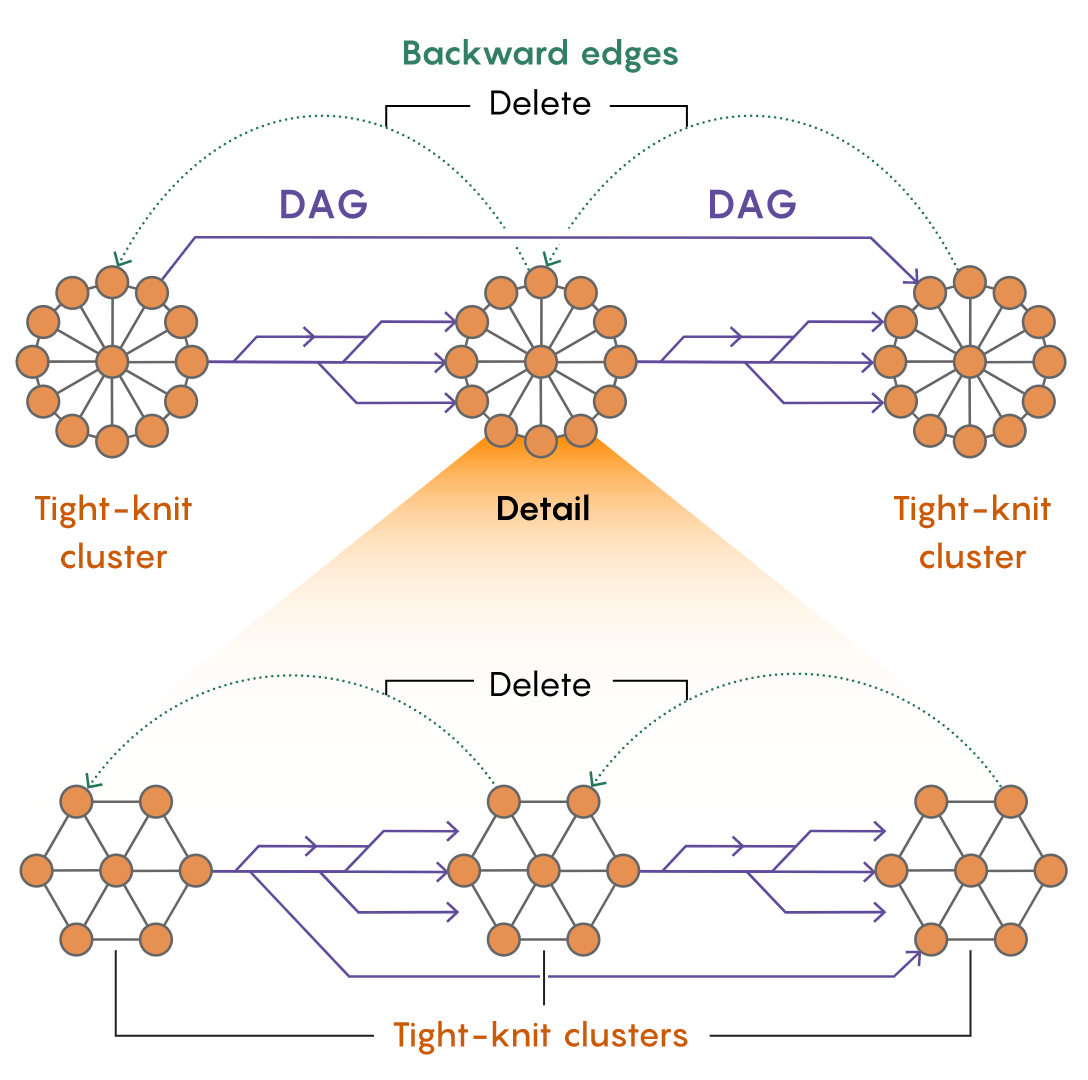
• 그 한계점을 극복하기 위해 그들은 저밀도 분해(tightly-connected) 와 유사한 방향 그래프에 대한 프랙처링 절차를 개발했습니다. 이 절차는 임의의 방향 그래프를 임의의 공정을 사용하여 소수의 가장자리만 삭제함으로써 일련의 촘촘한 클러스터로 잘라냅니다.
• 그 후, 그 클러스터들은 모든 가장자리가 같은 방향을 가리키는 희소 네트워크에 의해 연결됩니다. 최종적으로 DAG(directed acyclic graph)이 만들어집니다. 이 DAG 을 eliminated , deleted 를 iterative process 진행하며 negative weighted in shortest path 를 풀어나갑니다.