24년 8월 2주차 그래프 오마카세

Graph-based Semi-Supervised & Active Learning for Edge Flows

paper link : https://arxiv.org/abs/1905.07451

official code(Julia) : https://github.com/000Justin000/ssl_edge

배지훈

• 안녕하세요 독자 여러분들 ! 무더운 날씨에서도 건강하게 지내시고 계신가요 ? 최근 저도 방학을 맞이해서 귀국을 했는데, 말로만 들어서 와닿지 않았던 무더위가 바로 체감되더라구요. 건강이 우선입니다 !
• 저번 주까지 해서 토폴로지 신호 처리 (TSP) 관점에서 여러가지 개념들 및 적용 사례들을 전달해드렸습니다. 최대한 독자 분들의 이해를 돕기 위한 부가 설명들을 좀 많이 붙였더니 전체적인 글 복잡도가 높아진 것 같은 생각이 들긴 했습니다만, TSP에서 필수적인 요소들만 눌러 담았기 때문에 자세하게는 아니더라도 직관적으로 받아들여주셔도 무방할 것 같습니다.
• 이번에 전달해드릴 내용은 위의 TSP 개념을 바탕으로 Graph-based SSL 학습을 제안한 첫 논문으로, 기존의 노드 레이블이 기준이 아닌 엣지 흐름 상에서 SSL을 정의한 재밌는 논문을 가지고 왔습니다. 이전 오마카세 글 내용을 쉽게 연결지어 그래프 반지도 학습 사례에 완벽하게 적용한 내용들이 설명되어 있어서 부담없이 접근해볼 수 있을 것 같아 선정하게 되었습니다.
• 이번 글에서는 이전에 상기해보았던 기존 개념들을 생략하겠습니다. 혹시 이해가 안되거나 잊어버린 개념들이 있으시다면 해당 논문, 혹은 이전 글 내용을 참고해주시기 바랍니다.

Graph-based Semi-supervised Learning for Edge flows

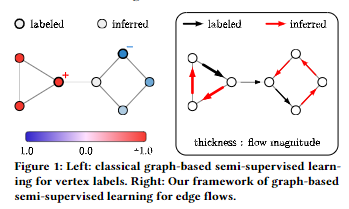
• Graph SSL (그래프 반지도 학습)은 레이블링 된 소수의 노드들을 기반으로 해당 데이터 샘플 상의 내재적 구조정보에 유사도 제약 (similarity or smoothness constraint)이 있음을 가정하여 주변의 비레이블링 노드 레이블을 예측하는 도메인으로 생각해볼 수 있습니다.
• 그래프 구조정보와 인접 노드 간 유사도 관계가 중요한 도메인인 만큼해당 그래프 데이터를 표현하는 연결 관계, 즉 엣지에 관련한 정보를 고려하는 것이 중요할 수 있습니다.
  • Fig 1와 같이, 기존 그래프 반지도 방법들은 노드 각각에 집중하여 인접 노드들에 최대한 동일한 레이블 정보를 할당하는 알고리즘 학습이 진행됩니다.
  • 하지만 엣지를 통해 한 노드로부터 다른 노드로 흘러가는 정보의 흐름, 즉 엣지 흐름 (Edge flow)을 고려하는 경우는 매우 드물며 이와 관련한 알고리즘 구축도 잘 되어있지 않습니다.
  • 대부분의 complex network (E.g. flow of energy, transportation network etc..)에서는 그래프 상의 엣지를 고려하는 것이 중요하다고 말씀드렸었습니다. 하지만 거대 그래프 (Large graph)의 경우 일반적으로 엣지의 개수는 노드 개수보다 무수히 많기 때문에 이를 Supervised learning 방법으로 접근하는 것은 한계가 있을 것입니다.
• 따라서, 저자들은 불변 토폴로지를 가지는 네트워크 상의 엣지 흐름을 SSL 방법으로 학습하는 방법을 제안합니다. 하지만 기존 노드 기반 SSL에서의 제약 조건인 smoothness를 그대로 엣지 흐름 상에 적용하는 것은 Sub-optimal results를 얻어낸다는 사실을 발견합니다.
  • 다음의 이유로, 엣지 흐름을 표현하기 위해 반드시 정의해야만 하는 방향성 (Orientation)의 존재를 언급합니다. 즉, 흘러가는 신호의 방향이 해당 네트워크 상에 정의된 방향성과 동일 유무에 따라 부여되는 부호가 서로 다를 수 있기 때문에, 이러한 관점에서 직접적인 적용이 어렵다는 것입니다.
  • 기존의 경우, 이러한 부호 정보를 고려하지 않기 때문에 엣지 흐름에 대한 새로운 알고리즘 정의가 필요하게 되었습니다.
• 이전 오마카세에서 전달해드렸던 것 처럼, 저자들은 새로운 알고리즘 정의를 위해 Divergence-free 혹은 Conserved한 엣지 흐름 정보를 기반한 제약적인 접근을 수행합니다.
  • Divergence-free / Conserved flow : 한 노드로 들어가는 정보의 총 흐름량은 그 노드로부터 빠져나가는 정보의 총 흐름량과 동일하다. 즉 흐름 과정에서 어떠한 손실이 없다.
  • 엣지 흐름에서의 Divergence는 edge Laplacian matrix (L_e = B^TB)으로부터 인코딩 되며, 다음 행렬을 중심으로 최적화 문제에 대한 Linear least-squares 문제를 정의하고 그에 대한 해를 구할 수 있을 때 완벽하게 보존 조건을 만족할 수 있으며, 다음 error에 대한 upper bound (최대 경계조건)을 파생할 수 있음을 언급합니다.
• 위에 대한 자세한 설명은 Methodology에서 설명드릴 수 있도록 하겠습니다.
• 또한 저자들은 비레이블 엣지 흐름의 정확한 추론을 위한 가장 유용한 레이블 엣지의 일부분을 선택할 수 있도록 하는 2가지 학습 알고리즘을 제안합니다. 다음을 Active semi-supervised learning으로 명칭하며, 무작위로 엣지를 선택하는 경우보다 훨씬 더 좋은 성능을 보장할 수 있었음을 증명합니다.

Methodology

• For vertex labels에 대한 설명은 여기서 생략하도록 하겠습니다. 참고를 위해 해당 논문을 확인해주시기 바랍니다.
• 위에서 가정한 Orientation & Convervation for Edge flows 조건을 활용하기 위해, 저자들은 각 노드들에 대한 divergence (한 노드로부터 들어오고 나가는 정보 흐름의 차이) 정보를 고려합니다.

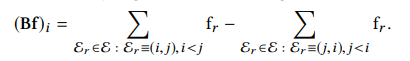
• 노드 인덱스 i에 대하여, 전자의 term은 해당 노드에서 빠져나가는 outflow 정보를, 후자의 term은 해당 노드로 들어오는 inflow의 정보를 나타내고 있습니다. 여기에서 B는 incidence matrix (포함 행렬)을 의미합니다.
• 두 flow 사이의 Smoothness를 정의하기 위하여, 다음 Divergence를 minimization하는 cost function을 아래와 같이 edge Laplacian (L_e)의 quadratic form로써 정의합니다.

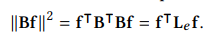
• 다음은 노드 기반의 smoothness를 정의하기 위한 graph Laplacian (L = D-A)의 quadratic form 형태와 유사한 듯 보입니다.
• 하지만, 이것을 직접적으로 사용하는 것은 위의 cost function = 0으로 만들어주는 유일한 해가 존재하지 않을 수 있는 문제가 야기될 수 있습니다. 따라서 유일한 해를 보장할 수 있는 추가적인 정규화 요소가 필요합니다.

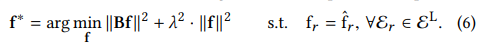
Spectral Graph Theory Interpretations

• 그래프 신호 처리 (GSP) 관점에서 노드 레이블 기반의 기존 방법들은 graph Laplacian의 고유분해(eigen-decomposition)를 통한 고유벡터 및 고유값을 바탕으로 각 노드별 신호 주파수를 활용합니다.
• 엣지 흐름의 관점에서 스펙트럼 분석을 진행하기 위해서는 포함 행렬 B의 특이값 분해 (Singular Value Decompositiono, SVD)를 통한 2가지 특이벡터 (Left/Right singular vectors)를 기반으로 접근해야 합니다.
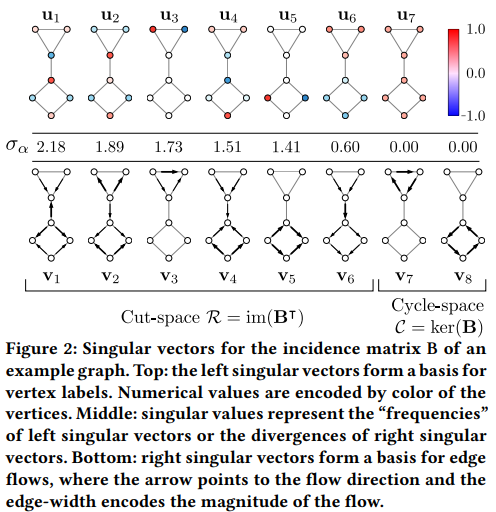
  • Left singular vector (u in figure 2) : Fig 2에서도 잘 표현되어 있듯이 노드 레이블에 대한 직교기저 벡터 (U)를 형성합니다. 즉, vertex-based SSL problem과 깊은 관련이 있습니다.
  • Right singular vector (v in figure 2) : 엣지 흐름에 대한 직교기저 벡터 (V)를 형성하며, 즉 edge-based SSL problem과 깊은 관련이 있습니다. 우리가 고려하고자 하는 divergence-minimization은 해당 벡터와 연관이 있습니다.
• 한마디로, 포함 행렬의 특이값 분해를 통해 우리는 한번에 node- & edge-based SSL problem을 연관지어 생각해볼 수 있게 됩니다.
• 2가지 특이 벡터를 기반으로 위의 정규화 요소가 포함된 최적화 문제를 아래와 같이 바꾸어 접근해볼 수 있습니다.

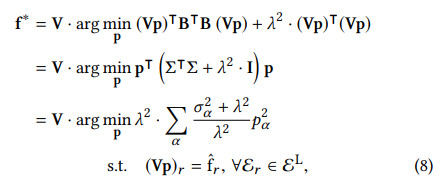
여기에서 p = V^Tf 표기는 Right singular vector (V)를 통해 스펙트럼 공간으로 맵핑되는 엣지 흐름 신호 (f)의 스펙트럼 계수를 나타냅니다.

• 식 8의 전개 과정을 하나씩 이해해보기 보다는, 결과적으로 마지막 식을 최소화하는 스펙트럼 계수 p를 찾는 것이 중요하며, 이말인 즉슨 최적의 right singular vector V를 찾아내는 것이 목적이 된다는 정도만 알고 넘어가셔도 될 것 같습니다.
• 위에서도 언급하였듯이, V는 직교기저 벡터로써 엣지 흐름을 표현하는 스펙트럼 공간 (\R^{m})의 기저 벡터가 됩니다. 다음 공간을 분해해서 독립적으로 엣지 흐름의 신호 특성을 세밀하게 분석하기 위해서 다음의 2가지 직교 하위공간 (: Cut- & Cycle-space in Fig 2)을 생각해봅시다.

Signal smoothness, cut-space, and cycle space

• 엣지 흐름이 표현되는 공간을 직교 기저 V를 통해 2가지 하위공간으로 나누어서 독립적인 흐름의 신호를 분석할 수 있게 되었습니다.
• 첫번째 하위 공간은 cut-space R= im(B^T)로 정의되며, 0이 아닌 특이값에 대응되는 특이벡터 V_R로부터 스팬됩니다. 해당 공간에서의 임의의 벡터는 B^Ty꼴로 표현되기 때문에 Gradient space라고도 불립니다. 다음은 호지 분해 (Hodge decomposition)를 통해 분해되는 공간의 형태와 유사합니다.
  • Grad-space는 두 노드 사이의 potential scalar value 차이로부터 유도되는 gradient flow를 표현하는 공간으로써 Non-cyclic space임을 이전 게시글에서 설명드렸습니다.
• 두번째 하위 공간은 cycle-space C = ker(B)로 정의되며, 0의 특이값에 대응되는 특이벡터 V_c로부터 스팬됩니다. 이름 그대로, 다음 공간은 흐름의 circulation을 나타내는 벡터 f와 연관이 깊으며, 포함 행렬 B에 대한 kernel space이기 때문에 위에서의 Divergence-minimization cost function (L_e의 quadratic form)의 해가 됩니다. 또한 다음은 호지 분해로부터 얻어지는 Harmonic space의 형태와 유사합니다.
  • 다음 공간에서 얻을 수 있는 놀라운 정보는, 0의 특이값에 대응되는 특이 벡터의 개수 c는 연결 그래프(connected graph) 상의 엣지 개수 (m) - 노드 개수 (n) + 1 (c = m - n + 1) 와 같으며, 이는 해당 그래프 상의 독립적인 사이클 (cycle) 개수와 일치함을 알 수 있습니다.
• 특이값은 Left / Right singular vector에 대한 "frequency"를 표현하고 있기에 이것으로부터 엣지 흐름에 대한 "Smoothness"를 쉽게 정의해볼 수 있겠습니다.
  • Fig 2에서도 잘 나타나있듯이, 특이값 = 0에 해당하는 2가지 특이 벡터 v_7, v_8의 경우 해당 그래프의 cyclic한 엣지 흐름을 보여주고 있으며, 나머지 벡터들의 경우 0이 아닌 Divergence flow를 갖는 엣지 흐름을 보여주고 있습니다.
• 저자들은 Right singular vector로부터 얻어지는 Divergence-free (혹은 Cyclic space)의 엣지 흐름 공간에서 엣지 흐름 신호에 대한 보존 조건을 완벽하게 파생할 수 있음을 보여주고 있습니다. 다음 사실만 짚고 넘어가셔도 무방할 것 같아 이와 관련한 자세한 설명은 생략하도록 하겠습니다. 혹시 자세한 증명이 궁금하신 독자분들께서는 해당 논문의 세션 2.3을 참고해주시기 바랍니다.

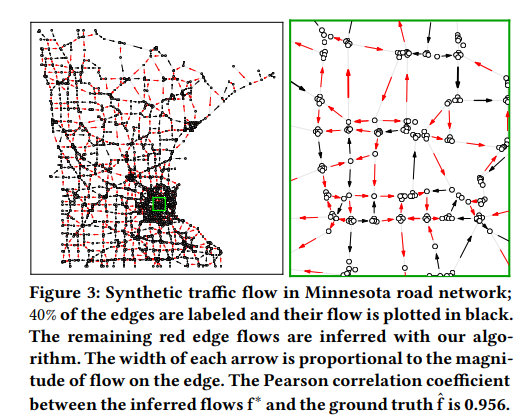
• 위의 Divergence-free space에서 cyclic한 엣지 신호를 바탕으로 Fig 3의 Synthetic dataset 상에서 빨간색 신호를 추론한 결과, 실제 엣지 흐름과의 피어슨 상관계수 (Pearson correlation) 값이 0.956라는 높은 정확도의 결과를 얻어낼 수 있었다고 합니다.
  • Fig 3의 오른쪽 그림와 같이, 검은색 레이블 신호를 바탕으로 빨간색의 신호들이 cycle을 형성하면서 추론된 결과를 쉽게 확인해볼 수 있었으며, 이전 게시글에서 언급해드렸던 엣지 신호의 Harmonic components이 SSL 문제에서 중요한 역할을 수행할 수 있음을 확인해볼 수 있었습니다.
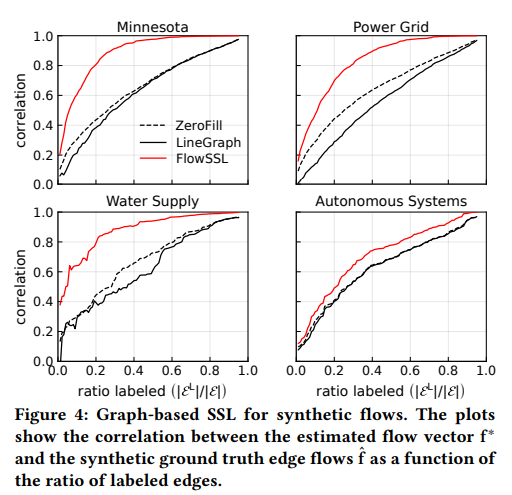
  • Fig 4에서도 기존의 다른 Graph SSL 방법보다 더 좋은 결과를 정량적으로 확인해볼 수 있습니다.

Active Semi-supervised Learning

• 비레이블링된 엣지 흐름을 찾아낼 수 있는 방법을 알았으니, 이제는 전체적인 엣지 흐름을 결정할 수 있는 가장 유익한 레이블 엣지들을 찾아내는 것에 관심을 가질 수 있을 것 같습니다.
• 이를 위해, 저자들은 Rank-revealing QR(RRQR), Recursive Bisection(RB) 이름의 2가지 Active learning algorithm을 제안하였습니다. Appendix에서 제공하는 코드의 순서에 따라 해당 알고리즘을 이해하는 것이 더욱 좋을 것 같습니다.
  • RRQR의 방법은 최소 특이값을 최대화하는 방식으로 레이블을 선택하는 방법이며, NP-hard의 문제를 해결하기 위해 QR decomposition을 활용하여 휴리스틱하게 rank를 매겨 선택하는 방식을 설계하였습니다.

• 먼저 cyclic한 엣지 흐름을 나타내는 cycle-space C = ker(B)에서 직교 기저벡터 V_c를 계산하고, 다음 벡터의 행 요소들에 대한 pivoted QR decomposition을 수행하여 가장 유용한 레이블 엣지 인덱스 정보를 얻어냅니다.
• RB의 방법은 네트워크 전체적인 흐름 패턴에서 글로벌 트렌드를 포착하도록 설계하였습니다. 자세한 내용은 아래의 Code snippet을 통해 알고리즘 동작을 이해하고 넘어가셔도 무방할 것으로 생각합니다.

• 마지막으로, 저자들은 Divergence-free (Cyclic) 관점 뿐만 아니라 Cyclc-free (Non-cyclic)의 경우도 고려하여, 기존의 호지 분해 개념을 활용하는 SSL 방법을 제안합니다.
  • 간략하게, 호지 분해를 통해 얻어지는 3가지 하위 공간 중, Curl-free condition ( ||C^Tf|| = 0 )을 통해 해당 네트워크의 모든 삼각형 (2-complex) faces 상의 엣지 흐름 합이 0이되는 경우에 초점을 맞춥니다.

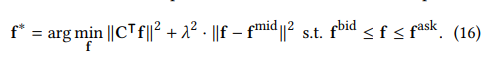
• 동일한 Constrained regularization term을 추가하여 모든 삼각형 면 상에서의 curl components를 최소화하는 최적화 문제의 해를 찾는 방향으로 접근하며, 'Fair pricing of foreign currency exchange rates'라는 금융 어플리케이션 문제를 해결하고자 하였습니다.

Summary

• 이번 주 오마카세는 그래프 상의 엣지 흐름 정보 기반 반지도 학습 방법을 제안한 논문을 소개해드렸습니다. 또한 비레이블 엣지 흐름의 예측 성능을 향상시킬 수 있는 그래프 상의 유용한 엣지들을 선택할 수 있는 2가지 Active learning algorithm도 같이 설계하여, 다양한 어플리케이션 상에서 기존 Graph-based SSL 방법보다 좋은 성능을 얻어낼 수 있음을 보여주었습니다.
• 다음 논문은 저번 주까지 전달해드렸던 오마카세의 2-simplex 상의 엣지 흐름 관련 TSP 개념을 1-simplex에 대응되는 그래프 데이터 상의 적용으로 단순화하여 상대적으로 쉽게 접근합니다.
• 그리고 비레이블 엣지 추론을 위해 노드 레이블 및 엣지 레이블을 한번에 활용하고자 SVD를 통한 2가지 직교 하위공간 상에서 표현되는 Divergence-free (혹은 Cyclic) 엣지 흐름 (Fig 2)을 수학적으로 모델링하여 적용합니다.
  • 실제로, Ground truth (혹은 해당 그래프 전체에서 Global-circulation하는) 엣지 흐름은 Cyclic-space 상에 존재하고 있기 때문에 Divergence-free한 엣지 흐름 및 그 공간 (위 글에서의 Ker(B), Fig 2 참고)을 고려하는 것은 적절한 분석 방법이 될 수 있습니다. 하지만, 해당 네트워크 상에 Circulation-flow가 존재하고 있다는 (본 논문에서의) 사전적인 가정을 만족해야 합니다.
  • 자세한 유도 과정을 다루진 않았지만, Divergence-minimizing의 Linear least-squares 문제에 대한 Unique Solution을 위해 추가적인 Regularization term이 필요하게 되었습니다.
• 전체적인 내용을 한번에 전달드리기엔 어려움이 있어서 일부 내용들은 생략하게 되었으나, 네트워크 상의 그래프 엣지를 통한 정보의 흐름을 분석하는 도메인에 관심이 있으신 독자분들은 꼭 한번쯤 해당 논문을 정독해보시는 것을 추천드리고 싶습니다 !
• 글을 마무리하기에 앞서, 그래프 오마카세를 함께 만들어나갈 마음이 있으신 분들을 구하고 있습니다. 그래프 주제로 글 연재하는 것에 관심이 있으신 분들께서는 언제든지 제 메일주소로 편하게 연락주시면 감사하겠습니다 !

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn