24년 8월 3주차 그래프 오마카세

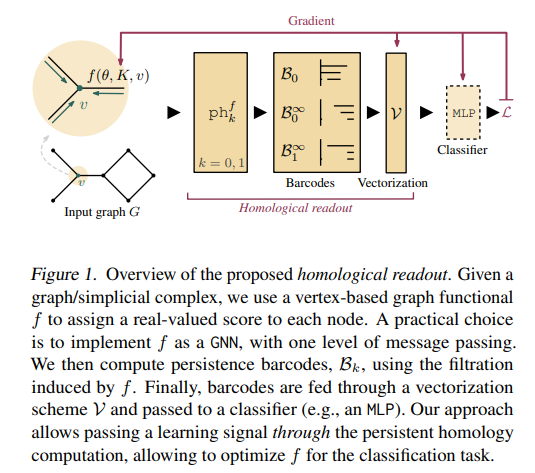
Graph Filtration Learning

paper link : https://arxiv.org/abs/1905.10996

official code : https://github.com/c-hofer/graph_filtration_learning

배지훈

• 안녕하세요. 이번 주 오마카세는 토폴로지 신호 처리 도메인에서 벗어나, 그래프 토폴로지를 학습하는 메커니즘에 대한 방법을 제안한 논문을 한개 가지고 왔습니다.
• 엣지 흐름의 정보에서 벗어나, 일반적으로 그래프 데이터에서 고려할 수 있는 노드 간 메세지 전달 과정에 토폴로지 정보를 포함시켜 한번에 학습할 수 있는 메서드로, 토폴로지 딥러닝 (TDL) 도메인 상에서 꽤 많은 주목을 받았던 논문이었어서 독자 여러분들께 한번 소개해드리고자 합니다.
• 그래프 분류 (Graph classification) 문제에서 집계된 노드 정보들을 글로벌한 그래프 차원에서 표현하고자 반드시 설계되어져야 하는 Readout 레이어에 초점을 맞추어, 어떻게 해당 그래프 데이터 상의 토폴로지 정보를 전체 그래프를 표현하는 데 효율적으로 활용할 수 있을까? 에 대한 질문 해답을 찾고자 하였습니다.
• 그에 대한 해답을, 본 논문의 저자들은 지속성 호몰로지 (Persistent homology) 개념을 도입함으로써 위의 Fig 1에서 나타내고 있는 새로운 그래프 필트레이션 학습 방법 (Graph Filtration Learning)을 제안하게 됩니다. 세부적인 내용은 아래의 Background (e.g. 호몰로지, 지속성 호몰로지, 지속성 바코드) 및 Methodology 부분에서 자세하게 다루어보도록 하겠습니다.
  • 주어진 그래프를 하나의 simplicial complex (정확하게 1-simplicial complex)로 고려하고, 지속성 호몰로지를 활용하여 시간에 따라 변화하는 그래프 상의 부분적 토폴로지 정보 (e.g. 연결 요소, 루프)를 추적하여 글로벌 구조정보를 포착하는 'Homological readout operation'을 제안합니다.
  • 다음은 데이터셋의 특성에 맞추어 사전 정의되어지는 permutation invariant한 readout layer (e.g. summation, graph-pooling)이 아닌, 학습 가능한 필터 함수를 사용한다는 점에서 그 의의가 있습니다.
• 지속성 호몰로지를 그래프 분류 문제에에 활용했던 사례는 기존에도 있었습니다. 하지만 학습 차원에서 활용되기 보다는 passive manner로서, 일종의 임베딩 함수 (f)로 활용됩니다. 즉, 지속성 호몰로지를 단순 특징 추출 단계로써만 활용하는 데 그치고 있습니다.
  • (구체적으로) 이는 전체적인 토폴로지 정보를 요약하는 Readout layer 단을 통과하기 전의 vectorization (벡터화) 프로세스 및 분류기에 제공되는 추출된 특징을 제한시켜 일반화 및 바이어스 학습의 문제를 야기할 수 있음 저자들은 언급합니다.

Background

• 제안 방법을 이해하기 위해 몇가지 알아두고 있어야 할 호몰로지 이론의 핵심 개념들이 있습니다. 지속성 호몰로지 (persistent homology), 필트레이션 (filtration), 지속성 바코드 (persistent barcode)에 대해 본 논문에서 잘 요약 설명해주고 있으니 이 부분에 대한 자세한 설명은 생략하고, 핵심 정의들만 간략하게 전달해드리고 넘어가겠습니다.
• 위키백과 및 여러 다른 블로그의 설명을 같이 링크로 걸어놓았으니, 직관적인 이해를 원하시는 독자분들께서는 추가적으로 참고 부탁드립니다.

1. 호몰로지 (Homology) : 한 대상(X)에 대한 정보를 포함하는 연속 그룹/모듈의 시퀀스에 대한 체인 컴플렉스 (Chain complex; Simplex들의 선형 결합 꼴로 나타나는 복합 컴플렉스 구조)를 나타내는 호몰로지 군(Homology groups)을 기반으로, X의 내재적 토폴로지 속성들을 연구하는 핵심 개념입니다.

• 아래의 식 1과 같이 바운더리 연산자 (Boundary operator)의 kernel space 및 image space에 대한 몫공간 (Quotient space)으로 정의됩니다.

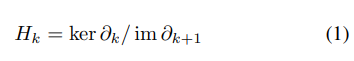
• 호몰로지 군의 랭크 (rank)를 베티 넘버 (Betti number)라고 하며, 다음 베티 넘버 값으로부터 연결 요소(Connected components) 혹은 루프 (loops)의 개수를 알 수 있습니다.
• 대표적 호몰로지 예시로서, 대수적 위상수학 (Algebraic topology)의 단체 호몰로지(Simplicial Homology)가 있습니다.

2. 필트레이션 (Filtration) : 대상 X의 시퀀스에 대한 부분 순서 집합 구조를 나타내는 개념입니다. 위의 Simplicial Homology를 고려할 때, 다음 필트레이션은 해당 Simplicial complex의 진화과정을 표현한 Sub-complex의 증가하는 배열 (ascending sequence)로 정의할 수 있습니다.

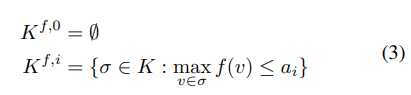
• 즉, 현재 컴플렉스가 어떻게 만들어졌는지 그 과정을 나타내는 것을 필트레이션이라고 합니다. 토폴로지 관점에서, 다음 필트레이션 과정으로부터 얻어지는 하위 구조들의 지속성(Persistence) 정보를 분석하는 것이 매우 중요합니다.
• 다음을 계산하는 대표적인 알고리즘으로 비에토리스-립스 필트레이션 (Vietoris-Rips Filtration)이 있습니다.

3. 지속성 호몰로지 (Persistent Homology) : 위의 필트레이션 과정이 제공하는 추가 정보들을 활용하여, 각 단계에서의 독립적인 호몰로지 군들 사이의 포함 관계정보를 연결시켜주는 개념입니다.

• 이름 그대로, 공집합으로부터 완전한 컴플렉스 까지의 모든 스케일 시간에 대하여, 특정 필트레이션 시간에서 해당 호몰로지 정보가 얼마나 지속되는지를 추적할 수 있게 해줍니다.

4. 지속성 바코드 (Persistent Barcode) : 위의 지속성 호몰로지를 측정하는 바코드 형태의 인코딩 정보를 multiset 형태로 나타냅니다.

• 주어진 Simplicial Complex (K)와 필터 함수 (f)에 대해서, k차 지속성 바코드 (B_k)는 K의 맵핑 함수로써 아래와 같이 정의할 수 있습니다.

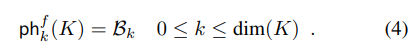
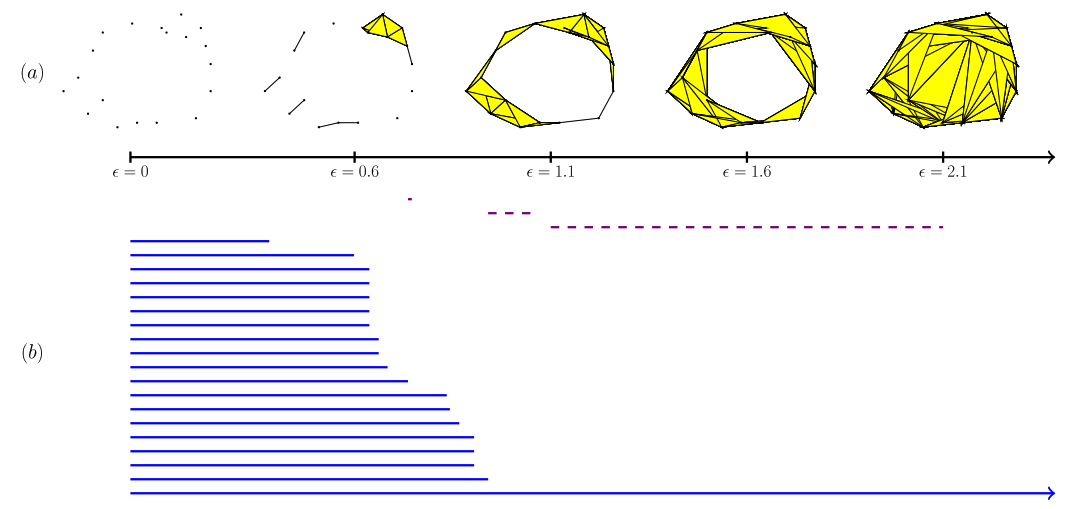
• Fig 1의 ph 기호가 무엇을 의미하는 지 알았습니다. 그리고 그래프는 1-simplex와 동일하기 때문에 k = 0, 1의 경우만 고려하면 됩니다.
• 위의 지속성 바코드 그림에서 제일 아랫부분의 파란 선은 무한 지속성(infinite persistence)을 나타내는 정보를 보여주고 있습니다. 다음은 그래프 전체에 글로벌하게 퍼져있는 정보임을 직관적으로 알 수 있습니다.
• 그래프 분류 문제에서, 해당 그래프의 성장 프로세스를 위의 필트레이션 혹은 지속성 개념의 정보를 가지고 생각해볼 수 있을 것 같습니다.
• 즉, 그래프 혹은 1-simplex 상의 호몰로지 정보의 변화를 추적하고, 다음을 0차, 1차 지속성 바코드 (B_0, B_1) 상에 나타내어 추가적인 그래프 상의 토폴로지 정보를 활용해보는 아이디어를 떠올릴 수 있습니다. 다음 아이디어가 바로 해당 논문에서의 모티베이션이라 보시면 되겠습니다.

Methodology : Filtration Learning

• 제안 방법은 사전 선택된 필터 함수를 사용하는 것 대신에, end-to-end 방식으로 학습할 수 있는 것에 초점을 맞춥니다. 저자들은 다음을 위해 지속성 호몰로지가 수행되면서 구해지는 Gradient를 역전파시키는 능력을 부여하는 것(참고 논문)이 중요하다고 강조합니다.
• 식 3의 필트레이션 정의로부터 고려해야 할 인자는 2가지 (K : given complex, f : filter function) 입니다.
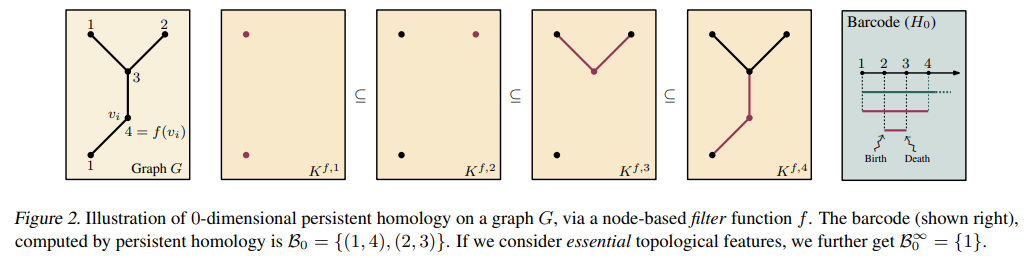
  • Fig 2와 같이 각 단계에서의 K는 discrete하게 변화하기 때문에, gradient-based optimization의 대상이 아니라는 것은 명백합니다.
  • 하지만, 학습 가능한 함수 f는 학습 파라미터를 가지고 있을 것이며, 다음 파라미터 값에 따라 필트레이션에서의 지속성 호몰로지 결과가 달라질 수 있습니다. 즉, 다음 함수는 학습 파라미터에서 반드시 미분 가능해야 하다는 조건을 만족해야 합니다. (Def. 1 참고)

• 학습 가능한 필터 함수 f는 주어진 simplex K의 각 노드 v에서 학습 파라미터 \theta에 미분 가능해야 합니다. 이러한 함수를 저자들은 학습 가능한 파라미터를 갖는 learnable vertex filter function라고 명칭합니다.
  • 실제로 위의 정의는 이론적 부분을 단순화하기 위해 오직 1가지 학습 파라미터를 갖는 경우를 고려한 것이며, 실제로는 n개의 학습 파라미터가 놓여있는 n차원 실수 공간 전체를 고려해야 합니다.
• 자연스럽게, 식 4로부터 학습 가능한 지속성 바코드 (Learnable persistent barcode) 역시 정의할 수 있습니다. 하지만 ph 함수로부터 인코딩되는 바코드 공간 (\B)은 각 바코드 결과가 서로 독립적이기 때문에 (A roadmap for the computation of persistent homology. 그림 참조), 추가 실수 공간으로의 맵핑 함수를 추가함으로써 다음 공간에서의 미분 가능성을 부여해주어야 합니다.
  • 다음을 Vectorization (벡터화, V) 프로세스라고 하며, 특정 조건 하 (Lemma 1 참고)에서 End-to-end의 학습 가능한 필터 함수를 설계하는 데 필수적인 '미분성(Differentiability)'이 보장되는 지속성 바코드 함수 ph를 아래와 같이 정의할 수 있습니다.
    • 다음은 포인트 클라우드 상에서 벡터화 방법을 정의하는 DeepSet과 유사합니다. 벡터화의 시초 격인 논문이기에 이것도 나중에 꼭 읽어보시는 것을 추천드립니다 !

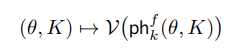
• 지속성 바코드에 대한 벡터화 방법들이 연구되어져 왔으며, 저자들은 이전 1저자 분께서 제안한 동일한 방법 (Rational hat structure)을 사용하였다고 합니다.

• 벡터화 함수 V는 지속성 바코드 공간의 독립적 바코드 (line)들을 연속적 실수 공간 상으로 맵핑해주는 함수가 되며 (line space -> real-value space), 그로부터 각 바코드 별로 부여되는 실수 공간 상의 좌표 (b,d)의 합산 스칼라 값을 얻을 수 있습니다.
  • 여기에서 b, d는 해당 바코드가 생겨나는 birth 및 소멸하는 death의 시간 t 값을 각각의 앞 이니셜을 따가지고 왔습니다. {= (t_b, t_d)} 그리고 2차원 좌표 실수 공간에서 스칼라 공간으로 맵핑하는 s는 위의 rational hat 함수를 사용하였습니다.

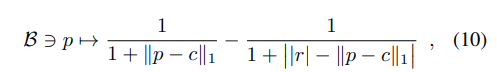
• c (center), r(radius)은 학습 가능한 파라미터이며, 직관적으로 다음 함수는 해당 바코드의 각 포인트 좌표 p = (b,d)에 대한 "Centrality"를 계산하는 것으로 이해해볼 수 있습니다.

Analysis of Lemma 1

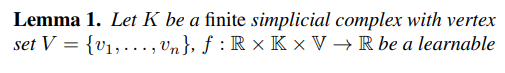
• Lemma 1의 조건 하에 미분성이 보장된 ph 함수는 해당 필트레이션 값이 pairwise distinct하다는 중요한 가정을 담고 있습니다. 다음 가정이 만족되지 않는다면, Simplicial complex의 독특한 incident property에 의해 sorting permutation을 uniquely defined 할 수 없게 됩니다. 그로부터 problematic scenario (아래 예시 참고)가 많이 발생될 수 있음을 저자들은 강조합니다.

Problematic scenario (Fig 3)

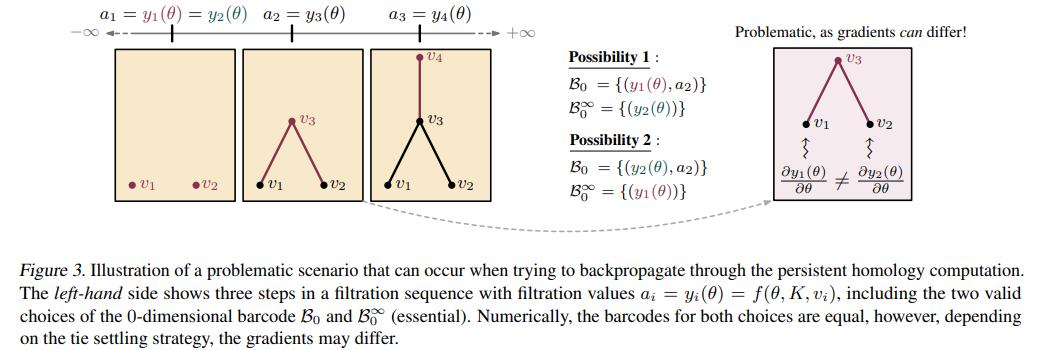
• 다음 문제에 대한 설명이 조금 복잡할 수 있는데, 한마디로 다음 문제는 필트레이션 과정에서 얻어진 동일한 지속성 바코드의 임베딩 스칼라 값이 Fig 3의 Possibility 1, 2와 같이 다른 포인트로부터 구해질 수 있게 되며, Gradient backpropagation 과정에서 잘못된 업데이트 결과를 야기할 수 있다는 것입니다.
  • 굳이 pairwise distinct하다는 제한 조건이 아니어도, 실제로 일반적인 Readout operator로 사용되는 maxpool에서도 종종 나타나는 문제적 현상입니다.
  • maxpool은 주어진 집합 내에서 최대값인 스칼라 (z)를 반환하는 함수로써 permutation invariant함을 보장할 수 있는 함수인데, 예를 들어서 해당 집합 내에 동일한 최대값 (y1 = y2 = z)이 존재한다고 하였을 때, 다음 gradient을 과연 y1에게 backpropagation 해야 하는지 y2에게 해야하는가? 의 관점에서 동일한 문제가 발생할 수 있다는 것입니다.
  • 다음 문제를 완화하기 위해, 저자들은 아래와 같이 tie-settling strategy을 활용하여 바코드 좌표 (a,b)를 평균 집계 방식으로 대체합니다.

• 다음 방법은 비록 학습 파라미터 개수 n이 클수록 연산적으로 매우 비싸지만, 실질적으로 독립적인 gradient를 형성하는 데 도움이 되었으며 해당 problematic scenario 완화에 자연스러운 선택이 될 수 있음을 저자들은 밝힙니다.
• 다음의 미분 가능성에 대한 요소도 고려해야 하지만, 이는 해당 논문에서 다루지는 않고 자세한 증명은 앞으로의 과제로써 남겨둔다고 합니다 !

Experiment

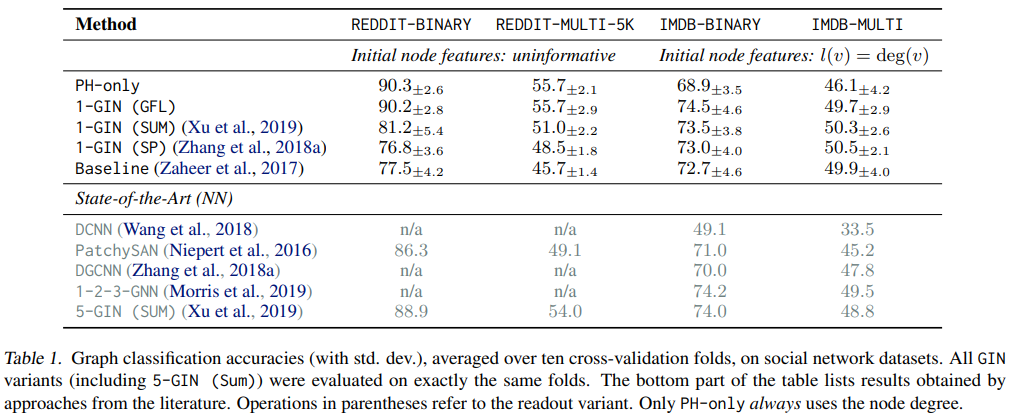
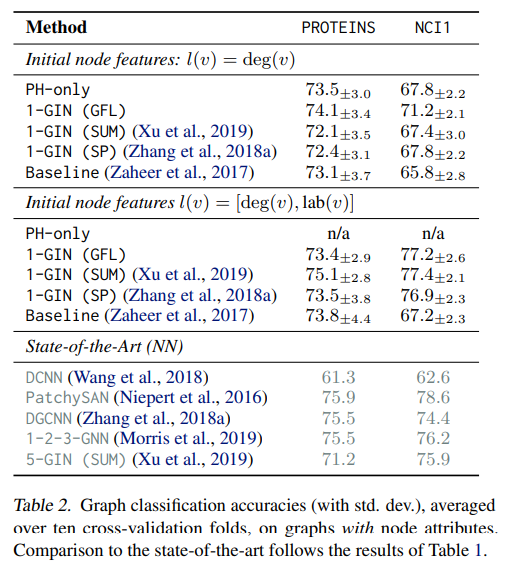
• 저자들은 필터 함수 f로써 1-GIN network를 활용하였으며, 기존의 단순 특징 추출자로써 지속성 호몰로지 (PH)를 사용한 경우와 Readout layer로써 SUM, SP (Sort pooling)을 사용한 경우, 그리고 벡터화의 시초인 DeepSets, 그리고 다양한 SOTA 모델들과 실험 비교를 진행하였습니다.
  • 실험 결과에 대한 자세한 설명 및 Complexity & Runtime 내용은 생략하겠습니다.

Summary

• 이번 주 오마카세는 그래프 분류 문제에서 필트레이션 기법을 활용하여 그래프 데이터의 발생 및 소멸 과정을 추적하고, 각 단계에서 추출한 토폴로지 정보들을 벡터화를 통해 Readout 레이어에 공급, 최종 분류 정확도 성능을 향상시킬 수 있음을 보인 논문을 리뷰해보았습니다.
• 메세지 전달 메커니즘으로 학습된 노드 간 pairwise relations을 반복적으로 집계하여 글로벌한 그래프 정보를 얻어내는 기존 방법을 학습 가능한 토폴로지 추적 과정과 지속성 바코드 활용이라는 새로운 접근법을 통해 데이터셋 특화된 Readout layer 선택의 한계에서 벗어날 수 있었습니다.
  • 저자들은 구체적으로 지속성 호몰로지 계산과 미분 가능한 벡터화 방식을 결합하여 학습된 Gradient를 Backpropagation하는 방법을 이론적으로 확립하였습니다.
  • 추가적으로 발생 가능한 Gradient backpropagation 모호성 문제를 tie-settling strategy로 완화시킴으로써 End-to-End한 GFL 방법을 제안할 수 있었습니다.
• DeepSets 논문을 필두로, 보통 포인트 클라우드 데이터 상에서 적용되었던 필트레이션 및 호몰로지 개념을 그래프로 확장하여, 글로벌 구조 정보를 추출하기 위한 그 발생 과정을 추적하여 각각의 토폴로지 정보를 집계하는 새로운 아이디어를 제공하였으며, 기존 GNN 모델 (본 논문에서는 1-GIN)과 효과적으로 결합할 수 있음을 보여준 것에 큰 의의가 있다고 생각합니다.
• 글을 마무리하기에 앞서, 그래프 오마카세를 함께 만들어나갈 마음이 있으신 분들을 구하고 있습니다. 매주 그래프 주제로 자유롭게 뉴스레터를 연재하는 것에 관심이 있으신 분들께서는 언제든지 제 메일주소로 편하게 연락주시면 감사하겠습니다 !

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn