24년 8월 4주차 그래프 오마카세

Simplicial Neural Networks

paper link : https://arxiv.org/abs/2010.03633

official code : https://github.com/stefaniaebli/simplicial_neural_networks

video : https://www.youtube.com/watch?v=2cidzWXH_vg&t=21s

배지훈

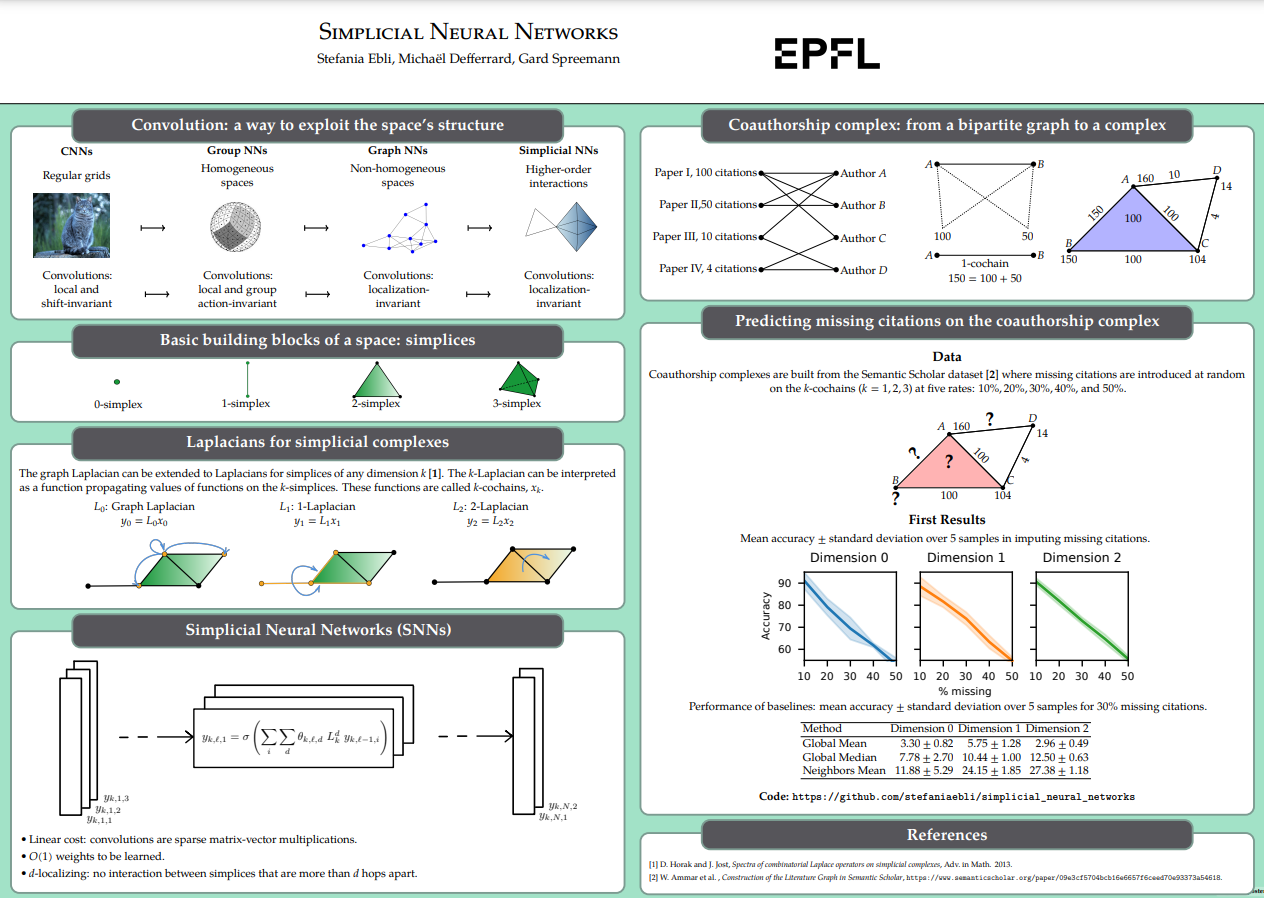
• 이번 주 오마카세에서는 Simplicial complex의 higher-order interactions을 컨볼루션 연산을 통해 학습할 수 있는 시초의 단순 신경망 모델을 제안하여 이후의 많은 관련 연구의 인용이 되고있는 'Simplicial Neural Networks' 논문을 전달해드리고자 합니다.
• Spectral graph convolution network로 유명한 Chebnet의 아버지 M. Defferrard이 연구에 참여하였음을 보아, 'Chebnet과 같은 스펙트럼 그래프 컨볼루션의 개념을 Simplical complex와 같은 higher-order complex상으로 어떻게 확장시켜 정의한 모델인가?' 라는 단순한 궁금증으로 논문을 읽어보았던 것 같습니다.
• 포스터 세션으로 제출된 논문이다 보니 해당 아이디어의 설명이 조금 부족하단 느낌이 들 수 있을 것 같습니다. (개인적으로 그러한 느낌을 많이 받았습니다..) 따라서, 추가적으로 1저자분이 발표한 유튜브 영상을 video 링크로도 남겨두었으니 해당 영상을 참고하시면 조금 더 깊은 이해에 도움이 되지않을까 생각합니다.
  • 또한, official code의 구성이 정말 깔끔합니다. 해당 코드의 notebook을 직접 돌려보시면서 그 결과를 확인해보시는 것도 추천드립니다.

Introduction

• 다들 잘 아시다시피, 컨볼루션 신경망(CNN)은 이미지 이해, 인식 분야에서 뛰어난 성능을 자랑합니다. 하지만 그 특성 상, 비유클리드 공간에서의 불규칙적 데이터 구조를 이해하는 것에는 한계가 존재합니다.
• 그로부터 CNN의 개념을 그래프 개념으로 확장한 GNN (GCNs)의 효과와 그 유연성이 입증되었으며, 더욱 폭넓은 도메인 상에서 그래프 표현 학습의 개념 및 활용 방법 등이 활발하게 연구되어지고 있습니다. 하지만 pairwise relation을 모델링하는 것에 제한되어 있습니다.
  • 다음을 해결하기 위하여 hypergraph neural networks, motif-based GNNs 등이 제안되어져 왔으나, 공간 전역의 그래프가 표현하는 토폴로지 정보를 명확하게 연결짓는 수학적 이론 배경이 부족하다는 한계가 있음을 언급합니다.
  • 다음 사실을 기반하여, Simplicial complex로 표현되는 데이터 토폴로지 구조의 탄탄한 수학적 이론들을 배경삼아 그 위에 구축될 수 있는 Simplcial (convolutional) neural network를 설계해보자는 아이디어 접근으로 시작됩니다.

Proposed method : Simplicial convolution

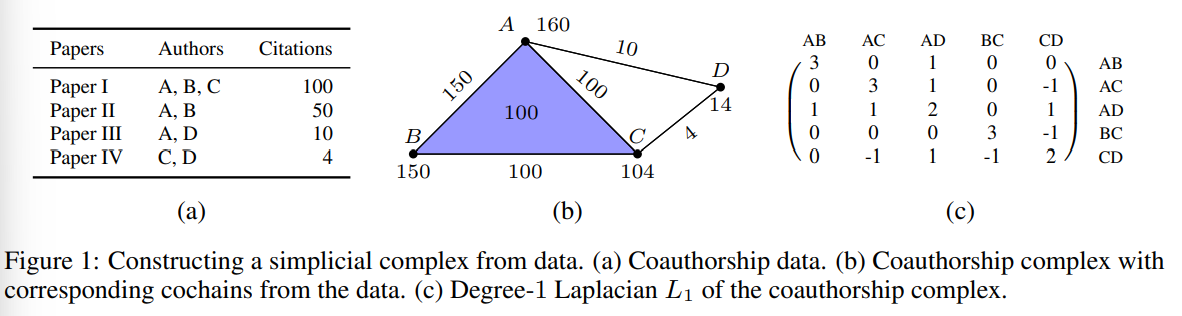
• Simplicial complex 및 Hodge Laplacian 에 대한 배경지식('Simplicial complexes, Simplicial Laplacian' 세션 참고) 내용은 생략하겠습니다.
• 그래프 라플라시안 행렬의 고유분해를 통해 얻어지는 고유 함수(고유벡터, 고유값) 들의 선형조합 꼴에서 정의되는 그래프 푸리에 변환을 활용한 기존 ChebNet의 컨볼루션 연산을 기반으로, 해당 p-Simplicial complex(K_p)의 cochains (C^p)에 대한 스펙트럼 푸리에 변환을 아래와 같이 정의합니다.

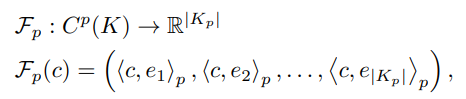
• 여기에서 e_i는 Hodge Laplacian의 고유값에 따라 오름차순으로 정렬된 eigen-cochains입니다.
• F_p(C)는 p-cochain 각각에 eigen-cochains과의 내적 벡터들을 모은 |K_p| 차원의 실수 벡터들의 함수로써 정의됩니다.
• Hodge Laplacian의 diagonalizable한 성질 덕분에, F_p 함수는 invertible하며, 그로부터 그래프 푸리에 변환에 사용되는 고유함수의 꼴로 표현할 수 있게 됩니다.
• 따라서, 다음 푸리에 변환 함수를 활용하여 주어진 Simplicial complex의 cochain을 Spectral domain 상으로 맵핑하여 컨볼루션 연산을 수행할 수 있게 되었습니다. 그로부터 다음의 단순한 형태의 Simplicial Neural Networks(SNNs) 모델을 정의합니다.

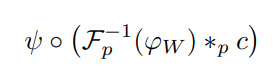
• 여기에서 \phi 표기는 비선형함수를 의미합니다.
• 각 레이어 마다 Localized한 컨볼루션 연산을 보장하기 위해, Chebnet과 유사하게 다음 가중치 함수 (W)를 고유값 기반의 저차 (i) 다항식 꼴로 근사화합니다. 다음은 단순하게 선형 결합 형태로 아래와 같이 정의합니다.

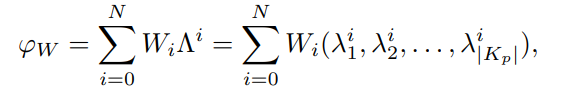
• 결과적으로, 아래와 같은 식을 도출할 수 있습니다.

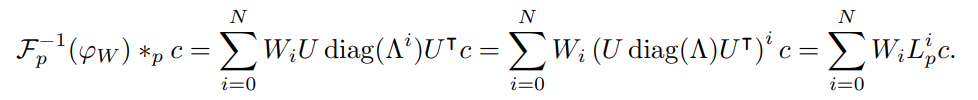
• 간단하게, 입력 p-cochain (c)를 i차수 Hodge Laplacian (i번 거듭제곱 꼴) 및 가중치 행렬을 통해 컨볼루션 연산을 수행하는 것으로 이해해볼 수 있습니다.
• 다시 말하면 Chebnet의 컨볼루션 식에서 라플라시안 행렬을 Hodge Laplacian으로 치환하고, 입력 데이터가 Simplicial complex로 바뀌었다는 것 외에 나머지 연산은 동일한 꼴로 정의할 수 있게 됩니다.
• 저자들은 공저자 (coauthorship) complex (CC, Fig 1(b) 참고)에의 결측 데이터를 처리하는 도메인 상에서 제안 모델 SNNs의 효율성을 실험으로 입증합니다.

Summary

• 이번 주 오마카세는 (가볍게) 그래프 스펙트럼 컨볼루션 개념을 기반으로 Simplicial complex로 확장할 수 있는 컨볼루션 연산자를 정의한, 이후의 많은 Simplicial neural networks 변형 모델들의 모티브가 되고 있는 논문을 소개해드렸습니다.
  • 다음 논문에서는 Simplicial complex 상의 컨볼루션 정의 관련한 핵심 개념들을 간략하게 설명해주고 있기에, 독자 여러분들께서도 부담 없이 이해하실 수 있으실거라 생각합니다.
  • 특히 Chebnet의 내용을 잘 알고계시는 독자분들이라면, 이번 논문의 내용은 상당히 쉽게 느껴지셨을 거라 생각합니다. 그만큼 스펙트럼 그래프 컨볼루션과 깊은 관련이 있으며, 저자들도 Conclusion 부분에서 해당 스펙트럼 개념이 논문 아이디어 전개에 큰 영향을 끼친다고 언급하고 있습니다.
• 하지만 개인적으로, 해당 논문의 설명 만으로 그 내용을 깊게 이해하기에는 어렵다는 생각이 들었습니다. 따라서 저자의 유튜브 설명 및 official code를 참고하여 이해해보고자 하였으며, 그 필요성을 많이 느꼈던 것 같기에.. 다음 논문을 읽으시려는 독자 여러분들께도 추천드리는 바 입니다 !
• 글을 마무리하기에 앞서, 그래프 오마카세를 함께 만들어나갈 마음이 있으신 분들을 구하고 있습니다. 매주 다양한 그래프 주제로 자유롭게 뉴스레터를 연재하는 것에 관심이 있으신 분들께서는 언제든지 제 메일주소로 편하게 연락주시면 감사하겠습니다 !

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn