그래프 튜토리얼 5화 : Graph Convolution Network (GCN)

1. Graph Convolution Network 구현
2. Facebook 데이터셋으로 Link Prediction 좋아요 예측 모델 구현

안녕하세요, GUG 여러분! 그래프 튜토리얼의 가이드 Erica에요🥁

5번째 여행에서는 너무나도 중요하고 유명한 GCN 모델을 다룰 예정입니다. 이 아키텍처를 잘 알아야 하는 이유는, 추후 굉장히 많은 모델에 활용되는 Aggregation 개념이 여기서 처음으로 등장하기 때문이랍니다.

그럼 이제 Graph Convolution Network를 알아보기 위해 떠나봐요!
코드를 한번에 실행해 볼 수 있는 .ipynb 파일은 아래 링크에 있답니다.

GitHub - H4Y3J1N/Graph-Travel: with GUG, Let’s explore the Graph Neural Network!

with GUG, Let’s explore the Graph Neural Network! Contribute to H4Y3J1N/Graph-Travel development by creating an account on GitHub.

GitHubH4Y3J1N

📢 참고로 이번 튜토리얼부터는 코드 전문을 임포트하지 않을 계획이에요.
가독성을 위한 선택이니, 위 링크에서 코드를 확인해 주세요.

# Tutorial Code 실행 환경 및 라이브러리

torch: 2.0.0
torch-geometric: 2.3.1
matplotlib: 3.3.4
numpy: 1.24.3
pandas: 2.0.1
sklearn: 1.2.2
python:  3.10.1

Concept of GCNs

가장 먼저 GCN 알고리즘에 대해 이야기해야겠네요. GCN은 대체 어떤 방식으로 학습하기에 그렇게 유명하고 중요하다는 걸까요?
바로 그건 Node Representation과 Message Passing, 그리고 Aggregation이란 개념 때문이랍니다.

위 3개 개념을 공통적으로 묶는 가장 중요한 점을 딱 한 문장으로 정리하자면,
학습 과정에서 노드끼리 정보를 교환한다는 것입니다. 조금 더 자세히 설명하자면, GCN은 Target Node와 Neighbor Node 사이에서 정보를 교환하는 방식으로 작동합니다.

• 그렇다면 노드끼리 정보를 교환한다는 건 무슨 뜻일까요?
  "노드 간 정보 교환"이란 한 노드가 이웃 노드들의 정보를 수집하고, 그 정보를 통해 새로운 Representation을 만들어내는 것을 뜻해요. 더 쉽게 이야기하자면 Embedding을 업데이트한다는 거죠.
  아래에서 더 자세히 다룰 테지만, degree matrix를 embedding에 곱하는 것은 각 노드의 이웃 정보들을 취합해 target node의 임베딩에 통합하는 과정의 일부분입니다.
  자, 지금부터 이 내용을 확실하게 배워보도록 해요. 이후의 모든 확장 모델들을 손쉽게 이해하기 위해서요!

Node Representation

우리가 앞선 여행들에서 다뤘던 Node Embedding과 동의어입니다. GCNs 모델은 convolution layer를 거칠 때마다 Representation(임베딩)을 업데이트합니다. 이 Representation은 각 노드의 feature vector와 이웃 노드들의 feature vector를 통해 계산돼요.
여기서 계산이란 Representation을 Aggreation하거나 mean하는 과정을 뜻합니다. 이때 Aggreation은 onvolution layer 또는 fully connected layer 등을 통해 이뤄져요.

layer들은 input feature(node representation)를 입력받은 다음, 그것에 가중치를 곱하고, 그 결과에 non linear activation function을 적용해 새로운 representation으로 업데이트합니다.

예를 들어 fully connected layer의 경우, 각 레이어는 이웃 노드 정보와 타겟 노드의 특성을 모두 고려해 각 노드의 임베딩을 업데이트해요. 당연하게도 layer의 weight는 학습 과정에서 최적화됩니다.

Message Passing

embedding 업데이트 프로세스를 한 단어로 간략히 줄여서 Message Passing이라고 합니다. 아주 친절하고 자세히 설명했던 내용을 명료하게 압축해 볼까요?

각 노드가 이웃 노드로부터 정보를 수집하고, 그 정보를 통해 node representation을 업데이트하는 것을 Message Passing Framework라고 합니다.
이것은 각 레이어를 통과할 때마다 수행되고, 레이어를 거칠 때마다 Node는 더 넓은 범위의 이웃으로부터 정보를 얻게 돼요.

Neighborhood Aggreagtion

이제는 "GCNs 아키텍쳐가 Node Representation을 업데이트할 때, Neighborhood Aggregation을 통해 정보를 집계하고, 그렇게 집계한 정보를 Message Passing으로 노드 간 교환한다" 는 문장이 이해되겠네요.

참고로 정보 교환은 레이어를 거칠 때마다 모든 노드에서 동시다발적으로 진행됩니다. 이 방식으로 GCN은 Graph Structure를 이용해 Node Representation을 학습하고, 복잡한 그래프 구조의 패턴을 인식하고 모델링해요.

조금 더 구체적으로 이야기하자면 각 노드는 Adjacency Matrix를 통해 이웃 노드의 정보를 수집하고, Degree Matrix를 통해 이 정보를 정규화합니다.

Task of GCN

이렇게 GCN은 그래프 구조 정보를 적극적으로 활용하기 때문에, Graph Structure와 Node Representation이 중요하게 작용하는 Task에서 특히 뛰어난 성능을 발휘해요.

GCN 모델로 해결할 수 있는 Task로는

1. Node Classification : 유저 특성 예측, 문서 분류 : 주제 예측
2. Node Regression : 노드에 부여되는 이산적인 값 예측
3. Link Prediction : 노드 사이에 엣지가 존재할 가능성 예측, 친구 추천
4. Graph Classification : 그래프 분류 작업

같은 것들이 있답니다.
그리고 이번 여행 튜토리얼에서는 Link Prediction을 직접 진행해볼 거에요!

About Facebook Dataset

Facebook에서 공개한 page-page 오픈 데이터셋을 들여다볼까요?
각 노드는 공식 Facebook 페이지이고, 링크들은 사이트들 사이의 상호 좋아요를 나타내죠. 노드 특성들은 페이지 소유자들이 직접 페이지 설정에 기재해둔 설명으로부터 추출했다고 합니다.
그러니 이 데이터셋을 활용하면 우리는 A 페이지가 B 페이지에 좋아요를 누를 것인지 아닌지를 판단할 수 있어요! 참고로 Multi-class node classification에도 적합한 데이터셋이랍니다.

이런 예측의 경우 시계열성도 중요하게 반영할 수 있을 텐데요, 일단은 GCN을 적용해보는 것이 목표이니 지금은 이 부분을 특별히 신경쓰지는 않을게요. 그 부분은 다음에 다룰 GAT 모델에서 정복해 봅시다!

End - End Model

Graph Convolutional Network과 Linear Neural Network로 구성된 Link Prediction 모델

사실 이번에 구현할 모델은 단순한 GCN 아키텍쳐 하나가 아닙니다. 여기에 Linear 한 신경망 모델을 하나 추가해서, End to End 모델을 만들어낼 거랍니다.

목표는 GCNs 모델을 통해 Node Representation을 완성해 추출해 내고,
간단한 선형 신경망을 활용해 Edge의 연결 가능성을 예측할 거에요!

우선 이번 코드의 주요한 아키텍처부터 설명할게요.
GCN은 노드 특성 x와 edge_index를 input으로 받아 그래프를 학습하고, 각 노드의 업데이트된 Node Representation을 반환합니다.

이후 LinkPredictor가 노드 2개의 표현을 입력으로 받고, 이 두 노드가 연결될 확률을 출력해요. 이 확률은 Sigmoid를 통해 0과 1 사이의 값을 반환하죠. 이 값은 그래프의 노드 쌍 간의 연결 가능성을 예측하는 데 사용됩니다.

 class LinkPredictor(torch.nn.Module):
    def __init__(self, in_channels):
        super(LinkPredictor, self).__init__()
        self.lin = torch.nn.Linear(in_channels * 2, 1)

    def forward(self, x_i, x_j):
        x = torch.cat([x_i, x_j], dim=-1)
        x = self.lin(x)
        return torch.sigmoid(x).squeeze()

LinkPredict 클래스는 두 노드 임베딩을 연결하고, 그 결과를 선형 신경망에 통과시킵니다. 최종적으로 torch.sigmoid 함수를 통과한 값은 0과 1 사이의 확률로 출력해요. 이 결과는 두 노드가 연결되어 있을 가능성을 나타냅니다.

class GCN(torch.nn.Module):
    def __init__(self, in_channels, hidden_channels, out_channels, num_layers, dropout=0.1057085140333304, activation_func=torch.nn.SELU()):
        super(GCN, self).__init__()
        self.layers = torch.nn.ModuleList()
        self.activation_func = activation_func
        self.dropout = torch.nn.Dropout(dropout)

        # 입력 계층
        self.layers.append(GCNConv(in_channels, hidden_channels))

        # 숨겨진 계층
        for _ in range(num_layers - 2):
            self.layers.append(GCNConv(hidden_channels, hidden_channels))
        
        # 출력 계층
        self.layers.append(GCNConv(hidden_channels, out_channels))

    def forward(self, x, edge_index):
        for layer in self.layers[:-1]:
            x = layer(x, edge_index)
            x = self.activation_func(x)
            x = self.dropout(x)
        
        x = self.layers[-1](x, edge_index) # 마지막 계층에서는 활성화 함수와 dropout을 적용하지 않습니다.

        return x

이 클래스는 Graph Convolutional Network를 간단하게 구현한 것입니다.

GCN은 그래프 데이터를 처리하기 위한 Convolutional Neural Network의 변형이에요. 각 노드는 이웃 노드의 정보를 집계함으로써 새로운 특성을 얻습니다.

입력 계층과 숨겨진 계층에서는 각 계층 이후에 SELU 활성화 함수와 dropout이 적용되며, 출력 계층에서는 이들을 적용하지 않습니다. 활성화 함수를 이것저것 실험을 해 본 결과, SULE가 가장 성능이 나았습니다.

layer 개수를 하이퍼 파라미터 튜닝하는 데에 용이하도록 변형을 해뒀답니다.

def train():
    model.train()
    link_predictor.train()

    pos_edge_index = data.train_pos_edge_index 
    neg_edge_index = negative_sampling(
        edge_index=pos_edge_index,
        num_nodes=data.num_nodes,
        num_neg_samples=pos_edge_index.size(1),
    )
    neg_edge_index = neg_edge_index 

    optimizer.zero_grad()

    z = model(data.x, pos_edge_index)  
    pos_pred = link_predictor(z[pos_edge_index[0]], z[pos_edge_index[1]])
    neg_pred = link_predictor(z[neg_edge_index[0]], z[neg_edge_index[1]])

    loss_func = torch.nn.BCEWithLogitsLoss()
    pos_loss = loss_func(pos_pred, torch.ones(pos_edge_index.shape[1], device=device))  
    neg_loss = loss_func(neg_pred, torch.zeros(neg_edge_index.shape[1], device=device)) 
    loss = pos_loss + neg_loss
    loss.backward()
    optimizer.step()

    return loss.item()

validation 함수는 test 함수와 매우 유사하기에 튜토리얼 본문에서 따로 다루지는 않겠습니다! 대신 train 함수와 test 함수를 세밀하게 다룰게요.

train함수의 중요한 코드라인은, pos_edge_index와 neg_edge_index를 정의하는 부분입니다. 이때 negative sampling 함수를 통해 neg_edge_index를 확보합니다.
추출한 node embedding으로부터 Pos/Neg Edge에 대한 예측값을 계산한 다음, Binary Cross Entropy loss를 계산하고, 이를 이용해 각 Pos/Neg Edge에 대한 loss를 계산합니다.
최종 loss는 각 Edge에 대한 loss 값의 합이에요.

손실함수로는 torch.nn.BCEWithLogitsLoss() 또는 torch.nn.BCELoss() 같은 이진 분류 손실함수를 사용할 수 있고, 이 함수는 모델이 예측한 확률과 실제 label(0 또는 1) 사이의 차이를 계산합니다.

참고로 optimizer는 AdamW를 사용했습니다.

def test():
    model.eval()
    link_predictor.eval()

    with torch.no_grad():
        z = model(data.x, data.test_pos_edge_index)
        pos_pred = link_predictor(z[data.test_pos_edge_index[0]], z[data.test_pos_edge_index[1]])
        neg_pred = link_predictor(z[data.test_neg_edge_index[0]], z[data.test_neg_edge_index[1]])

        pos_loss = F.binary_cross_entropy(pos_pred, torch.ones(data.test_pos_edge_index.size(1)))
        neg_loss = F.binary_cross_entropy(neg_pred, torch.zeros(data.test_neg_edge_index.size(1)))
        loss = pos_loss + neg_loss

        # 실제 positive, negative edge의 라벨
        labels = torch.cat([torch.ones(data.test_pos_edge_index.size(1)), torch.zeros(data.test_neg_edge_index.size(1))]).cpu().numpy()
        
        # 예측된 확률
        preds = torch.cat([pos_pred, neg_pred]).cpu().numpy()

        # 이진 분류 문제에서 확률을 기준으로 클래스를 결정
        preds_class = (preds > 0.65).astype(int)

        precision = precision_score(labels, preds_class)
        recall = recall_score(labels, preds_class)
        f1 = f1_score(labels, preds_class)
        roc_auc = roc_auc_score(labels, preds)
        accuracy = accuracy_score(labels, preds_class)
        confusion_mat = confusion_matrix(labels, preds_class)

    print("Test Loss: {:.4f}".format(loss.item()))
    print("Precision: {:.4f}".format(precision))
    print("Recall: {:.4f}".format(recall))
    print("F1 Score: {:.4f}".format(f1))
    print("ROC AUC Score: {:.4f}".format(roc_auc))
    print("Accuracy: {:.4f}".format(accuracy))
    print("Confusion Matrix:")
    print(confusion_mat)

    return loss.item(), precision, recall, f1, roc_auc, accuracy, confusion_mat, labels, preds

test 함수에서 눈여겨봐야 할 점은, Threshold입니다. 코드 라인에서는 Erica가 약간의 실험을 통해 가시적으로 확인한 최적의 값을 넣어 두었는데요, 그게 바로 0.65였답니다.
우리가 만든 GCNs+선형 신경망 모델의 예측값은 0~1 사이의 연결확률을 반환하므로, Threshold를 통해 이 확률을 0 혹은 1. 다시말해 Binary한 값으로 바꿔야 해요.

이렇게 하면 확률이 0.65 이상인 경우 해당 샘플을 긍정적(즉, 두 노드가 연결됨)으로 분류하고, 그렇지 않은 경우 부정적(즉, 두 노드가 연결되지 않음)으로 분류됩니다.

• 그럼 이제 한번 모델을 학습시켜 보고, 성능을 확인해 볼까요?
  참고로 Erica는 hyperopt 라이브러리를 사용해 Baysian Optimizing을 진행했고, 거기서 최적의 파라미터를 찾아냈답니다.

Test Loss: 3.3650
Precision: 0.6855
Recall: 0.6574
F1 Score: 0.6711
ROC AUC Score: 0.7176
Accuracy: 0.6779
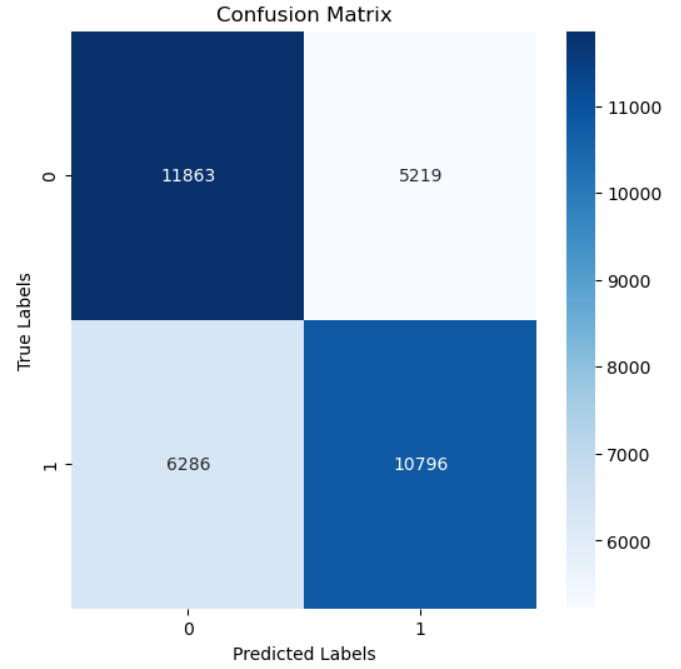
Confusion Matrix:
[[11930  5152]
 [ 5853 11229]]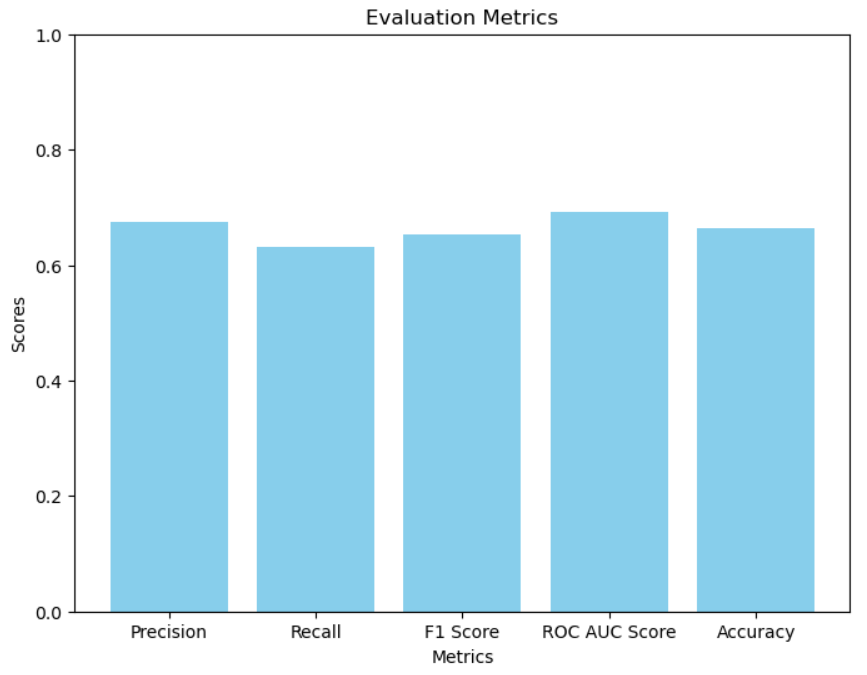

Dataset의 크기가 그리 크지 않아서인지 모델이 간단할수록 성능이 높아지는 경향이 보였어요. 이 시각화 코드 역시 Gitgub Link에서 확인할 수 있답니다.

Graph Travel 튜토리얼이 도움이 되고 있다면,
꾸준한 업로드의 원동력이 되도록 STAR🌟도 한번 눌러주세요~!

꽤 간단한 모델이었는데도 2/3은 맞추고 있다는 점이 놀랍네요. 이게 GCN의 힘이라는 걸까요?

GCN의 메인 컨셉은 이후 확장된 다양한 GNNs 모델들에서 어렵지 않게 발견할 수 있답니다. 그 예시로는 GAT, GraphSAGE 등이 있어요.

🎫 Attention?

다음 여행에서는 조금 더 나아가 Graph AttenTion Network 모델, GAT 의 메인 컨셉을 심층적으로 파헤쳐 보도록 해요!