5월 1주차 그래프 오마카세

GNN popular booms are coming

[그래프 지식 공유를 함께하실 분들을 구합니다.]

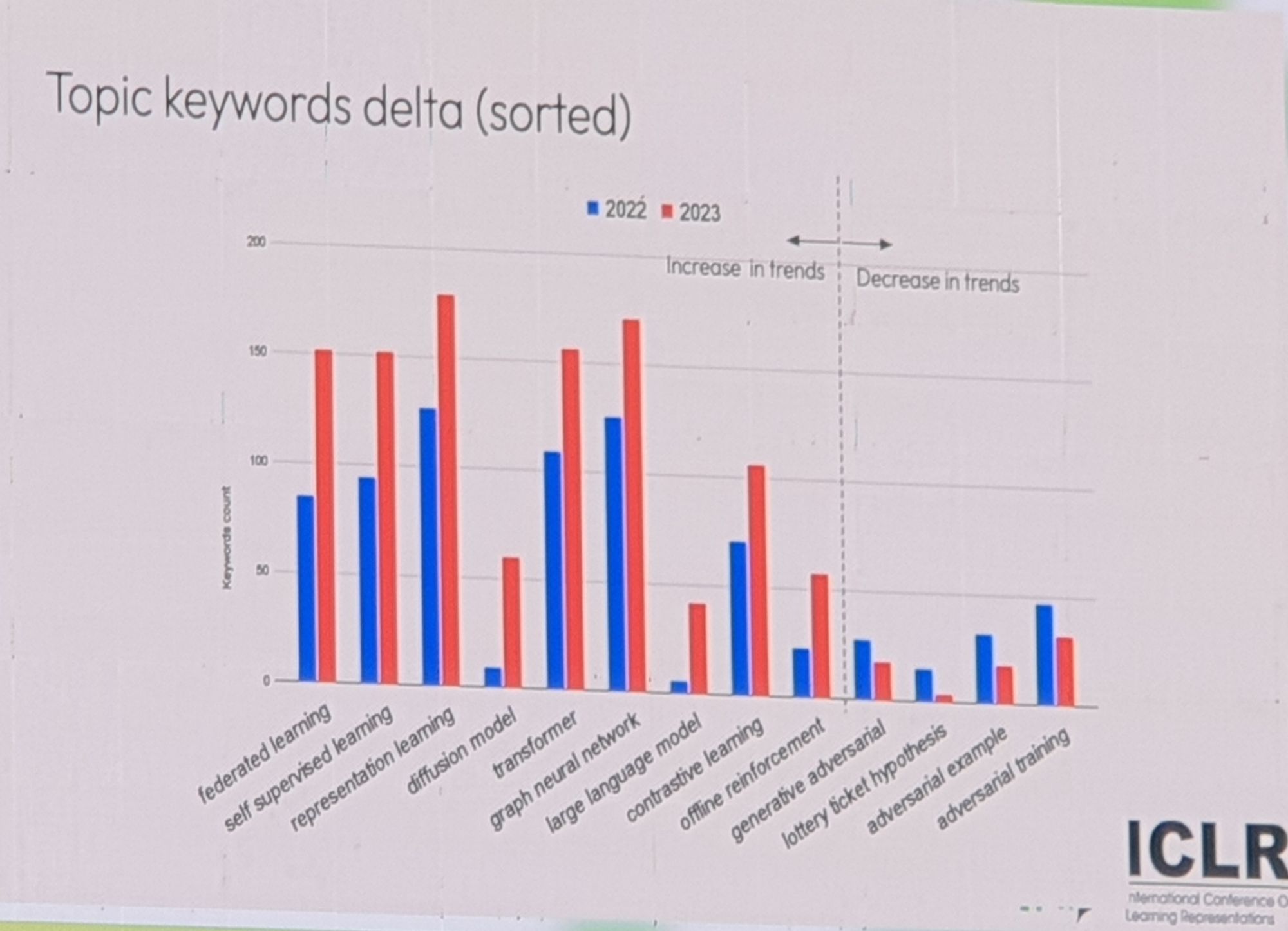
봄이 다가온지가 엊그제 같은데 벌써 여름이 다가옴을 한낮의 더위로 느끼고 있네요. 이와 비슷하게 혹시 여러분들도 GNN 붐이 다가오고 있음을 느끼고 계실까요? 첨부드린 사진의 수치와 같이 2022,2023(twitter @xbresson) 각각 topic keyword 를 비교한 차트를 보시면 눈에 띄게 graph neural network 가 관심을 받고 있음을 알 수 있습니다.

“학계에서만 관심 있을것이다” 라는 생각과 다르게 실제 뉴스레터 , 트위터 , 미디엄 3개의 추이를 직접 확인해보니 이 관심이 “진짜”임을 알 수 있었습니다. 특히, 트위터의 반응은 폭발적이였는데요. 뉴스레터(그래프오마카세) 관련 이야기 적은 게시물이 하루만에 노출수 3만 참여수 800여명 등의 수치를 보였습니다. 뿐만아니라, 그래프 뉴스레터를 시작한지 6개월 가까이 된 지금 구독자 200명을 앞두고 있네요.

이 수치를 통해, 그래프에 대한 관심이 학계뿐만 아닌, 실제 현업 및 타 도메인(블록체인, 금융 등)분들께서도 많이 있으심을 깨달았고, 관련 정보를 공유하기에 좋은 커뮤니티를 개설해보았습니다.

커뮤니티 링크는 다음과 같습니다. https://www.graphusergroup.com/

커뮤니티 콘텐츠 박스는 다음과 같이 크게 3가지로 구성했습니다.

1.그래프 오마카세 , 2.그래프맨 , 3.그래프인터뷰

1은 그래프 데이터 베이스 , 그래프 딥러닝 , 그래프 이론 관련 소식을 뉴스레터 형식으로 제공하는 콘텐츠 입니다.

2는 그래프를 활용해서 실제 문제를 해결하는 솔루션 박스를 담는 공간입니다.

3는 그래프를 활용하고 계시는 학계 , 산업계분들과 인터뷰를 한 내용을 담는 공간입니다.

위 3가지 콘텐츠 박스를 채워가는 과정에 함께하실분들을 구합니다! 현재 국내 5분 , 해외 5분 총 10분을 모집할 예정입니다. 많은 관심 및 신청 부탁드립니다 ! 바쁘신 와중에 긴 글 읽어주셔서 감사드립니다.

GL2vec: Graph Embedding Enriched by Line Graphs with Edge Features

[https://dl.acm.org/doi/10.1007/978-3-030-36718-3_1]

Introduction

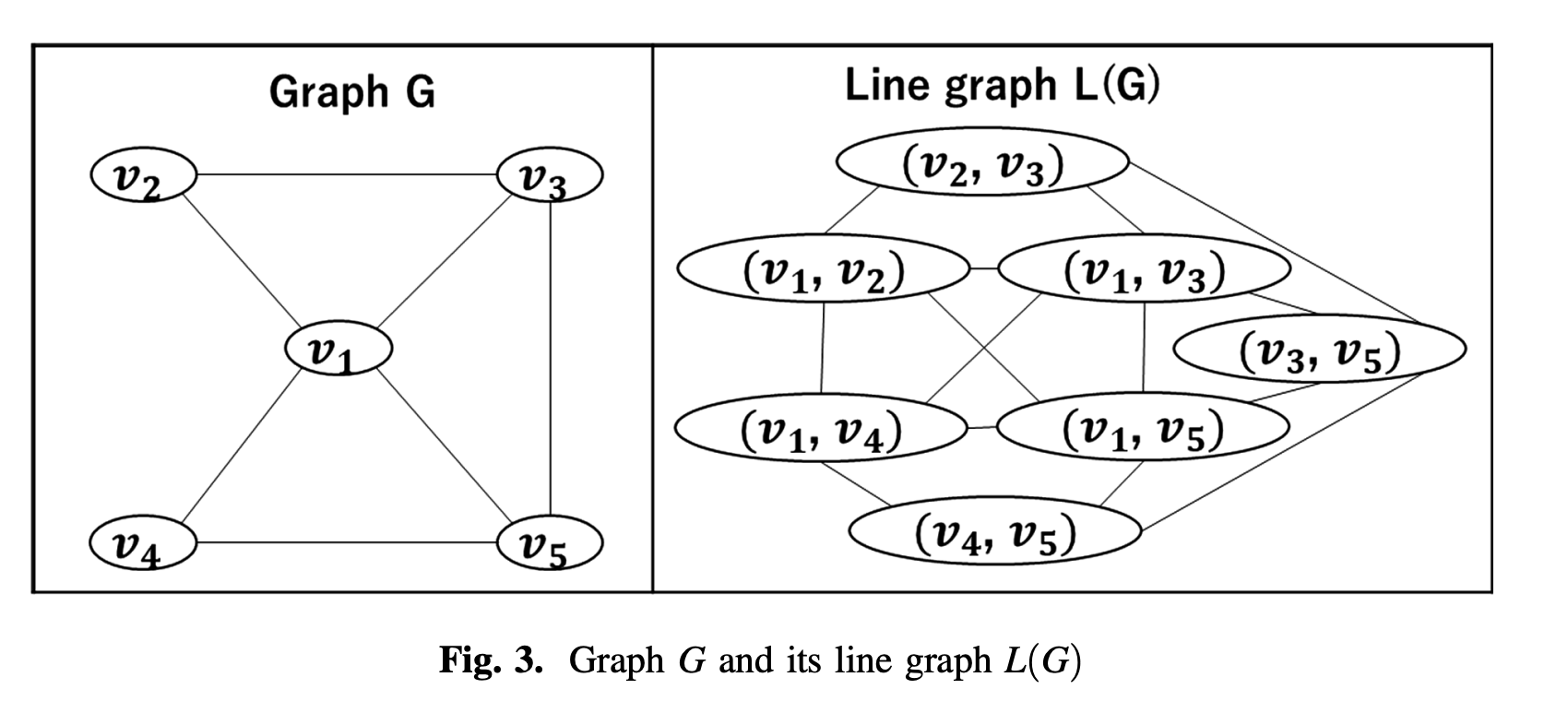
그래프 임베딩의 조상격인 Graph2vec의 단점을 보완한 논문 GL2vec 입니다. 기존 Graph2vec에서는 노드(node) label information만을 활용하여 임베딩합니다. 하지만 그래프는 노드 뿐만아니라, 엣지도 존재합니다. Graph2vec은 ‘노드’ 정보만을 고려하고 엣지에 대한 정보를 고려하지 않기에 엣지에 담긴 속성이 중요할때에는 그 중요도를 반영하지 못한다는 한계점이 존재합니다. 이 한계점을 극복하기 위해 논문 저자는 linegraph를 활용한 아이디어를 제시합니다.

Preliminary

Linegraph , Graph 요소인 노드와 엣지를 바꾼 개념이라고 보시면 되겠습니다. 노드와 엣지를 바꿈으로써 엣지로써 연결된 각각의 두 노드를 하나로 간주합니다.

Summary

‘’’nx.line_graph()’’’ 기존 graph2vec 과 구현 코드와 다른 한 줄 입니다. 이외의 코드는 모두 동일합니다. Weisfeiler-Leman algorithm를 적용해서 고유 structure feature 를 추출하고 그 정보들을 종합해서 documentation 형태로 전환 뒤, doc2vec을 적용하며 임베딩을 마무리 합니다.

Insight

노드 , 엣지 attributed 를 적용 전/후에 따라 성능이 어떻게 바뀌는지에 대해 궁금하셨던 분들 , 레퍼런스가 필요하셨던 분들 대상으로 인사이트를 제공할 수 있는 논문이라 생각합니다.

Graph Kalman Filters

[https://arxiv.org/pdf/2303.12021.pdf]

Introduction

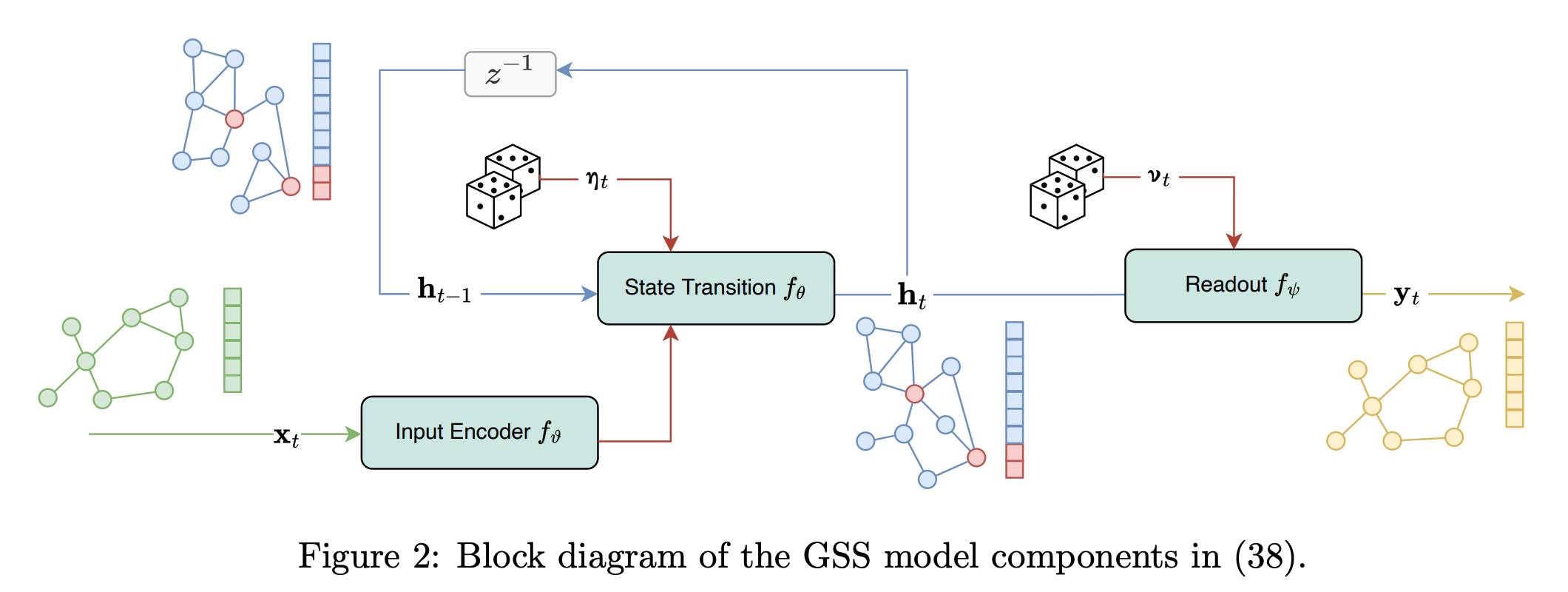
칼만 필터, 다들 한번쯤은 들어보셨을 알고리즘이라 생각합니다. 과거 현재 상태를 기반으로 미래 상태를 예측한다는 관점. 본 논문은 칼만 필터 관점을 그래프에 접목합니다. 구체적으로는 graph attribute 인 노드, 엣지(topology) 가 시간(noise)에 따라 어떻게 변하는지를 측정한다 라고 보시면 되겠습니다. 기존 칼만필터와 다르게 readout(graph 정보 종합) 하는 layer 가 추가되었다는 점을 제외하고는 뚜렷한 다른점은 없어보입니다.

Preliminary

Kalman Filters

The Kalman filter is an algorithm used for estimating the state of a dynamic system based on noisy or incomplete measurements. It operates recursively, continuously updating the state estimate as new measurements become available.

보다 자세한 내용은 JINSOL KIM 님의 ‘https://gaussian37.github.io/ad-ose-lkf_basic/’ 포스팅을 보시는것을 추천드립니다.

Summary

white noise 를 node signal 에 넣어줌에 따라 어떻게 topology가 변하는지를 stochastic 하게 파악합니다. 노드 , 그래프 각각 n_t , v_t noise 를 넣어주어 그 변화를 측정하는데요. 이 변화를 모두 저장하지 않고, 대략적인 공변하는 값(prior - posterior)을 추출한 뒤 그 값을 활용하기 때문에 연산량 측면에서 효율적입니다.

Insight

temporal learning 에서 핵심 중 하나는 실시간성으로 등장하는 노이즈들을 잘 판별하여 예측하는 것인데요. 이전의 히스토리를 모두 재학습하고 예측하기에는 연산량이 상당하여 리소스가 부담이 되는 경우가 많습니다. 이 경우 정확한 예측 보다 대략적인 맥락을 파악한다 라는 느낌, 1차 필터링 한다는 느낌으로 적용을 시도하실때 본 논문 아이디어를 차용하시는 것도 좋아보이네요.

DiffWire: Inductive Graph Rewiring via the Lovász Bound

[https://arxiv.org/pdf/2206.07369.pdf]

Introduction

고질적인 문제 under-reaching , over-smoothing, over-squashing 3가지를 해결하기 위해 본 논문에서는 그래프 재연결(graph rewiring)을 제안합니다. graph rewiring 이라는 다소 낯선 개념이 등장해서 논문이 어색하실수도 있을거라 생각됩니다. 하지만, 네트워크 과학에서 많이 마주친 커뮤니티 디텍션(community detection)에서 자주 마주하는 modularity metrics 의 관점과 유사하다고 생각하시면 되겠습니다.

간단히 말씀드리면, 그래프 내 노드의 기존 연결을 제외하고 타 노드를 연결했을시 정보 획득량 측면에서 얼마나 유용한가 를 최적화하는 기술이라고 보시면 되겠습니다. 조금 더 디테일하게 말씀드리면 over-squashing 문제를 그래프 구조 변형을 최소화하며 그래프 재연결을 하는 아이디어가 본 논문의 핵심이라고 보시면 되겠습니다.

Preliminary

본 논문을 읽기 위해 연관된 사전 배경지식들이 너무 많아 따로 제시해드리기엔 어려울 거 같네요. 반대로 생각해보면, 그만큼 본 논문이 네트워크 과학(network science) 에서 중요한 개념들이 많이 포함되어 있음을 알 수 있습니다. GNN 트랜드를 네트워크 과학 측면에서 어떻게 해결했는지 궁금하신 분들을 꼭 보시는걸 추천드립니다.

Summary

2가지 레이어가 본 아이디어의 핵심이라고 할 수 있습니다.

CT-LAYER는 commute time를 학습하여 그래프 구조 분포 변화를 최소화하며 정보를 고루고루 전달할 수 있는가를 layer화했다고 보시면 되겠습니다. 주로 circut (반도체설계)에서 활용되는 유효 저항 Effective resistances관점을 접목해서 어떤 노드와 노드를 연결하면 정보가 최소가 되는지 최대가 되는지 (lovász bound)을 지정하고, bound 에 따라 에너지의 변화율인 Dirichlet energy 가 어떻게 달라지는지를 측정하여 boundary gap 을 최소화합니다. 이 과정을 반복하다보면 최적의 bound 를 추출하게 되고 그 내에서 sampling 된 결과들은 구조 분포는 최적화되어 있으나 , 정보는 잘 교류되는 new graph 가 만들어지는거죠.

GAP-LAYER는 네트워의 분포인 spectral gap을 최적화합니다. spectral gap의 기준은 Fiedler vector를 활용합니다. 다시 말하면 cost function 의 기능을 Fielder vector 로 활용하는거죠. 참고로, Fielder vector 는 second smallest eigenvalue of the Laplacian matrix of a graph. 를 의미합니다. 그래프 구조를 표현하는 매트릭스 중 최대 정보를 보존하고 있는 eigenvalue 라고 보시면 되겠습니다. 본 레이어 GAP-layer 에서는 위에서 언급한 cost function을 최적화 하기 위해 , 적절한 cutting (Ratio-cut)을 활용합니다.

이전 CTlayer에서 샘플링을 하는것과 다르게 직접적으로 cutting 함으로써 직접적으로 구조 분포에 개입합니다. 또한 노드와 노드간 정보구조인 commute time 을 측정하는 CTlayer , 그래프 자체 정보구조를 적용하는 Rcut 을 활용함으로써 , 거시미시적인 측면 모두를 고려하여 Rewiring 한다고 보시면 되겠습니다.

Insight

기술 면접에서 자주 활용될 개념이라 생각합니다. 만약 회사에 GNN 관련 jd 를 내놓았고, 지원자가 왔을시 물어보면 좋을만한 기초 개념들을 잘 다루어 놓았습니다. 현업에서 많이 마주하는 문제들을 해결할 수 있는 방안의 토대가 되는 중요한 개념들을 논문에 잘 담아놓았기에 거듭 추천드리는 논문이라 생각되네요.

위 논문 DiffWire 가 이론적인 요소에 집중했다면, 아래 포스팅은 머신러닝 엔지니어가 보면 좋을 실용적인 요소에 집중하고 있습니다. 결은 비슷하나 목적이 다르기 때문에 목적에 따라 취사 선택하시어 보시는걸 추천드립니다.

Scaling GNNs with Graph Rewiring

[https://medium.com/@vp1865/scaling-gnns-with-graph-rewiring-9531be144add]