24년 7월 2주차 그래프 오마카세

Position: Topological Deep Learning is the New Frontier for Relational Learning

ICML 2024

배지훈

paper link : https://openreview.net/forum?id=Nl3RG5XWAt

• 이번 주 그래프 오마카세부터는 조금 새로운 개념의 토픽을 가지고 GUG 구독자 분들께 제공해 드리고자 합니다. 'Topology' 관점에서 기존의 그래프 개념을 확장시키고 노드 간 pairwise-relationship 뿐만 아니라 그 이상의 higher-order components 간의 relationship을 한번에 고려할 수 있는 방법을 소개해드리고 싶습니다.
• 그래프 표현 학습 (Graph representation learning, GRL) 및 기하학 딥러닝 (Geometric deep learning, GDL)은 다양한 도메인 상에서 주어진 객체 상, 객체 간의 복합적인 관계성을 잘 포착하는 능력을 기반으로 해당 GNNs 모델 학습을 통해 downstream tasks에서 인상적인 성능을 보장할 수 있는 방법으로 각광을 받고 있습니다. 필자 개인적으로는 특히 3D Computer Graphics에서 관심 객체의 모양, 형태 등에 대한 좀 더 구체적인 feature selection을 요구하는 tasks 성격에 맞추어, 확장된 개념의 그래프적 표현을 선호하게 되었습니다.
• 결론적으로, higher-order relationship을 고려할 수 있는 networks로 충분히 생각해볼 수 있는 TDL 개념을 독자 여러분들께 소개해드리고, 같이 고민해보고, 많은 인사이트를 얻어갈 수 있는 글 연재를 시작해보고자 이렇게 서두를 작성해보았습니다.
• 이번 주 오마카세로 제공해드릴 논문은 'Position: Topological Deep Learning is the New Frontier for Relational Learning' 이름의 TDL survey 논문으로, 최근 많은 각광을 받고 있는 TDL 및 TDA에 대한 특성, 장점, 한계점 등등을 자세하게 풀어내고 많은 연구자들에게 잠재성을 잘 강조해주었다고 생각하여 선택하게 되었습니다.

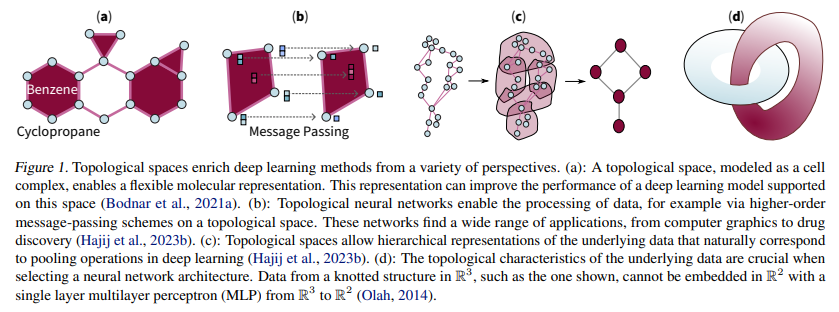
• 토폴로지의 개념은 연속적인 변형 프로세스에서도 불변성을 유지하는 속성에 대한 연구로 생각할 수 있으며, 주어진 데이터의 Global structure를 얻어낼 수 있는 강력한 도구로 사용될 수 있습니다. 대표적으로 Persistent homology가 있는데, 다음은 앞으로 천천히 살펴보도록 하겠습니다.
• 데이터의 토폴로지 특징을 활용하여 신경망 내부의 정보 흐름을 이해하고, 연산 동작에 대한 새로운 인사이트를 얻을 수 있는 등 연산 모델의 전체적인 메커니즘을 이해하고 목적에 맞게 컨트롤할 수 있습니다. 예를 들어, 메세지 전달 메커니즘을 기반으로 그래프 전체로 전달되는 특징의 흐름 (feature flow)을 학습된 표현 정보의 토폴로지 특성을 해석하고, 그로부터 또다른 향상된 혹은 제약된 학습 메커니즘으로 발전시키어 전체적인 모델 성능을 향상시킬 수 있습니다.
  • 그만큼, 데이터의 토폴로지 정보를 파악 및 활용하는 것은 굉장히 유용하며, 실제로 많은 real world application에서 적절히 적용될 수 있음을 암시합니다.
  • Fig 1 (a)의 대표적인 단백질 구조 예측에서 해당 토폴로지 공간에 놓여진 단백질 요소의 개별적인 토폴로지 표현정보를 기반으로 딥러닝 모델의 성능을 향상시킬 수 있음이 밝혀졌으며, (b)의 pairwise한 메세지 전달 메커니즘을 higher-order 메커니즘으로 확장시켜 drug discovery와 같은 유용한 어플리케이션에 활용시켜볼 수 있습니다.
  • 그 외에도 (c)의 그래프 클러스터링, 풀링 방법에 활용될 수 있고, (d)의 저차원 임베딩 함수 및 네트워크의 표현적 한계점을 해결하고 대체되어 활용 가능한 새로운 네트워크 구축에도 활용될 수 있습니다.

Why TDL?

• 저자들은 '왜 TDL?'이라는 가장 근본적인 질문에 대한 해답을 TDL의 특성에 맞추어 찾고자 합니다. 왜 관계형 데이터에 대한 인코딩, 모델링, 그리고 분석 측면에서 TDL이 중요한 역할을 담당할 수 있는가? 에 대한 이유를 아래와 같이 정리합니다.
• 먼저, 주어진 데이터 공간에서의 토폴로지 정보는 적절한 신경망 아키텍처의 선택에 도움을 줄 수 있고, 단순 관계성을 확장하여 고차원 관계정보를 폭넓게 활용하여 데이터를 모델링할 수 있습니다. 이름 그대로, 관계형 데이터 사이에 드러나는 토폴로지 특성들을 중점으로 고려하기 때문에 위의 장점들을 기반으로 다양한 문제점에서의 적용 flexibility를 확장시킬 수 있고, 데이터에서의 토폴로지 등변성(topological equivariance)을 추출하는 데 활용될 수 있습니다.
• 특히 higher-order domains 상에 제공되는 데이터를 처리하기 위한 딥러닝 아키텍처를 구축할 수 있도록 하는 몇가지 주요 fashion이 존재합니다.
  • Simplicial complex
  • Cell complex
  • Hypergraph
• 다음 방법으로 표현된 데이터의 시각화 결과를 분석하여 다양한 관점에서 학습 과정을 해석하고, 그로부터 적절한 모델 아키텍처를 선택할 수 있는 기준을 제시할 수 있습니다.

" 시스템으로부터 주어지는 데이터 상의 binary (pairwise) 혹은 higher-order relation의 상호 연결 특성은 관계형 데이터로 인코딩되어지며, 이러한 데이터를 학습할 수 있는 프레임워크로써 TDL을 고려할 수 있습니다. 즉, TDL은 관계형 학습에서 새로운 지평선을 제공합니다."

• 그 외의 TDL Dataset, Software, Computational beneifts 등등의 자세한 설명은 글의 복잡성을 줄이기 위해 생략하고, (관심이 있으신 독자분들은 해당 논문을 꼭 정독해보시는 것을 추천합니다.) Chapter 6의 Theoretical Foundations에 집중해보셔도 좋을 것 같습니다.

Why is topology relevant in deep learning?

When do higher-order relations become useful?

What are the advantages of TDL over GRL?

• 다음 질문들은 TDL의 상대적인 이점을 강조하는 데 밝혀야 할 중요한 문제이자 마련해야 하는 이론적 토대의 근본적인 질문으로 바라볼 수 있습니다.
• 토폴로지 관련성 및 higher-order relations으로부터 얻어진 downstream의 성능에 대한 맥락적 이해를 밝히기 위한 이론적 연구들이 활발히 이루어지고 있습니다.
  • Signal processing of Higher-order networks (TSP)
  • Hodge Theory & Laplacian for TSP
  • Sheaf Thoery for TDL
  • Generative TDL
• 위의 잘 구축되어진 이론적 토대는 TDL의 속성을 연구하고 분석하는 데 매우 중요한 역할을 수행하게 될 것이며, 전통적으로 꾸준히 연구되고 잘 정의되어진 GNNs의 (스펙트럼) 특성들을 넘어서 TDL의 상대적 이점들을 얻어낼수 있을 것임을 강조합니다.
• 저자들은 아직 해결해야 할 수많은 Open problems을 다음 논문에서 제공하고 있습니다. 이로부터 관련 연구자들의 연구적 motivation을 이끌어내고 향후 발전해나갈 TDL의 방향성을 잘 제시해주고 있기에, 이 부분도 참고하여 읽어보시면 정말 좋을 것 같습니다.
• 끝으로, 이후의 내용은 오늘 오마카세에서 간략하게 제공해드린 TDL의 이론적 토대를 마련하는 다양한 연구들을 소개하고, 특히 그래프 신호처리 (GSP)의 근본뿌리가 되는 그래프 라플라시안의 higher-order relations으로의 확장 버전인 토폴로지 신호처리 (TSP)의 Hodge Laplacian에 대해 집중적으로 다뤄볼 생각입니다.
• 그 외에도 TDA 관련한 내용 (Homology, filteration etc)들도 꾸준히 다루어볼 생각입니다. 저와 같이 토폴로지의 매력과 고차원 그래프 표현 방법들에 깊게 Dive 해보면 좋겠습니다 !

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn