GraphOmakase

24년 10월 1주차 그래프 오마카세

GUG와 함께 성장하실 분 계실까요!?

GUG의 주요 콘텐츠인 그래프 오마카세는 2022년에 첫 발행을 시작으로, 현재까지 200편 이상의 논문 리뷰를 진행하며, 초기 50여 명의 구독자에서 현재는 493명의 구독자와 함께 폭발적으로 성장하고 있습니다.

본인의 연구나 평소 공유하고 싶은 그래프 지식이 있으신 분이라면, 그래프 오마카세와 GUG를 통해 그래프 기술 생태계에 기여해보시는 건 어떨까요?

그래프 오마카세뿐만 아니라, 지금까지 4번의 오프라인 세미나와 세계 유수의 그래프 전문가들과의 네트워킹을 통해 온라인 세미나도 주최하고 있습니다. 최근에는 GraphRAG에서 자주 언급되는 회사인 Kùzu의 CEO와 온라인 세미나를 개최하며, 해외 그래프 기술 트렌드를 국내에 적극적으로 전달하고 있습니다.

이 모든 것이 가능했던 이유는 GUG 운영진 덕분인데요, 현재 6명의 운영진이 주기적인 온·오프라인 모임을 통해 그래프 커뮤니티 운영 방안을 함께 고민하고 반영한 덕분이라 생각합니다.

이 과정을 함께 경험하며, 그래프 지식을 공유하고 커뮤니티 운영에 참여하고 싶은 분들이 계시다면 함께 하시는 건 어떠신가요?

graphusergroup@gmail.com 로 연락주시면 회신드릴게요! 많은 관심 부탁드립니다!

배지훈

Graph Convolutions Enrich the Self-Attention in Transformers!

paper link : https://arxiv.org/abs/2312.04234

Index

Self-Attention and Graph Convolutional Filter (Relationship)
Graph Filter-based Self-Attention Layers (Methodology)

탑티어 컨퍼런스 Neurlips 2024의 결과가 발표되면서, 수많은 억셉 논문들 관련한 글들이 여러 커뮤니티 상에서 소개되고 있습니다. 그래프 관련한 인상적인 연구 결과들도 정말 많이 나온 것 같은데요. 이번 주 오마카세에서는 다음 이름의 재밌는 논문 하나를 찾아서 읽어보고 전달해드리고자 합니다.
논문 제목 그대로, BERT와 같은 깊은 레이어 층으로 구성되어 있는 대표적인 트랜스포머 모델들의 핵심 모듈인 셀프 어텐션의 문제점 (e.g. Oversmoothing)을 그래프 신호 처리 (GSP) 관점에서 그래프 필터의 재설계 방향으로 연결지어 간단하면서도 효율적인 아이디어를 통해 이를 완화할 수 있음을 보여주고 있습니다.
Graph-filter-based self-attention (GFSA) 이름의 제안 아이디어는 특정 분야에만 국한되어 적용될 수 있는 것이 아니라, 매우 폭넓은 도메인 (e.g. computer vision, natural language processing, graph regression, speech recognition, and code classification)에서 성능을 개선하는 효과를 거둘 수 있음을 보여줍니다. 초기 자연어 처리쪽으로 제안된 트랜스포머가 지금은 다양한 도메인으로 확장되어 꾸준히 좋은 성능을 보여주는 능력을 똑같이 확인해볼 수 있습니다. (Fig 1)

💡

We interpret the original self-attention as a simple graph filter and redesign it from a graph signal processing (GSP) perspective.

Self-Attention and Graph Convolutional Filter

트랜스포머의 핵심은 셀프 어텐션 모듈입니다. 여러분들도 잘 아시다시피 아래의 식으로 정의됩니다.

Self-attention mechanism (SA)

Self-attention matrix (bar_A)

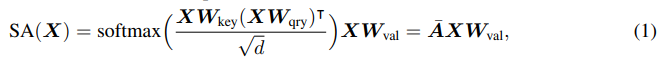
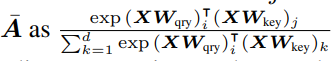
트랜스포머의 입력으로 받는 토큰 시퀀스를 방향성 가중 그래프(directed weight graph)의 노드 시퀀스로, 두 노드의 연결 엣지의 가중치를 해당 어텐션 가중치로 고려해보면, 식 1의 어텐션 행렬인 bar_A를 쉽게 그래프 필터 (H), 구체적으로 K차 다항식 꼴의 linear graph shift operator (S)로써 대체할 수 있음을 확인할 수 있습니다. (식 3)

여기에서 directed graph의 asymmetric한 인접 행렬로부터 고유값 (Eigenvalue) 분석이 아닌 특이값(Sigular value) 분석을 적용하여 directed graph 상의 저주파수/고주파수 신호에 대한 low/high-pass 필터 특징을 조사합니다.
이와 관련한 자세한 설명을 본 논문의 Appendix C에서 제공하고 있으니, 해당 부분을 가볍게 읽어보시는 것을 추천드립니다 !

저자들은 식 1과 식 3의 정의를 통해, 그래프 필터 H를 어텐션 행렬 bar_A로 대체하여 동작하는, 단순하지만 효율적인 GFSA layer 모듈을 제안합니다.

Graph Filter-based Self-Attention (GFSA) Layers

구체적으로 식 1의 bar_A 행렬을 식 3의 다항식 꼴의 linear graph shift operator (S)로 표현하는 방법에 대하여 설명합니다. 그리고, 설계된 그래프 필터의 low/high-pass 성분을 조사합니다.

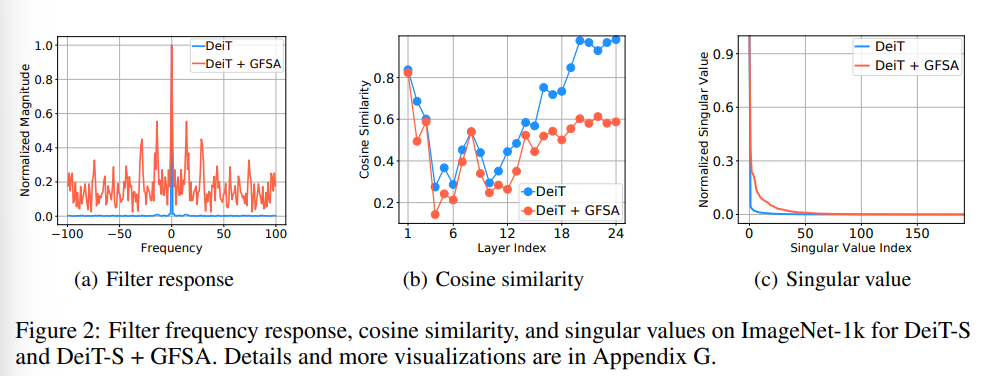
Fig 2(a)의 Filter response 부분을 살펴보면, 기존 트랜스포머 모델 (예시:DeiT)은 델타 함수 꼴의 low-pass filter로만 동작하고 있으나 GFSA를 추가한 모델은 low/high-pass filter로써 모든 신호를 포착할 수 있음을 확인할 수 있습니다.
또한 Fig 2(b)의 Cosine similarity 부분을 보면, 높은 유사도를 보이는 low-frequencies만을 갖고 있는 DeiT와 달리, 약간 떨어지는 유사도를 보이는 high-frequencies도 내포하는 GFSA의 결과 그래프를 통해 위의 사실을 다시금 확인해볼 수 있겠습니다.
마지막 Fig 2(c)의 특이값 그래프를 통해서, 중요하지 않은 거의 0에 가까운 특이값 요소들이 단일 DeiT 모델의 특징 분포에 지배적으로 존재한다는 사실을 확인시키며 쉽게 Oversmoothing 문제에 노출될 수 있다는 사실을 보여줍니다. 하지만 GFSA의 추가로 좀더 유의미한 특이값 요소들을 발견할 수 있으며, 그로부터 자연스러운 성능향상에 도움이 되는 효과를 얻어낼 수 있겠습니다.
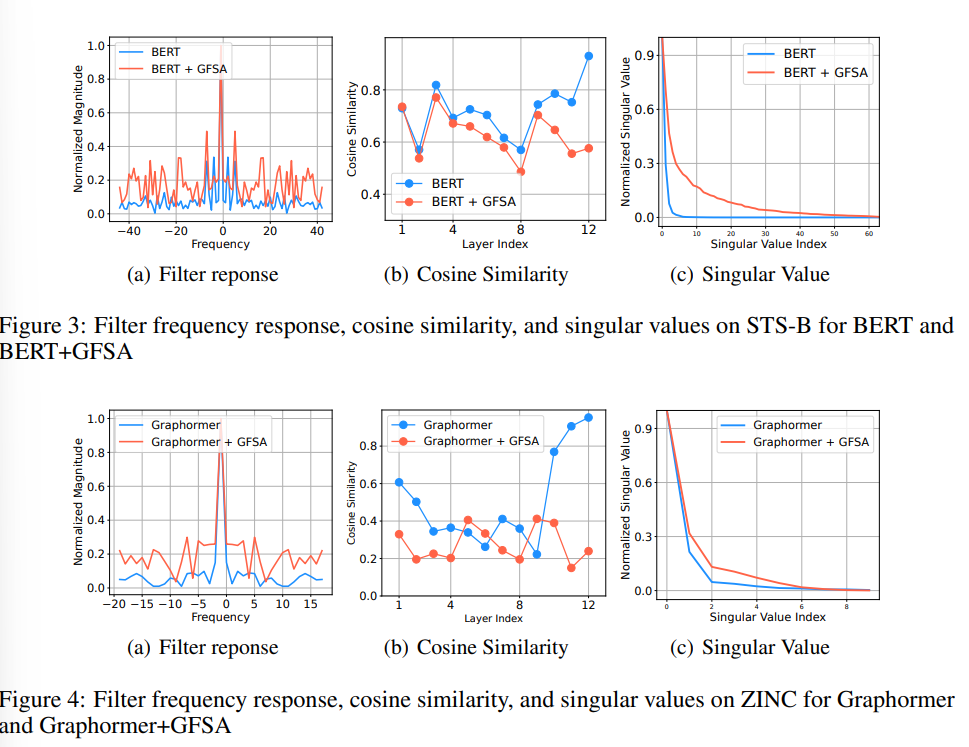
- 트랜스포머 모델 뿐만 아니라, BERT 및 Graphormer 모델에서도 동일한 결과를 Fig 3,4를 통해 확인해볼 수 있습니다.

저자들은 다음의 스펙트럼 특징을 식 4와 같이 정의된 2가지 낮은 차수의 계수 (w_0, w_1) 및 가장 높은 차수의 계수 (w_K) (그 외의 계수들은 모두 0)만을 갖는 필터를 기반으로 분석합니다.

Proposed graph filter (H_GFSA)

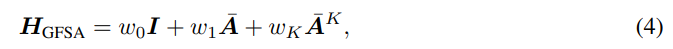
Theorem 3.1에서 저자들은 w_1, w_K가 양의 부호를 갖는 경우 해당 필터 H_GFSA는 low-pass filter로써 동작하며, 음의 부호를 갖는 경우 high-pass filter로써 동작하는 사실을 증명합니다.

Appendix E에서 해당 사실을 자세하게 설명하지만 간략하게 요약하자면, 위의 'Self-attention matrix (bar_A)' 그림을 통해 bar_A은 symmetric normalized adj matrix입니다. 즉, 행의 모든 요소들을 더하면 1을 만족하는 row stochastic matrix이기 때문에, 다음의 특이값 분해를 통해 얻어낸 특이값(\sigma)은 0이상 1이하의 내림차순 분포를 갖게 됩니다.
w_1, w_K가 양의 부호를 갖는 경우, 그로부터 K차수 w_k의 term은 감쇠되어 고주파수 요소를 필터링하는 효과를 갖게 하므로, low-pass filter로써 동작한다고 볼 수 있겠습니다.
마찬가지로 음의 부호를 갖는 경우, 해당 필터가 감쇠되는 신호의 부분을 강조하는 효과를 가지기 때문에 반대로 high-pass filter로써 동작한다고 볼 수 있겠습니다.

Oversmoothing 문제는 레이어 깊이가 깊어질수록 모든 노드 특징값이 유사해져버리는, 즉 반복적인 low-pass filter 적용으로부터 높은 유사도의 low-frequencies components만 남게 되는 결과와 동일한 현상으로 바라볼 수 있습니다.
- Fig 2(a, b)의 DeiT의 필터 응답 그래프를 통해서 low-pass filter로써 동작하는 셀프 어텐션 모듈 기반의 트랜스포머 모델은 다음 문제에서 벗어날 수 없게 되지만, GFSA를 추가한 트랜스포머 모델은 완화할수 있는 능력을 부여받는다는 사실로 쉽게 해석해볼 수 있겠습니다.
하지만, 특이값 분해를 최대 K번 반복해야 하는 연산 비용은 매우 크다는 문제점이 있습니다. 그로부터 다음 고차수 term 부분을 근사화하기 위해, 저자들은 1차 테일러 근사 및 forward finite difference method를 활용하여 다음 문제를 해결합니다.
결론적으로, Oversmoothing 문제와 연산 비용의 완화를 위한 근사화 방법론을 모두 결합한 최종 GFSA 모듈은 식 10과 같이 정의합니다.

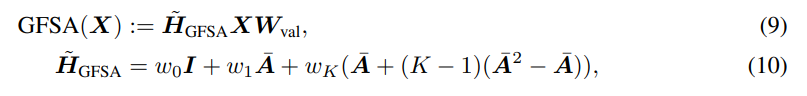
저자들은 i) language understanding and causal language modeling, ii) image classification, iii) graph regression, and iv) code classification의 폭넓은 도메인에서의 실험 결과들을 제공함으로써 제안 GFSA의 효과를 검증합니다. 자세한 실험 결과 및 분석은 해당 논문을 확인해주세요.

본 논문에서는 BERT와 같은 깊은 트랜스포머 모델의 관점에서 Oversmoothing 문제를 해결하기 위해 저자들은 Directed weight graph의 신호처리 관점에서 셀프 어텐션의 low-pass filtering 동작을 특이값의 고유한 성질을 활용하여 high-pass filtering을 가능하게 그래프 필터 재설계를 통해 위의 문제를 완화시키고자 하였습니다.
또한 테일러 근사 방법을 활용하여 일반적으로 연산량이 매우 큰 GSP의 문제점을 해소하고, 식 10과 같이 단순한 형태로 트랜스포머의 셀프 어텐션 부분을 향상시키는 GFSA 레이어 모듈을 제안하였습니다.

Appendix B에서 제공하는 pseudo code의 구성만 보아도, 전체적으로 매우 단순한 아이디어임에도 복잡한 기존 트랜스포머 및 변형 모델들의 내부 모듈을 그래프 관점에서 효과적으로 향상시키고, 최근 핫하게 떠오르는 GPT 계열 LLM 모델까지도 향상된 성능을 보였다는 점이 흥미롭게 읽혔던 것 같습니다.
참고로, 한 Gfm github에서 언급하였던 해당 논문의 (주관적) 평가를 공유해드리며 이번 주 오마카세 글을 마무리하도록 하겠습니다.

💡

This paper shows a very simple trick can achieve promising performance to deal with the oversmoothing of transformers

Given the self-attention matrix A, view it as the adjacency matrix of a graph, inject higher-order information A^k into the self-attention matrix, and approximate it with Taylor expansion.

The detailed explanation needs further investigation.

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

정이태

이번주 오마카세에서는 최근 컬리에서 세미나한 내용을 공유드리려고 해요. 세미나 대상은 데이터서비스개발팀 및 검색추천개발팀 였었는데요.

팀 명에서 느껴지다시피 데이터와 검색 추천 그리고 비즈니스는 뗄레야 뗄 수 없을만큼 연관성이 큰 팀이였기에 어떻게하면 컬리에서 그래프를 잘 활용하실 수 있게끔 도와드릴 수 있을까 라는 고민을 시작으로 자료를 만들게 되었어요.

자료는 크게 1. Graph Understanding , 2. Graph Use Case , 3. GNN+LLM(GFM) 세 섹션으로 구성되어 있어요. 이커머스 분야에서 그래프를 정말 실용적이면서 트렌디하게 쓰려면 어떻게 할 지를 녹여내었다 라고 봐주시면 될 거 같아요.

그래프 모델링을 위해 그래프 종류 , 그래프를 담고 표현하는 방식에 대한 선행이 필요하기에 그 부분을 언급했구요. 그래프에 대한 이해도가 올라가게 되면 이를 어떻게 사용하면 좋을지 Linkedin 메타 데이터 관리 아키텍쳐 설명과 Graph Recommender System 두 부분에 대해 이야기했어요.

E-commerce 업종 특성상 유저들의 트렌드 템포가 상당히 빠르고, 유저들의 니즈를 만족하기 위해 상품들의 freshness와 검색 엔진의 성능이 중요할텐데 , 이 부분을 '상품 메타'가 많이 관여할 것이라는 생각 때문이였죠.

또한, 유저의 cold start 문제 그리고 co-behavior를 추출하기 위해 필연적으로 발생하는 JOIN 연산을 효율적으로 하는 그래프 본질적인 특성 관점에서 Graph Recommender system에 대해서도 이야기했어요.

GNN + LLM 세션에서는 LLM과 Graph 간의 관계에 대해 애매모호할 수 있을텐데, 이때 KDD24'의 tutorial 자료 중 정말 실무에 활용할 수 있는 GNN as prefix 와 LLM only 두 부분을 언급드리며, 만약 컬리에서 그래프를 구축한다면? 이라는 포인트도 이야기 드렸네요.

마지막으로는, 실제 유사한 산업 그리고 회사인 GS SHOP에서 최근 Bedrock을 활용해 검색엔진 성능 개선을 한 사례가 있어서 이 부분도 자료에 첨부하여 GS SHOP 개선 방식을 컬리에서 적용한다면? 이라는 IF 라는 관점도 함께 전달 드렸어요.

또한, 가장 큰 E-commerce 회사라고 할 수 있는 아마존에서 Knowledge graph + LLM 을 이야기한 COSMO 아이디어도 리뷰하면서, 실제 Graph + LLM을 동작하기 위한 아키텍쳐 그리고 Business ROI까지 이야기하며 세미나를 마무리 했습니다.

올해 E-commerce 분들을 대상으로 개인 그래프 세미나를 하게 된 건 벌써 두 번째인데요. 그만큼 상품과 유저간 관계를 구축해 검색 엔진개선 더 나아가 매출 증대까지 관심이 많음을 느낄 수 있었는데, 이 니즈가 있으신 분들에게 자료가 전달되어 잘 쓰이면 좋겠다는 마음이 드네요.

마켓컬리 발표자료-240926

마켓컬리 발표자료-240926.pdf

6 MB

함께 보시면 좋을 자료