10월 1주차 그래프 오마카세

Preview

On the Connection Between MPNN and Graph Transformer

→ Graph transformer 의 Self-attention,Positional-encoding 을 대체하기 위해 MPNN에서 어떤 시도를 할 수 있을까요? Virtual node 를 통해 앞선 두가지 요소를 대체하기 위한 아이디어에 대해 알아봅니다.

EquiformerV2: Improved Equivariant Transformer for Scaling to Higher-Degree Representations

→ Euqiformer 모델에서 scalable 를 위해 개선한 모델 EquiformerV2, 어떤 요소들을 추가하면서 Scalable 이 가능해졌을까요?

Is Distance Matrix Enough for Geometric Deep Learning?

→ GDL(Geometric Deep Learning)은 단순 거리만을 표현하는것이 다가 아니라 사면체 간의 거리 및 각도 또한 고려해야하는 분야라고 할 수 있습니다. 비정형 데이터인 그래프 데이터의 특성인 만큼 이를 자유자재로 잘 적용하는것 또한 중요한데요. 본 논문에서는 이를 특정하여 어떻게 GNN 모델을 개선하는지에 대해 다룹니다.

On the Connection Between MPNN and Graph Transformer

[https://arxiv.org/pdf/2301.11956.pdf]

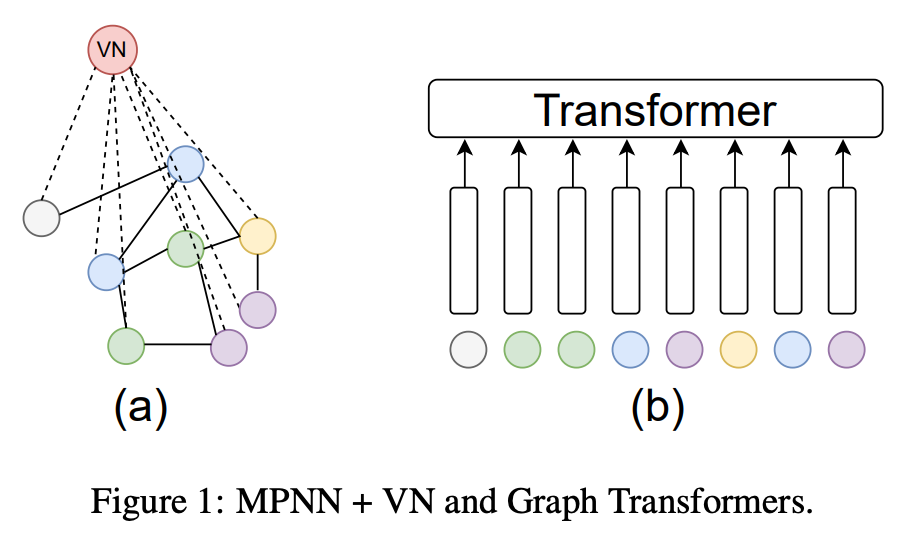
여러분들께서는 그래프 트랜스포머(GT)하면 어떤 키워드가 떠오르실까요? 저는 self-attention, position-encoding 그리고 expensive cost 이 3가지가 떠오르네요. 앞 2가지는 GT가 벡터공간상에서 표현력이 강하게 해주는 요소들이고, 마지막은 그 표현력만큼 발생하는 비용이 비쌈을 의미합니다.

이러한 GT의 비싼 비용을 문제로 정의하고, 비용을 절감하기위해 Performer/Linear transformer 와 같은 연산 효율화를 꾀한 모델들도 등장하곤 했습니다. 여러 시도들을 통해 결국 GT 계열은 OGB(open graph Benchmark) graph classification task 에서, LRGB(Long Range Graph Benchmark) 에서 강력한 베이스라인 모델로 거듭나고 또한 순위권을 위해 고려해야할 필수 모델 아키텍쳐로 자리매김했습니다.

이러한 GT 부흥 이면엔 MPNN(message passing neural network) 가 있습니다. MPNN 은 GT 도입전까지 graph classification에서 많은 인기를 얻고있던 모델이였습니다. 하지만, 그래프 토폴로지를 positional embedding 을 통해 더욱 정밀하게 표현할 수 있는 GT를 단순 message passing 을 통해 이겨낼 수 없어서인지 서서히 흐름이 MPNN에서 GT로 넘어갔습니다.

서론에 작성한 내용을 보시면 눈치채셨을수도 있습니다. 본 논문에서는 MPNN + α 를 통해 GT 보다 더 좋은 아키텍쳐를 만들어본다 가 핵심인 내용입니다. 여기에서 α 는 VN(virtual node)라는 요소인데, 해석 그대로 주어진 그래프에 가상의 노드 하나를 추가합니다. 이때, 가상의 노드는 주어진 그래프와 모두 연결되어 있는 그래프입니다. 이를 통해, MP(message passing)이 진행될때마다 노드의 정보들이 VN 으로 모여지고 분배되기에 global 정보를 고루 전달가능하다는 점이 VN 의 장점이자 기능이라 할 수 있습니다.

그럼, VN 이 GT 의 positional embedding 역할을 대체한다하면, GT의 또다른 장점인 self-attention은 무엇으로 대체했을까요? 바로 이종 그래프(heterogeneous graph) 형태를 차용하여 이를 대체했는데요. VN 과 GN(graph node) 가 각각 다른 노드 라벨으로 간주하여 1)VN-VN 2)VN-GN 3)GN-GN 3가지 경우를 활용하여 그를 대체합니다. 이 self-attention을 graph modeling 으로 대체하려고 하는 아이디어 부분이 저는 꽤나 흥미로웠었습니다.

이 각각의 경우를 모두 온전하게 보전하기 위해서는 결국 permutation invariant 가 중요한 요소일텐데요. 여기에서 permutation invariant 란 순서불변성을 의미합니다. 동일 노드들이 들어갔다하더라도, 순서가 변하면 아웃풋이 달라질 수 있는 경우가 발생하는데요. 이를 방지하기위해, 저자는 DeepSets이라는 알고리즘을 추가로 적용합니다.

실험 결과들이 굉장히 흥미롭습니다. 단순하게 VN을 추가하는것만으로도 성능을 향상시킬수 있다는 결과들이 보입니다. 핵심적인 내용만을 담기위해 부수적인 요소들을 언급하지 않았지만, 본 아이디어를 적용하기 위해 여러 가정들을 전제로 식을 풀어놓은 부분도 존재합니다. 디테일이 궁금하신분들은 논문을 살펴보시기를 추천합니다.

EquiformerV2: Improved Equivariant Transformer for Scaling to Higher-Degree Representations

[https://arxiv.org/pdf/2306.12059.pdf]

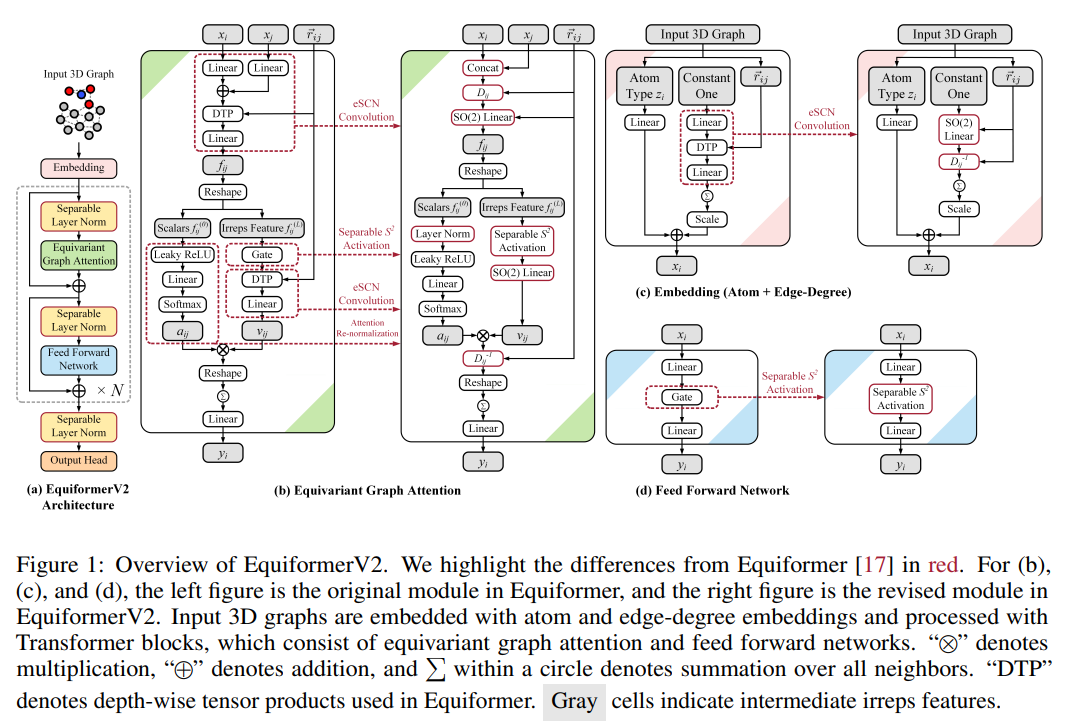
현대 입자 물리학 관점으로 트랜스포머를 개선한 아이디어입니다. Euquiformer 라는 구조에서 high-degree 정보를 반영하기에 계산복잡도가 크기에 그간 low-degree 정보만을 활용했다는걸 한계점으로 지적하고 이를 극복하기 위해 1.attention re-normalization, 2.separable S^2 activation 그리고 3.separable layer normalization 3가지 요소를 도입합니다.

기존 모델인 equiformer 에서 자주 언급되는 개념이 있습니다. 바로, irreps(irreducible representations) 입니다. 분자 구조마다 접촉 각도 , 떨어진 거리 등 기하학적 관점이 중요하게 여겨지는데, 등변성(equivalent)을 잘 보존하여 벡터상에 잘 표현하는게 핵심인데요. 이 때 활용하는 개념이 바로 irreps 입니다. 더욱 디테일하게 그 특성들을 보존하여 표현하기 위해서는 더더욱 많은 연산이 필요할텐데요. transformer 의 강점을 보존한채 scalable 아키텍쳐를 위해 어떤 시도들을 했는지와 그에 따라 어떤 결과가 나왔는지가 본 논문의 재미 포인트입니다.

Is Distance Matrix Enough for Geometric Deep Learning?

[https://arxiv.org/pdf/2302.05743.pdf]

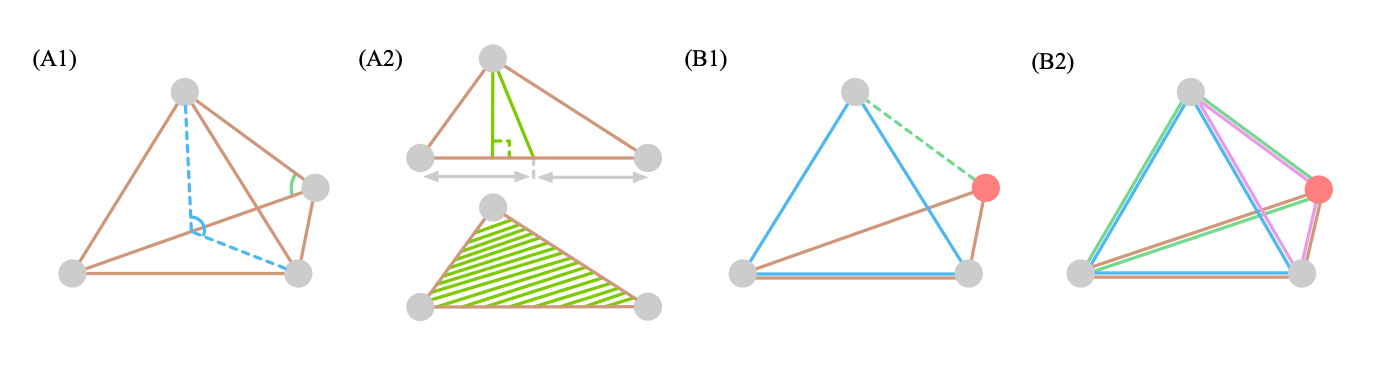
거리 그래프(Distance graph) 와 기하 그래프(Geometric graph) 의 차이점을 알고 계실까요? 명시적인 좌표가 그래프 특성에 담겨있는지 아닌지를 기준으로 나뉜다고 합니다. 그래프가 유용한 분야가 몇몇 있습니다. 그 중에서 신약개발, 소셜네트워크는 데이터 그 자체가 노드,엣지로 구성되어 있기에 별도의 그래프 모델링이 필요없이 그 자체의 데이터만을 잘 표현하는게 핵심이라 할 수 있습니다. 그렇기에 데이터 그 자체의 특성들 중 어떤 특성에 집중하여 표현할지에 따라 다양한 모델들이 개발되곤 하는데요. 오늘은 그 중 3D 공간 특성에 집중하여 표현하고자 하는 모델에 대해 알아봅니다.

그래프는 노드 와 엣지의 연결을 통해 완성되는 기하학적 도형에 공간 정보를 반영할 수 있다는 장점 덕분에 TDA(topological data analysis)에서도 많이 활용되고 있습니다. 여기에서 기하학적 공간에서도 차원을 거듭할 수록 그 표현력이 더해지는데요. 저희가 알고 있는 high-order 관점과는 약간 다르게 3D graph 에서 high-order는 각각 distance(2-order), angles (3-order) and dihedral angles (4-order) 라고 합니다.

그럼 이 정보들을 어떻게 벡터 공간상에서 표현할까요? graph isomorphism checking 할 때 베이스라인으로 쓰이는 WL algorithm 를 통해 표현합니다. WL algorithm은 그래프 동형사상을 점검하여 주어진 그래프와 비교하는 그래프를 구분하는 목적으로 주로 활용되어 왔습니다. 그간 1-order graph 에 대해서는 잘 작동하였지만, 고차원 공간 정보(2,3,4)를 반영하는데 있어, isomorphic type relabeling 한계가 있었습니다. 본 논문에서는 이를, k-FWL 측면으로 접근하여 그 한계를 극복해보고자 합니다. 간단하게 말하면 label type 을 다양하게 반영할 수 있는 Tuple trick 을 활용한다 라고 생각하시면 되겠습니다.

추가로 이를 어떻게 효율적으로 반복갱신하는 GNN 아키텍쳐를 만들 수 있을지에 대해서도 차근차근 GNN 핵심 스텝마다 친절하게 설명되어 있습니다. 어떻게 공간정보를 효율적으로 반영할지에 대한 고민이 있으셨던 분들에게 많은 도움이 될 거라 생각됩니다.