10월 2주차 그래프 오마카세

Preview
How Transitive Are Real-World Group Interactions? - Measurement and Reproduction
→ 그래프 지표 중 하나인 전이성(Transitivity), Hypergraph 에서는 어떻게 측정되며 생성모델에서는 어느 측면으로 접근할 수 있을까요?
A*Net: A Scalable Path-based Reasoning Approach for Knowledge Graphs
→KG Reasoning , 안그래도 비용이 많이 드는 알고리즘인 최단거리탐색 알고리즘을 지식그래프에 적용을 한다? A* 알고리즘을 지식그래프에 적용하여 scalability 문제를 해결해보고자 합니다.
Topological representation learning for e-commerce shopping behaviors
→ 고객의 쇼핑 경로를 그래프 형태로 변경하여 고객 세그먼트를 한다? 이상적이지만 현실성이 없었던 시나리오를 아마존에서 해냅니다. 특히 토폴로지 유사도를 도출하는 식이 굉장히 재밌습니다. 어떻게 경로간 유사도를 비교하는 인코더를 구현할까요?
How Transitive Are Real-World Group Interactions? - Measurement and Reproduction
[https://arxiv.org/pdf/2306.02358.pdf]
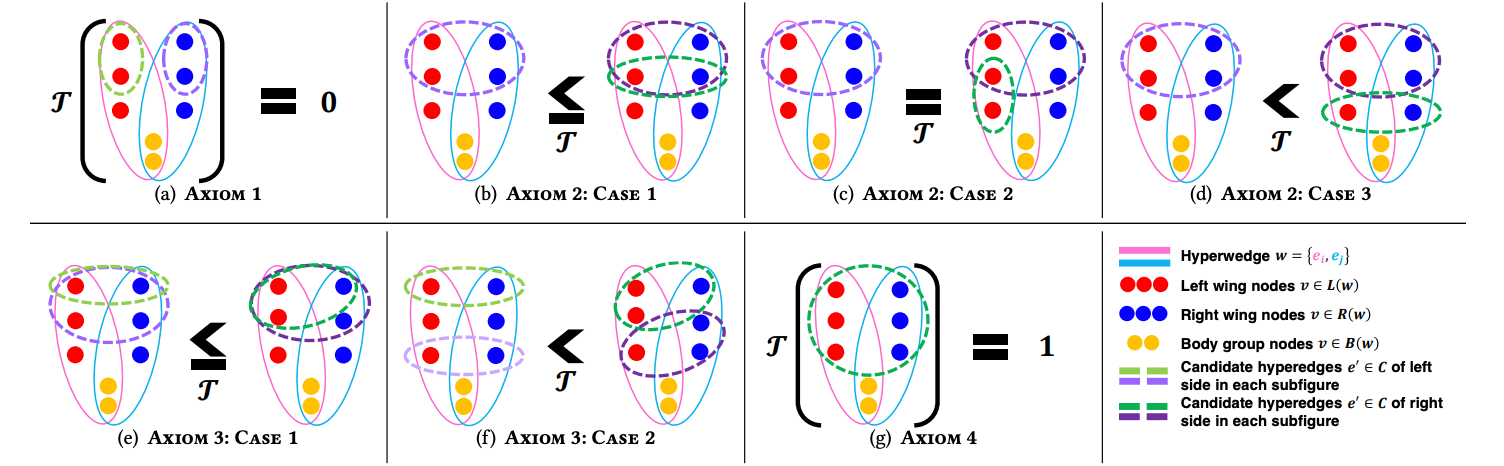
생성 모델의 목적 중 하나를 말해보자면, 현실 세계에서 있을법한 데이터를 과거의 데이터에 기반해 생성해내는것이라 생각합니다. 오늘은 저희가 친숙한 생성 모델 ChatGPT와 같은 텍스트 생성 모델과는 다른 그래프 생성 모델에 대해 알아봅니다. 그중에서도 특별한 하이퍼그래프 생성모델입니다. 그래프와 하이퍼 그래프의 차이점에 대해 익숙치 않은 분들이 계실꺼라 생각되어, 한줄로 간단히 요약해보자면 그래프는 ‘노드 쌍’ 에 대해 엣지로 연결된 그래프라고 한다면, 하이퍼 그래프는 ‘노드 그룹’에 대해 하이퍼엣지로 연결된 그래프라고 할 수 있습니다. ‘쌍’인 1:1 관계에 비해 ‘그룹’인 1:N을 다루기에, 그룹 상호작용을 관리하고 분석하는데 유용한 데이터 구조라고 할 수 있습니다.
본 논문에서는 하이퍼 그래프를 말하기 전 ,전이성(transitivity)에 대해 이야기합니다. 전이성이라함은 노드가 직접적인 연결이 되어있지 않더라도, 간접적인 연결을 통해 특정 노드들과 연결될 가능성을 의미합니다. 그래프 측면으로는 이게 직관적으로 떠오르지만, 하이퍼 그래프에서 전이성은 직관적으로 떠오르지가 않습니다. 바로 다양한 그룹들이 간접적으로 연결된다하면 고려해야할 경우의수가 굉장히 많기 때문인데요. 본 논문에서는 그 고려해야할 경우의수를 몇가지로 추려서 전이성을 측정하는 지표로 활용합니다.
여기에서 뜬금없이 지표가 왜 나오는지에 대해 의아하실 분들이 계실텐데요. 앞서 언급드린 ‘생성 모델’의 목적은 바로 현실 세계에 근접한 데이터를 생성하는것입니다. 본 논문의 목적은 하이퍼 그래프 생성 모델을 제안하는것이구요. 그렇기에, 현실 세계에 근접한지에 대해 측정하기 위해 지표가 필요합니다. 그 지표에 대한 기준이 바로 앞서 언급한 경우의수라 할 수 있습니다. 쉽게 말하자면, 지표를 설계하고 현실 세계 데이터와 생성해낸 데이터의 지표차가 적을수록 우수한 성능을 지닌 생성 모델이라 할 수 있습니다.
본 논문에서는 지표들에 따라 나온 결과치를 해석합니다. Observation 이란 부분에 그 해석들이 담겨있습니다. 해석들이 매우 통찰력있습니다. 결과 모두 어림짐작했으나, 수치로는 해석하기에 애매했던 부분들을 시원하게 긁어주는 해석들이기 때문인데요. 만일 하이퍼 그래프를 연구나 현업에서 적용하시는 분이시라면 이 부분을 꼭 보시는걸 추천드립니다. 생성모델을 직접 활용하지 않더라도, 가지고 계신 데이터의 통계를 추출하여 해석하실때 많은 도움이 될거라 생각되기 때문입니다.
추가로, 생성모델이 타 하이퍼그래프 생성모델 대비 성능을 높일 수 있는 이유로 커뮤니티 , 위계 두 가지를 꼽을수있습니다. 이를 어떻게 설계했는지 그리고 설계하면서 발생하는 연산 증폭 문제를 어떻게 접근하고 해결했는지를 보시는 것도 본 논문의 재미 중 하나라고 할 수 있습니다.
A*Net: A Scalable Path-based Reasoning Approach for Knowledge Graphs
[https://arxiv.org/pdf/2206.04798.pdf]
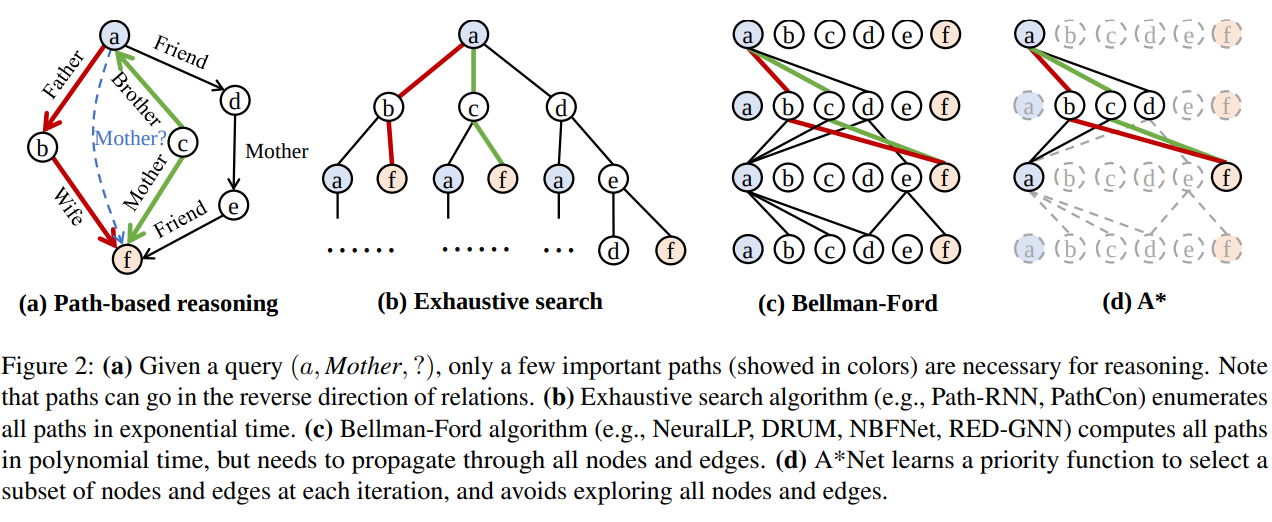
Knowledge Graph Reasoning , 대형언어모델 환각현상의 여러 대안 중 하나입니다. 지식그래프 노드간 경로를 탐색하며 답변에 도움이 될만한 경로를 추출하여 답변의 근거로 제시하는거죠. 설계된 지식그래프는 사실 및 지식을 그래프 형태로 변환한 데이터이기에 경로 자체가 현존하는 사실입니다. 다시말해, 답변에 대한 근거를 데이터에 기반하여 제시한다는게 KGR의 가장 큰 매력입니다. 하지만 여기에도 문제들이 존재합니다.
첫 번째는 답변과 관련된 경로를 어떻게 추출할지, 그리고 추출된 경로가 많은 경우 어떤 경로를 효율적으로 제시해야 하는지에 대한 문제입니다. 두 번째는 만일 답변과 관련된 지식이 데이터로 있다한들 두 노드(경로에 연관되어 있는 노드) 사이에 다른 관계나 노드가 담겨있으면 질의에 포함되지 않기에, 이를 생략하여 경로에 포함치않고 답변으로 내놓게 되는 문제입니다. 다시말해서, 놓칠 경우가 존재한다는거죠. 앞서 언급드린 두가지 문제 1. 경로 중요도 산출 2. 답변에 연관되어 있으나 중간 경유지가 없는 경우를 보완하기 위해 경로 추가 탐색 을 해결하기 위해 본 알고리즘을 고안했습니다.
SP(Shortest Path)알고리즘으로 많이 알려져있는 Bellman Ford 알고리즘을 보완하여 A* 알고리즘을 활용합니다. 여기에서 중요한점은 기존 SP 에서 적용하던 그래프 데이터들은 동종 그래프 형태였으나, 본 논문에서는 지식 그래프 형태에 적용한다는 점입니다. 그렇기에, 이종그래프에서 SP를 연산해야하기에 복잡도와 연산량이 기존 동종그래프 대비 상당합니다. 이를, 어떻게 효율적으로 처리하는지에 대해 보는것도 본 논문의 재미 포인트 중 하나라고 할 수 있습니다.
논문에서 주장하는 알고리즘은 SP 를 찾기위해 거리 함수와 휴리스틱 함수를 활용합니다. 거리 함수는 현재 노드와 목적 노드간의 거리를 측정하는 함수입니다. SP 알고리즘은 NP-hard task 에도 속해있습니다. 그래서 주어진 경우에서 최적의 정답을 도출하는게 핵심이기에 어떻게 최적의 정답을 도출하는지가 관건이라 할 수 있는데요. 여기에서는 휴리스틱 함수를 활용합니다. 논문에서는 이를 , Neural Priority Function 라고 부릅니다. 간단하게 말씀드리자면 path 마다 weight 를 설정하여 iterative traversal 하며 나온 값들을 종합한다 로 이해하셔도 무방할 거 같습니다. 이외에도, 여기에서 ground truth 가 없는 경우 negative sampling 을 어떻게 셋업하는지 등의 여러 시행착오들이 존재하는데 이를 해결하는 과정이 매우 흥미롭습니다. SP 알고리즘 그리고 reasoning 에 대해 한번쯤은 논문을 읽어보셨거나 공부하셨던 분들을 수월하게 읽을 수 있게끔 설명이 잘 되어 있습니다.
주목할만한점은, 여타 지식그래프 임베딩 혹은 GNN 대비 성능이 좋았다는 점인데요. 이를 다르게 해석해보면 결국 reasoning 에서 topology 가 역시 중요하다 라고 볼 수 있겠습니다.
Topological representation learning for e-commerce shopping behaviors
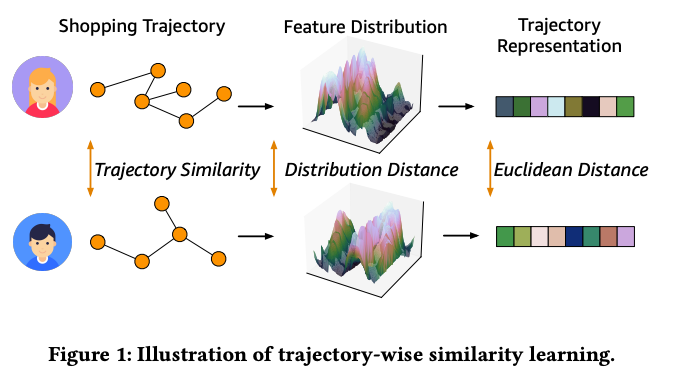
늘 고민했던 부분을 아마존에서 논문으로 시원하게 해결해주네요. 사용자의 쇼핑 행태를 그래프로 표현해 이를 기반으로 고객 세그먼트 , 쇼핑 마지막에 뭘 살지에 대해 어떻게 그래프로 추론할지에 대해 이야기합니다. 그래프 임베딩은 다들 경험하셨겠으나, 분포 관련으로 접근한점이 저는 매우 인상깊었습니다. 이전에 동일하게 그래프 모델링하고 서브그래프 임베딩(graph2vec)을 활용해 유저 이상행위 탐지를 주제로 사이드 프로젝트를 진행했던 기억이 떠오르네요. 일 단위의 임베딩값의 차이가 크다면 새로운 행위가 발생했다라고 가정하고 결과를 분석하니 흥미로운 결과가 몇몇 보였습니다. 단순하게 ‘차이’에 집중했었는데 여기에서는 분포 차이에 대해 더욱 세밀하게 접근했기 때문에 인상깊었습니다.
Topology Semantic 과 Topology Similarity 를 모두 반영한다고 보시면 될텐데요. 여기에서 Toplogy 유사도를 비교하기 위해서는 분포간의 차이를 비교해야합니다. 이를 위해 Optimal Transport Theory 와 Wasserstein distance 를 활용합니다. 여기에서 분포를 측정하고 측정한 분포를 관리하여 유사도를 어떻게 추출하는지 그리고 여기에서 최적화를 어떻게할건지에 대해 위에 언급한 두 가지 개념을 조화롭게 활용하는데 이부분이 굉장히 재밌습니다.
Ablation study 에서는 위 요소들을 w/o 에따라 결과가 어떻게 바뀌는지에 대해서도 언급하는데요. 주목할점은 KE(feature)대비 TSE(similarity)의 하락폭이 크다는 점입니다. 다시말해서, 토폴로지가 중요함을 실험을 통해 간접적으로 확인할 수 있는 재밌는 실험 결과를 발견할 수 있습니다.
주방장 개인적으로 굉장히 관심이 많았던 부분을 다룬 논문이라 싱글벙글하면서 읽었습니다. 매번 클라이언트와 만나서 이야기할때, 고민이였던 부분인 1. 타 회사에서 활용한다고 제시할 수 있는 레퍼런스 추가 , 2. topology similarity 를 path similarity 로만 접근했던 저에게 시야를 넓혀준 논문이기에 그랬습니다. 아마 저와 비슷한 고민을 하고 계신분(customer 360 + graph)이라면 많은 도움이 될 논문이라 생각하기에 추천드립니다!
