10월 3주차 그래프 오마카세

A Complete Expressiveness Hierarchy for Subgraph GNNs via Subgraph Weisfeiler-Lehman Tests
[https://arxiv.org/pdf/2302.07090.pdf]
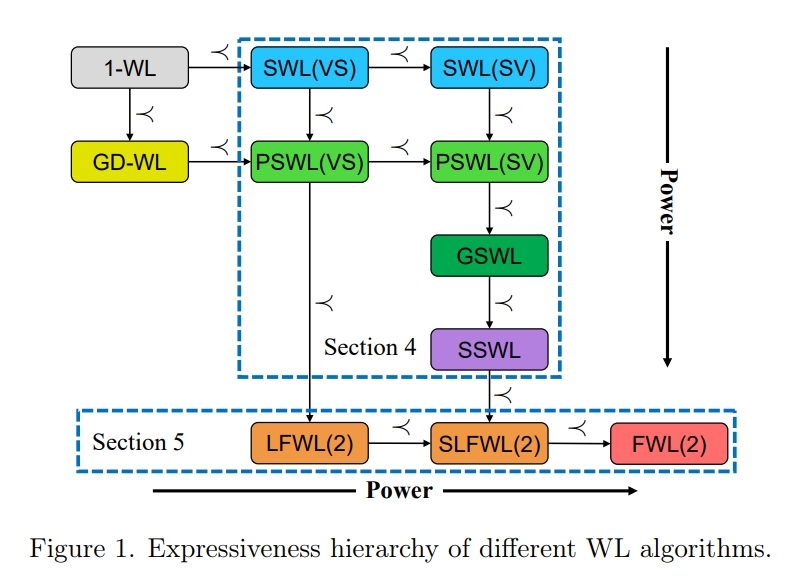
Expressive power, 그래프 데이터의 장단점을 논할 때 항상 강조되는 요소입니다. 노드 수와 엣지 수가 동일한 그래프라 하더라도, 그래프 내의 노드 연결 방식에 따라 다른 그래프로 구분됩니다. 따라서 '어떻게 연결'되는지를 이해하고 이를 숫자로 표현하는 것이 Expressive power의 핵심입니다. 이는 주로 동형사상(isomorphism test)을 통해 성능을 평가합니다. 모든 경우의 수를 측정하고 각각에 대한 고윳값을 찾아서 모든 그래프를 변환하는 것이 이상적일 수 있지만, 실제로는 한정된 자원으로 최고의 효율성을 내야하기 때문에 장밋빛 상황은 드물게 발생합니다. 따라서 효율성을 추출하기 위한 여러 시도가 진행 중입니다. 이 논문은 이러한 시도 중에서 '계층'에 중점을 두고 Expressive power에 접근합니다.
1.Graph generation policy, 2. Message-passing aggregation schema, 3. Final pooling schema는 Subgraph GNN 알고리즘의 작동 프로세스입니다. 그래프를 추출할 때, 서브그래프를 모두 가져올지, 특정 노드를 제외하고 가져올지, 특정 hop 이상의 에고네트워크를 가져올지 등 서브그래프를 가져오는 방법은 다양합니다. 또한, 추출된 서브그래프 간에 연결된 노드만 정보를 교환할지, 특정 노드만 정보를 교환할지, 전체 서브그래프를 모두 통합하여 정보를 교환할지, 집계에 대한 선택지도 다양합니다. 어떤 것이 적합한 상황인지 결정하기 위해서는 다양한 시나리오와 실험이 필요합니다. 이러한 복잡한 과정을 거치고 나면 드디어 저희가 활용할 수 있게끔 데이터가 숫자로 표현됩니다.
많은 경우의 수 중에서 어떤 것이 합리적이고 효율적인지를 결정하는 것은 복잡한 문제입니다. 논문 저자들도 이 문제를 경험하였기에 문제로 정의하고, 해결하려고 본 아이디어를 생각해냈습니다. 이 논문에서는 서브그래프간 특성을 도출하는 과정속에 계층이라는 요소를 도입해 성능을 향상시킵니다. 예를 들어, 로컬 집계(local aggregation)가 글로벌 집계(global aggregation)보다 성능이 우수하다면, 이를 논리적 관계식으로 적용하여 계층을 구분합니다. 이런 방식으로 성능에 따라 계층을 정의하면 여러 가지 클래스가 나타납니다. 이를 활용하여 동형사상을 검증합니다.
알고리즘 효용성을 검증하기위해 'pebbling game' 도구를 사용합니다. 알고리즘의 성능과 별개로, 이 도구가 어떻게 작동하는지에 대한 과정이 굉장히 흥미롭습니다. 이 도구는 조약돌(pebble)를 추가하거나 제거하면서(논문에서는 Spolier, Duplicator 플레이어 간의 상호작용을 통해 진행한다고 합니다) 다양한 시나리오를 생성하며 알고리즘들이 그것을 구분할 수 있는지를 검토합니다.
Subgraph GNN은 주로 생물학에서 분자 구조 분석과 추론에 활용되지만 그래프의 활용 가능성이 확장되며 금융, 제조 분야를 포함한 여러 분야에서 그 활용도가 높아질것으로 생각되기에, 서브그래프를 통해 가치를 도출하는데에 관심과 호기심을 가지신 분들에게 여러모로 많은 도움이 될거라 생각합니다.
From hypergraph energy functions to hypergraph-nueral-networks.
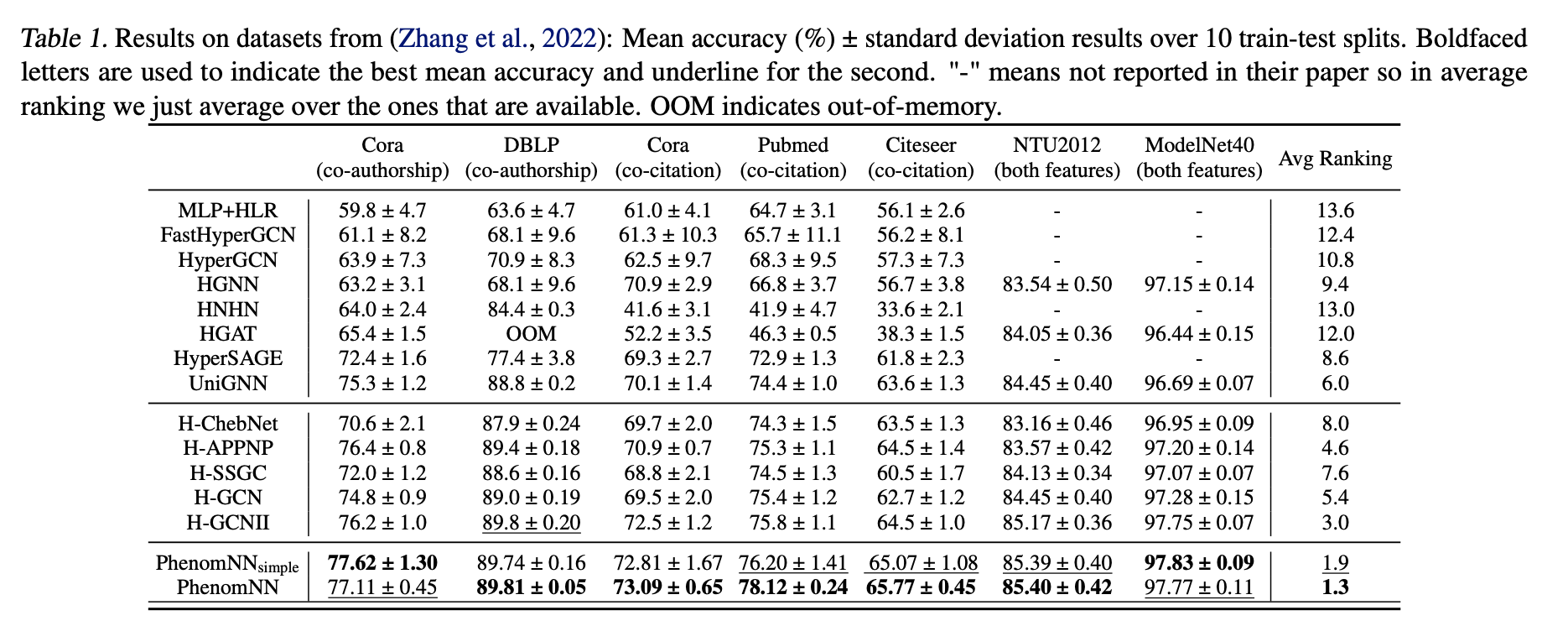
Energy function , 오랜만에 접하는 알고리즘입니다. 볼츠만 머신을 공부할 때 이후 간만에 보는거 같네요. 본 논문에서는 energy function의 explicit parameterized 특성을 활용합니다. 에너지를 효율적으로 최소화하는 과정에서 발생하는 이펙트를 노드 임베딩에 활용한다는게 논문의 골자입니다. Energy function을 활용해 hypergraph node classification task성능을 개선한다. 굉장히 말로는 쉬워보이지만,여러 복잡한 과정이 이 알고리즘을 이루고 있습니다.
하이퍼그래프에 적절한 Energy function 을 디자인 하는것부터 시작하여, Energy function 핵심인 regualzation 을 어떻게 설계하고 도출된 값을 바탕으로 어떻게 최적화하는지 등 흔히 저희가 생각하는 인공신경망을 처음부터 다시 설계한다 라고 보시면 되겠습니다. 특이하게도 본 논문에서는 만일 hyperedge의 feature가 없을때를 고려하여, star expansion 과 clique expansion을 언급합니다. graph ↔ hypergraph 를 변형하며 발생하는 정보들을 활용한다는게 핵심인데요. 이 과정 또한 굉장히 흥미롭게 서술되어 있기에 한 번 살펴보시는걸 추천드립니다!
CAN LLMS EFFECTIVELY LEVERAGE GRAPH STRUCTURAL INFORMATION: WHEN AND WHY
[https://arxiv.org/pdf/2309.16595.pdf]
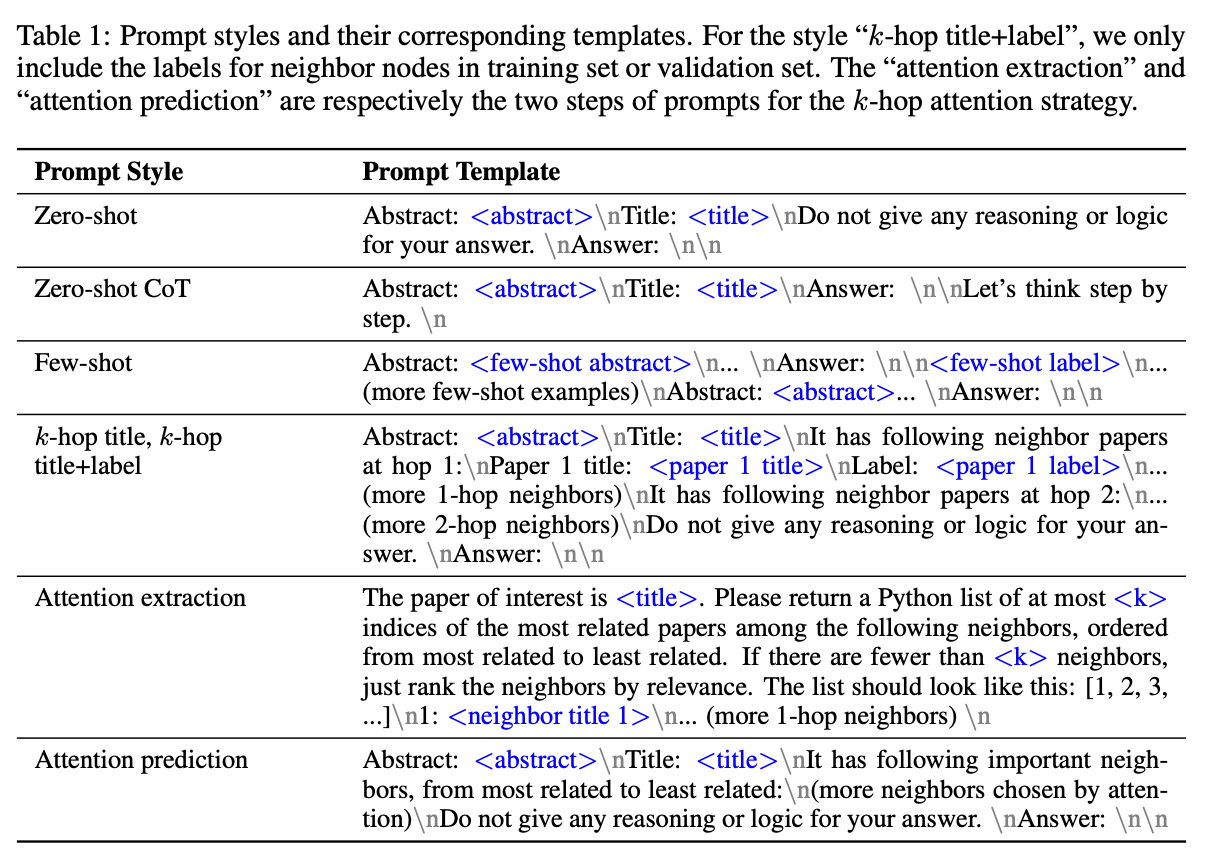
LLM, 요즘 LLM 모르면 간첩이라는 말이 나올만큼 인공지능 씬에서는 굉장히 뜨거운 감자인 주제입니다. 그래프 기술도 이 흐름에 맞춰 보완재로써 톡톡한 역할을 하고 있습니다. 주변에서 “왜 LLM에 그래프를 써야할까요?” , “LLM과 그래프요? 제가 그래프를 접목했을떄 별로 좋지 않던데요?” 등 차가운 시선을 받고 계시다면, 혹은 앞서 언급한 의문들처럼 의심하고 계시다면 본 논문이 그것에 대한 해답은 아니지만, 조금이나마 도움이 될 논문이라 생각합니다.
논문 제목에 나와있듯이, ‘왜?’,’언제?’ 라는 물음을 중점으로두고 논문이 작성되어 있습니다. Prompt styles 인 zero-shot, few-show, CoT 와 그래프 구조적 특성을 고려하여 토폴로지와 LLM을 결합한 것에 대한 호기심을 잘 풀어낸 논문이라 할 수 있습니다. 특히, 동종성(homophily)을 활용하는 측면이 감탄 그 자체였습니다. 마침, 그래프 딥러닝 오픈채팅방에서 프롬프트에게 link prediction 을 언급하여, RAG를 실험한 결과물을 본 후에 본 논문을 접했던터라 그래프 task를 프롬프트에 접목하여 진행한다면 더욱 굉장한 결과물이 나오지 않을까 하는 생각도 하게 되더군요.
LLM에 그래프가 도움이 된다는데, 그래서 구체적으로 어떻게 될까? 라는 막연한 의문에 대해 해답을 준 논문이기에 그래프에 트렌드를 접목하기 위해 공부중이신분들 특히나 추천드립니다. 또한, 산업계에서 환각현상 때문에 골치아프신분들에게도 추가적인 특성을 고려할 수 있는, 시야를 넓힐 수 있는 인사이트를 가져다주는 논문이라 생각하기에 또한 추천드립니다!
