25년 8월 2주차 그래프 오마카세

Graph Tensor Networks: An Intuitive Framework for Designing Large-Scale Neural Learning Systems on Multiple Domain

paper link : https://arxiv.org/abs/2303.13565

• 현재 토폴로지 신경망의 학습 메커니즘을 설계하는 과정에서 매우 중요한 텐서 연산에 대한 이해를 크게 도와준 논문 하나를 여러분들께 소개해드리려고 합니다. 그래프 구조를 활용하여 다양한 신경망의 텐서 연산 과정을 쉽게 이해할 수 있도록 잘 설명한 논문인만큼, 많은 도움이 되실 수 있을 것 같습니다.

• 보편적으로 딥러닝 모델들은 벡터, 행렬 사이의 곱셈 연산과 비선형 활성화 함수를 결합한 형태로 학습 패러다임이 구성됩니다. 의외로 단순한 연산들만으로도 다양한 입력 데이터들의 복잡한 패턴들을 이해할 수 있고, Regular & Irregular 도메인에서 여러 tasks를 잘 수행하는 것이 참 놀라운 것 같습니다. 이러한 학습 패러다임은 감사하게도 다앙한 딥러닝 라이브러리에서 쉽게 잘 구현되어 있습니다.
• 이미지에서 강력한 CNN, 시계열 데이터에 강력한 RNN, 그리고 그래프에 강력한 GNN 등, Inductive bias에 따라 선택되는 맞춤형 딥러닝 모델들이 잘 알려져 있습니다. 포괄적으로 텐서라는 개념을 사용하여 이들이 받는 입력 텐서 형태와 그에 맞는 텐서 연산들은 제각각 다릅니다.
  • 텐서는 벡터(1차 텐서)와 행렬(2차 텐서)을 다차원으로 일반화한 것입니다. 이러한 텐서 연산은 차원의 저주(Curse of Dimensionality)로 인한 고차 임베딩 공간의 병목 현상을 우회하고, 연산 비용을 데이터 차원에 대해 지수 함수에서 선형 함수로 줄일 수 있어서 낮은 복잡도로 대규모 데이터를 효율적으로 처리할 수 있다는 사실이 잘 알려져 있습니다.
• 실제 다양한 데이터는 복수의 도메인(e.g. 비디오 : 시&공간 / 사회 네트워크 : 텍스트 + 그래프 도메인 등..)이 혼합되어 있습니다. 이들을 표현하는 매우 고차원적인 입력 텐서를 고려한다면, 복잡한 표기법들과 그 연산 자체가 상당히 추상적이어서 직관적으로 이해하기 어렵습니다.
  • 소수의 연구들(대표적으로, "Tensorizing Neural Network") 에서는 Tensor Algebra를 바탕으로 근본적인 신경망의 텐서 연산을 이해하고 TTN & QTTN 등의 효율적인 텐서 분해 기법들도 같이 설명해주고 있습니다. 하지만 글로 이 내용들을 이해하기엔 머리가 상당히 아플 수 있습니다.
• 이러한 개념적 어려움을 해소하기 위해 양자 물리학(Quantum physics) 커뮤니티에서는 복잡한 텐서 연산을 수학적 그래프로 시각화하고 구현하는 '텐서 네트워크(TN)'라는 그래픽 접근 방식이 개발되었습니다. 이 TN 프레임워크는 대규모 다차원 연산을 간단한 그래픽으로 시각화하고 조작할 수 있게 하여 신경망 설계에 큰 이점을 제공할 수 있습니다.
• 해당 논문에서는 다양한 신경망 (e.g. DNN, CNN, GCN, Attention-based)의 학습 메커니즘을 그래프 기반 텐서 연산으로 해석하는 일반적인 프레임워크, Graph Tensor Network (GTN)을 소개합니다. 기존의 방식보다 상당히 직관적으로 쉽게 이해할 수 있으며, 모든 종류의 다양한 데이터 도메인의 데이터를 처리할 수 있을 만큼 충분히 유연함을 언급합니다.

• 기본 텐서 대수에 대한 모든 설명은 생략하고, 핵심 개념만 짚고 넘어가겠습니다.
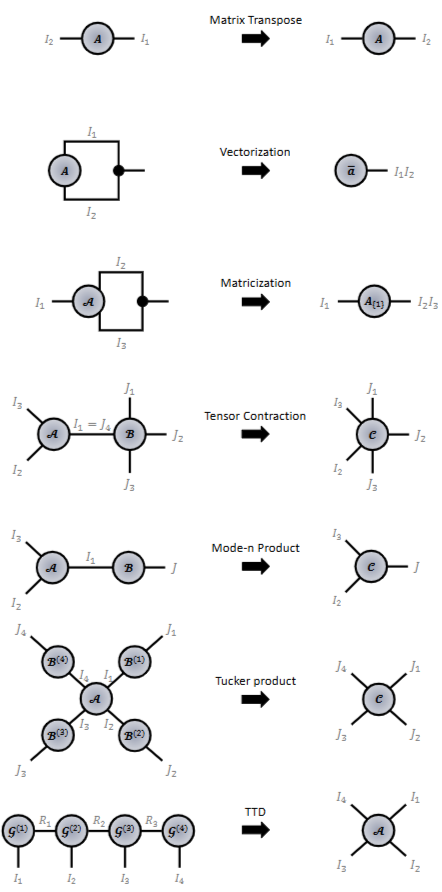
  • 벡터화 (Vectorization) : N(>1)차 텐서를 1차 텐서인 벡터로 변환하는 과정을 의미합니다. 각 모드(I1 x I2 > 1 x (I1 * I2) 의 곱셈을 통해 변환됩니다. 시각화는 논문을 참고해주세요.
  • 행렬화 (Matricization) : 마찬가지로 N(>2)차 텐서를 2차 텐서인 행렬로 변환하는 과정을 의미합니다. 하나의 모드를 제외난 나머지 모드의 곱셈으로 진행됩니다. 시각화는 논문을 참고해주세요.
  • 텐서 컨트렉션 (Tensor Contraction) : 2가지 종류의 모드(N개의 도메인 모드 & M개의 특징 모드; N x M 표기)를 갖는 텐서들 간의 곱셈으로 정의됩니다. `x_n^m' 로 표기됩니다.
    • 두 텐서 A^{I1 x...x In}, B^{J1 x...x Jm} 에 대하여 A x_n^m B는 A 텐서의 n번째 모드 I_n 와 B 텐서의 m번째 모드 J_m을 곱하여 (N+M-2)차원의 결과 텐서를 얻어내는 연산입니다. 여기에서 행렬 곱셈과 동일하게 곱해지는 모드의 크기는 반드시 I_n = J_m이어야 합니다.
    • 텐서 컨트렉션 연산은 항상 미분 가능하기 때문에 현재 다양한 대수 라이브러리에서 널리 사용되고 있습니다.
  • 모드-n 곱셈 (Mode-n Product) : N(>2)차원 텐서 A^{I1 x...x In}와 2차원 텐서 B^{J x In}에 대하여 A x_n² B 의 곱셈으로 정의됩니다. 즉, A의 n번째 모드와 (I_n) B의 2번째 모드 (I_n)에서 연산이 진행되며, 두 크기가 같다면 일반적인 행렬 곱셈과 동일합니다. (=BA_(n))
  • 터커 곱셈 (Tucker Product) : 모드-n 곱셈에서 하나의 2차원 텐서가 아닌 여러개의 2차원 텐서 {B⁽¹⁾,...,B^(N)}들과의 곱셈을 정의합니다. 모드-n 곱셈 방식을 그대로 가져와서, 각 B 행렬마다 동일한 모드의 A 텐서들과 여러번의 행렬곱셈 (=A x₁² B⁽¹⁾ ... x_n² B⁽ⁿ⁾)으로 진행됩니다. 시각화는 Fig 3을 참고해주시면 되겠습니다.
  • 텐서 분해 (Tensor-Train Decomposition, TTD) : 두 텐서 A, B의 곱셈으로 발생하는 막대한 연산코스트를 줄이기 위해, N개의 텐서 코어 (G)로 분해히여 근사화 기법으로 적용됩니다.
    • 기하급수적인 본래 텐서 공간복잡도를 선형 합으로 크게 줄일 수 있어 널리 활용되고 있으며, 2=I_n=J_n=R_n(특정 텐서의 랭크; 저차원 모드로 줄이는 스케일 팩터로 동작) 일때, 효율적인 압축을 의미하는 QTTN (Quantized TTD)을 만족할 수 있음이 증명되어져 있습니다.
  • 컨볼루션 텐서 (Convolution Tensor) : 컨볼루션 텐서 C^{I x I xP}는 희소 3차 텐서로써 해당 조건을 만족하는 인덱스(t)에만 1값이 채워지는 indicator 연산자입니다.
    • t_{i,(i+p-1)%I, p}를 만족하는 위치에만 1로 채워집니다. 여기에서 %기호는 (i+p-1)를 I로 나눈 나머지값을 반환하는 모듈러입니다.
    • 다음 컨볼루션 텐서를 이용한 입력 벡터 v와 컨볼루션 커널 k 간의 이산 컨볼루션은 다음과 같이 정의됩니다.
      • x * k = C x₂¹ v x₃¹ k = (C x₃¹ k = S) x ; 컨볼루션 텐서와 1차 텐서인 v, k 간의 모드-1 곱셈을 수행합니다. 여기에서 S^{I x I}는 입력 커널 x 상에서 커널 텐서 k를 순환시키는 역할을 수행합니다. CNN의 stride하며 컨볼루션 연산을 수행하는 것으로 바라볼 수 있습니다.
        • 순환 그래프의 관점에서, 다음 텐서 S는 GSO (Graph Shift Operator; 데이터 도메인에서 특정 도메인 (e.g. 스펙트럼 공간)으로 맵핑시키는 함수)의 인접 행렬 꼴로 표현되어집니다. 이로부터 그래프 컨볼루션으로 일반화 가능합니다.
      • 다음 컨볼루션 텐서는 실제로 QTTD 효율 압축을 만족함이 증명되어졌습니다.

• 다음 텐서 연산의 개념들을 바탕으로, 기존 딥러닝 모델들의 포워드 연산을 해석해볼 수 있겠습니다.

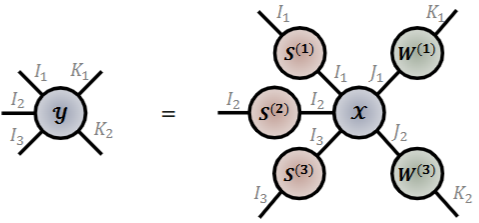
• 다음 그림은 (3 x 2 ; 3개의 도메인 모드와 2개의 특징 모드)차 입력 텐서 x로부터 출력 텐서 y를 얻어내는 과정을 그래픽으로 시각화하였습니다. 여기에서 터커 곱셈이 활용됩니다.
  • 하나의 입력 텐서 X의 3가지 도메인 모드(I_1,2,3)들에 대해서 3개의 GSO 행렬 S^(1),(2),(3)과 터커 곱셈을 수행하고, 특징 모드 (J_1,2)에 대해서 2개의 가중치 행렬 W^(1),(3)과 터커 곱셈을 수행합니다.
  • GSO, W 행렬을 2차 텐서로 바라보면, 다음 포워드 연산은 쉽게 모드-2 곱셈으로 변환될 수 있으며, X의 특정 모드에 대한 GSO 및 W 행렬 간 행렬곱셈으로 이해할 수 있겠습니다.
• DNN의 포워드 연산은 아래와 같이 나타낼 수 있습니다.

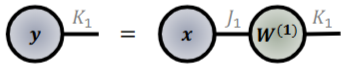
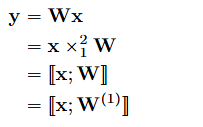
• (0 x 1 ; 1개의 특징 모드)차 입력 텐서 x와 2차 텐서인 가중치 행렬 W의 연산을 모드-1 곱셈으로 표현 가능합니다.
• 또한, 한 개의 입력 텐서와 한개의 행렬을 가지고와서 터커 곱셈으로도 표현할 수 있습니다.
• GCN의 업데이트 연산은 아래와 같이 나타낼 수 있습니다.

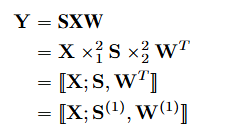
• 입력 텐서 X, 가중치 행렬 W, 그리고 GSO 행렬 S에 대하여, 모드-1,2 곱셈으로 표현할 수 있습니다.
• 또한 한 개의 입력 텐서와 두 개의 행렬을 가지고 와서 터커 곱셈으로도 표현할 수 있습니다.
• CNN의 컨볼루션 연산은 아래와 같이 나타낼 수 있습니다.

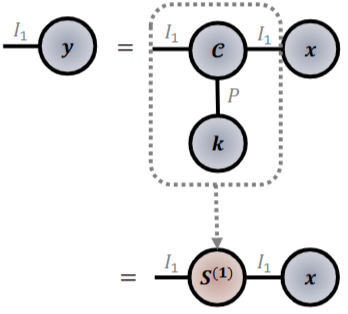
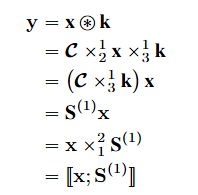
• 컨볼루션 텐서를 이용하여 진행되는 이산 컨볼루션 연산은 DNN과 동일하게 모드-1 곱셈 및 터커 곱셈으로 간단히 표현될 수 있습니다.
• 마지막 어텐션 연산에 대해서 아래와 같이 나타낼 수 있습니다.

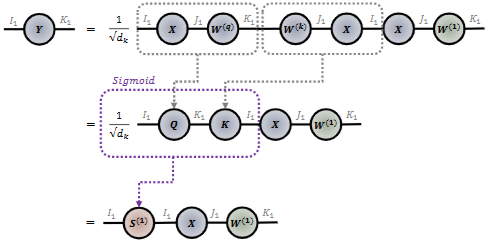
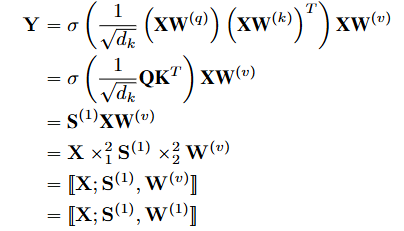
• 쿼리, 키 행렬에 대하여 모드-2 곱셈을 통해 GSO 행렬 S를 만들고, 모드-1 곱셈 및 밸류 행렬에 대하여 모드-2 곱셈을 적용하여 진행되는 것을 알 수 있습니다.
• 한 개의 입력 텐서 X에 대하여 2개의 행렬 GSO, W을 가지고 와서 터커 곱셈으로도 표현할 수 있습니다.

• 다양한 신경망 모델의 텐서 연산을 시각적으로 또는 직관적으로 표현 가능한 그래프 텐서 네트워크, GTN은 추가적으로 텐서화 트릭(Tensorization Trick)을 통한 압축 및 멀티 그래프 모델링 (Multi-Graph Modelling)을 통한 다중 도메인 데이터 처리가 가능합니다.

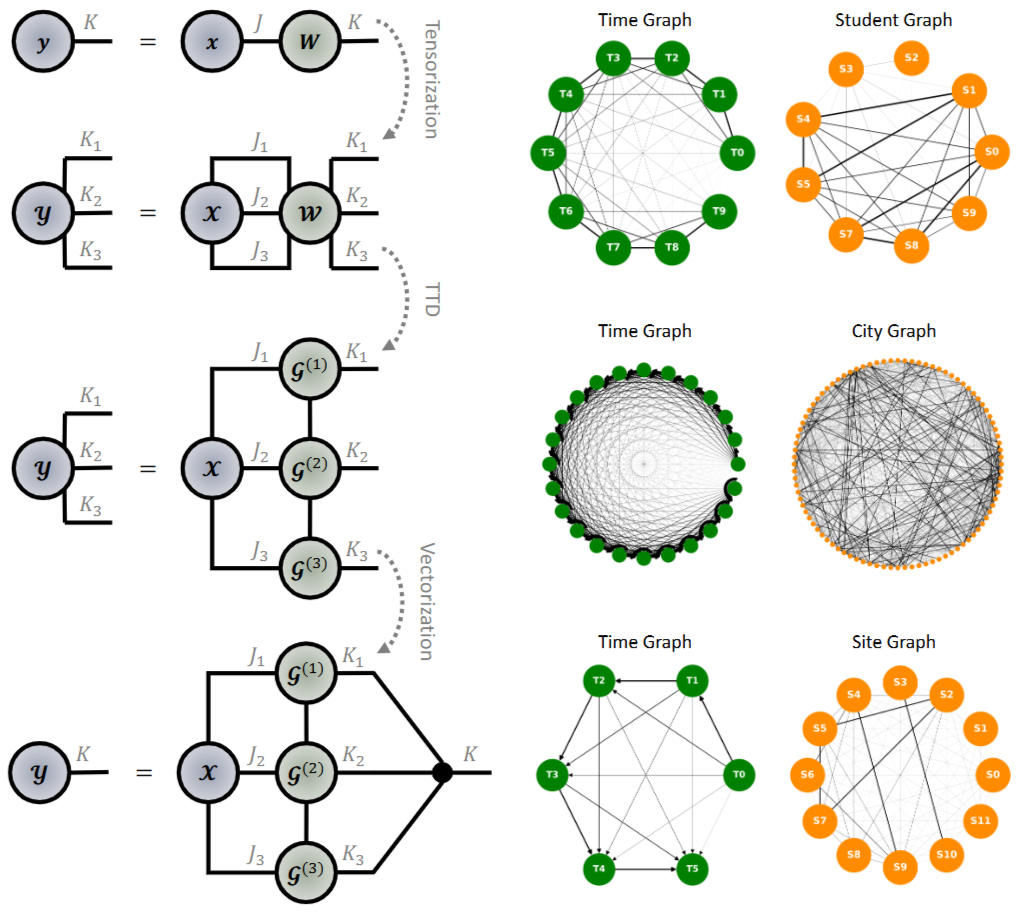
• 왼쪽 그림은 DNN의 연산 과정에서 가중치 행렬 W의 텐서화 트릭을 보여주어 연산 효율성을 극대화하는 과정을 시각화하고 있습니다.
  • 2차 텐서인 W^{J x K}를 (3 x 3)차 텐서 W^{(J1,2,3 x K1,2,3)}으로 텐서화한 후, 3가지 텐서 코어 G^(1),(2),(3)들로 분해하여 출력 벡터 y로 벡터화하는 여러 텐서 연산들의 조합을 보여줍니다.
  • 결과적으로 일반적인 DNN의 결과와 동일하지만, 연산 코스트 측면에서 크게 줄어들어 그 이점을 강조할 수 있음을 언급합니다.
• 오른쪽 그림은 다양한 다중 태스크 (EEG : 신호 & 그래프 도메인; 온도 예측 : 온도 & 시간 도메인; 등등)에서 표현된 GTN의 유연성을 보여줍니다. 즉, 기존 신경망들 (CNN, GNN, RNN..)들의 단일 도메인에 한정되어 적용되는 한계를 극복하는 사실을 언급합니다.

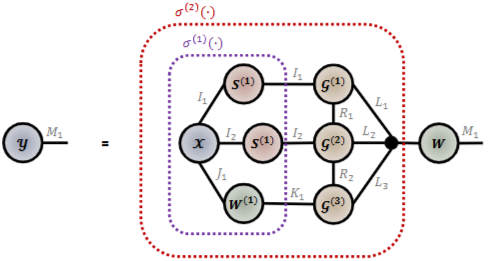
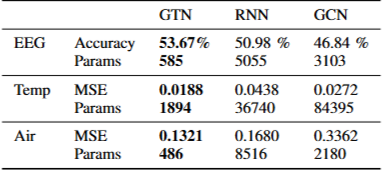
• 마지막으로 위 그림과 같이, 다양한 신경망의 텐서 연산을 일반화하여 그래프적으로 표현한 GTN 아키텍처를 다양한 실험환경에 적용하였을 때 향상된 성능 및 큰 연산 효율성 등을 확인할 수 있었음을 언급합니다.
  • 아키텍처 측면에서 크게 두가지 레이어로 구성되어 있습니다.
    • 첫번째 레이어에서는 (2 x 1)차 입력 텐서 X^{I1 x I2 x J1}에 대해서 도메인 모드에 대한 2가지 GSO, S⁽¹⁾,와 특징 모드에 대한 1가지 가중치 행렬, W,를 가지고 터커 곱셈을 형성합니다.
    • 두번째 레이어에서는 연산량을 줄이기 위해 텐서화 트릭을 활용하여 TTN 및 벡터화 기법이 적용되었습니다.
    • 활성화 함수를 적용하여 비선형성을 부여하였습니다. Remark 1에서 언급되었듯이, 모든 텐서 연산들은 활성화 함수에 독립적으로 적용될 수 있기 때문에 전체적인 그래프 토폴로지에는 큰 변화가 없음을 장담할 수 있습니다.

• 토폴로지 딥러닝에서 고차 텐서들을 입력으로 받는 경우가 많기 때문에, 기존 신경망들의 텐서 연산들부터 하나씩 정확하게 짚는 것이 중요하다고 생각하여 관련 공부를 하고 있습니다. 개인적으로 해당 논문이 가장 이해하기 쉽고 그래프를 통한 직관적인 시각화를 제공하고 있어 많은 도움을 받았던 것 같습니다.
• 위 내용을 한 문장으로 요약하면 다음과 같습니다.
  • 다양한 신경망들의 내부적인 텐서 연산 기반 학습 메커니즘을 직관적으로 그리고 시각적으로 잘 표현하여 이해를 돕고, 트릭 기법 및 다중 도메인으로 적용 가능한 유연한 프레임워크 GTN을 제안하였습니다.

[Contact Info]

Gmail: jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn