24년 9월 2주차 그래프 오마카세

Convolutional Learning on Simplicial Complexes

paper link : https://arxiv.org/abs/2301.11163

배지훈

• 그래프 상의 pairwise relation 관계를 인코딩하는 것에 그치지 않고, 노드 및 엣지로 표현될 수 있는 higher-order한 structural information 까지 한번에 인코딩할 수 있는 Simplicial complex에 대해 집중적으로 오마카세에서 다루어보고 있습니다.
• Real-world에서는 단순한 관계성만 존재하는 것이 아니라 여러가지 복합적인 관계 요소들이 얽혀있으며, 이들을 잘 풀어헤쳐서 독립적으로 분석 및 특징을 잘 추출할 수 있는 방법이 있으면 더욱 효과적일 것 같습니다. 하지만 단순한 아이디어에 비해 실제로 다음을 잘 표현할 수 있는 임베딩 벡터로 표현하는 것부터 신경망 모델을 구축하여 한번에 이들을 학습하는 알고리즘을 구현하는 것은 꽤나 어려운 일입니다.
• 2020년 이래로, Topological deep learning의 발전이 눈부시게 빠르게 이루어지고 있으며 특히 Simplicial complex라는 복합체 상에서 위에서 언급한 다양한 구조 요소들을 학습할 수 있는 모델 설계에 많은 노력을 하고 있습니다. 다음은 이전 오마카세 글의 깃허브 링크 주소를 확인해주세요.
  • CNN의 컨볼루션 연산, 다음을 비유클리드 데이터로 확장하여 컨볼루션 학습이 가능해진 GCNs의 발전에 영감을 받아, 컨볼루션 커널 설계 및 메세지 전달 메커니즘을 활용한 재밌는 토폴로지 컨볼루션 연산 방법들이 많이 나오고 있습니다.
  • 다음 방법들을 최대한 오마카세에 잘 녹여 담아, 독자 여러분들께 새로운 시각에서 활용하시고자 하는 데이터 혹은 해결하고자 하는 문제에 확장된 방법론들을 제공해드리고자 하는 것이 저의 목표입니다 !
• 두서가 꽤나 길어졌습니다. 이번 주 오마카세는, 토폴로지 측면에서 higher-order networks 상에 존재하는 입력 신호들 상의 컨볼루션 연산을 수행할 수 있는 Simplicial Complex Convolutional Neural Netowkr (SCCNN) 모델을 설명해드리고자 합니다. 신호 관점에서 접근하는 방법론이다보니, 7월 3주차 ~ 8월 1주차까지 전달해드렸던 토폴로지 신호 처리 (TSP) 설명글을 참고하시면서 읽어주시면 받아 들이시는 데 어려움이 없지 않을까..라고 생각합니다.

• 8월 4주차에 전달해드렸던 SNNs을 기억해보시면, 결과적으로 정의한 Simplicial Convolution operation은 동일한 p차수의 co-chain simplex상에서 i차수 Hodge Laplacian (i번 거듭제곱 꼴) 및 가중치 행렬을 통해 수행되었습니다. 다음 컨볼루션을 다른 차수의 simplex 상에서 정의해볼 수 없을까요? 자연스러운 질문이 될 수 있습니다.
• 본 논문에서 저자들은 SNNs의 직접적인 Simplicial Adjacencies 뿐만 아니라, 신호적 측면에서 고차수의 Simplicial Adjacencies 및 inter-simplicial coupling 관계를 포괄적으로 포착할 수 있는 방법을 제시하고자 합니다. 즉, SNNs을 일반화할 수 있음을 보입니다. (Table 1 참고)

• 제안 모델 SCCNN의 핵심 아이디어는 Hodge Laplacian 행렬이 직접적으로 인코딩하는 Simplicial complex의 Face & Co-face 간의 인접성을 활용하는 것이며, 해당 표현정보로부터 반드시 고려해야 할 모델의 Permutation & Orientation Symmetry의 만족성과 그로부터 통합되는 학습의 Inductive biases를 입증합니다.
• 또한 스펙트럼 관점으로부터 어떻게 제안 모델 SCCNN이 주어진 데이터를 Regulate할 수 있는지, 마지막으로 Perturbation domain (e.g. Domain deformations)으로부터 Learning Stability를 만족하는지를 이론적으로 분석하여 상세하게 제시합니다.
• 최대한 복잡한 수학적 수식은 제외하고, 해당 논문에서 제공하는 (정말 쉽게 이해할 수 있는) Figure를 기반으로 설명해드릴 수 있도록 하겠습니다.

Simplicial Complex Convolutional Neural Networks (SCCNNs)

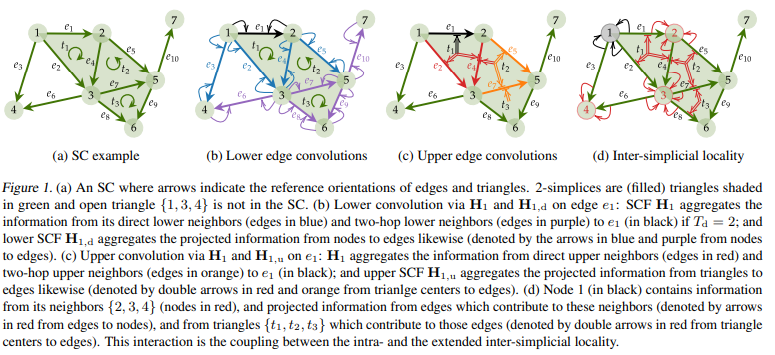
• Fig 1에서 제안 모델 SCCNNs의 학습 메커니즘을 잘 나타내주고 있습니다. 밑에 설명을 읽어보면, 주어진 Simplicial complex (SC)에 대하여 다음의 Lower & Upper edge 정보를 가지고 있는 H_k (k : SC의 차원) 행렬을 기반으로 타겟 엣지 e_1를 업데이트 하고자 합니다. 다음을 수식적으로 표현하면 아래와 같습니다.

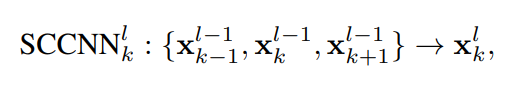
• 구체적으로, 각각의 x는 (l-1)번째 레이어에서 (k-1 & + 1) - simplex (or Face & Co-face element)들을 동일한 차수의 simplex를 받아 아래의 식 1를 따라 업데이트합니다. 여기에서 \sigma 기호는 비선형 함수를 의미합니다. 여기에서 차수가 k-1, k , k+1로 다른 요소들을 활용해야 하기 때문에, 여기에서 Boundary operator B_{k, k+1}을 활용하여 이들의 포함관계를 인코딩합니다.

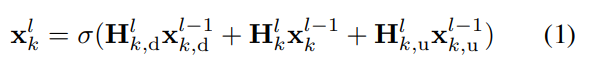
• 여기에서 H는 저자들이 선행 연구로 설계하였던 Simplicial Convolutional Filter (SCF)으로 정의됩니다. 자세한 내용은 해당 논문을 읽어보시는 것을 추천드립니다만, 이 글에서는 간단하게 해당 필터의 정의 수식만 아래에 남겨두도록 하겠습니다.
• 다음 필터 함수는 k-lower & upper Laplacian (L_k,d & L_k,u)를 인자로 받아 학습 가능한 l번째 레이어 가중치 벡터와의 선형 결합 꼴로 최대 필터 차수 T_d, T_u 만큼 반복적으로 합산 연산을 수행합니다.

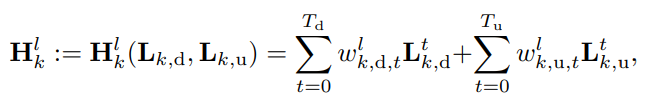
• 추가 설명을 덧붙이자면, 여기에서 H_k는 위의 식과 같이 두가지 lower & upper Laplacian 행렬을 모두 입력으로 받아 연산을 수행하지만, H_k,d 및 H_k,u 와 같은 특수 행렬의 경우 각각 lower Laplacian 및 upper Laplacian 행렬만을 입력으로 받아 연산을 수행한다는 사실을 기억하셔야 합니다. 즉 각각의 H_k는 해당 요소들로부터 독립적으로 정보를 받아 위의 식과 같이 연산한다는 사실을 꼭 이해하셔야 합니다.
• Lower edge convolution : 필터 차수가 2인 경우를 고려하여 (T_d = 2), 위의 내용으로부터 Lower edge convolution 연산은 Fig 1(b)와 같이, 타겟 e_1의 lower adj 요소인 노드 1, 2를 기반으로 이들과 연결된 엣지들 (파란색 표기)과 2-hop 떨어진 노드 3,4,5를 기반으로 이들과 연결된 엣지들 (보라색 표기)을 중심으로 필터 연산이 수행됩니다.
• Upper edge convolution : 마찬가지로 Upper edge convolution 연산은 Fig 1(c)와 같이, 타겟 e_1의 upper adj 요소인 면 t1를 기반으로 다음 면을 구성하는 엣지들 (빨간색 표기) 및 2-hop 떨어진 면 t2를 기반으로 다음 면을 구성하는 엣지들 (주황색 표기)을 중심으로 필터 연산이 수행됩니다. 여기에서 e_7의 부분은 t3의 면을 구성하기도 하기 때문에 다음 면으로부터의 정보를 전달받을 수 있습니다.
• 그렇다면 Fig 1(d)에서 보여주는 Inter-simplicial locality는 무엇을 의미하는 것일까요? 다음은 기존 모델과 비교하여 제안하는 SCCNN 모델의 차별성을 갖게 하는 Novelty가 되겠습니다.
  • 위에서 설명 드렸듯이, SNNs은 동일한 차수의 Simplex들만을 고려하여 이들과 인접한 요소들끼리만 컨볼루션 연산을 수행합니다.
  • 하지만, SCCNN은 식 2와 같이 정의되는 (다른 차수의) Simplices 사이의 Locality를 반영하여 다른 차수의 멀리 떨어진 multi-hop 요소들까지도 모두 집계할 수 있다는 이점을 가지고 있습니다. 즉, Fig 1(d)의 설명과 같이 타겟 노드 1을 업데이트 하는 데 다음 이점을 활용하면 멀리 떨어진 엣지 및 그 엣지로부터 구성되는 면의 정보들까지 모두 고려할 수 있다는 것입니다.

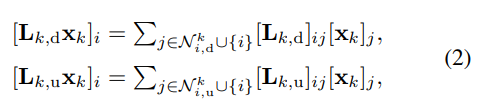
• 식 2를 보시면, 우항의 [L_k,d & L_k,u]_{i,j}이 결국 인접 Simplice들의 lower & upper adj 요소들을 고려하는 사실을 인코딩하고 있습니다. 결과적으로 k-simplice는 (k-1) & (k-2)... - simplex 들의 정보를 재귀적으로 집계하여 포괄적으로 업데이트 연산이 가능하다는 사실과, 해당 연산의 Locality 성질이 잘 유지되는 것을 이해해볼 수 있겠습니다.
• 또한 본인의 요소 i까지 j에 포함되는 경우를 고려하기 때문에 intra-locality 까지 함께 coupling한다는 사실도 중요하다는 점, 놓치지 마시기 바랍니다.

Simplicial Complex Symmetry

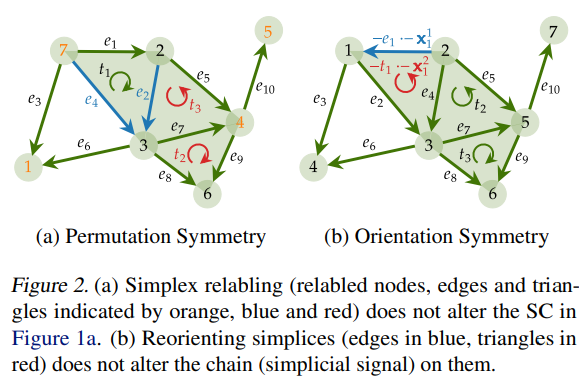
• SC의 대칭성에 대하여 SCCNN의 포착 가능한 성질을 자세하게 설명합니다. 자세한 내용은 생략하고, 결론적으로 Fig 2(a)의 Permutation 혹은 Relabeling 작업에 대해서와 Fig 2(b)의 Orientation 변동 (방향성의 부호 변화) 에 대해서도 SCCNN의 강건성을 입증합니다.
• 또한 위의 두가지 대칭성에 대하여 데이터 도메인 및 신호 도메인 상에서 SCCNNs의 동치성(equivariance)을 입증합니다. 즉, GNNs의 적용 도메인에 따라 다르게 사용될 수 있는 부분을 (e.g. 전자 : Spatial GNN, 후자 : Spectral GNN) SCCNNs은 한번에 커버 가능하다는 사실을 보입니다. 따라서 위의 도메인에서 요구하는 SC의 inductive bias를 유용하게 채택할 수 있다는 장점을 갖게 됩니다.

Spectral Analysis

• (지겹게 오마카세에서 말씀드리는) Hodge Decomposition을 기반으로 Signal Space 상에서의 SCCNN의 Spectral properties를 논의합니다. 가볍게 리마인드 해보면, Hodge Theory에 근거하여 3가지 독립적 공간으로 주어진 데이터 공간을 분해할 수 있으며 각각의 공간에서 취할 수 있는 Higher-order 특징들을 계층적으로 활용할 수 있습니다. 다음 공간의 명칭은 각각 Gradient- & Curl & Harmonic space이며, 수식적으로 다음과 같이 정의됩니다.

• 다음 관점에서 k-simplex (일반적으로 k=1, Edge space로 생각합니다.)에 대한 k-1 (node space, N으로 표기) 및 k+1 (triangle space, T로 표기) simplex의 관계 정보를 신호 공간 상에서 독립적으로 분리하여 활용해볼 수 있습니다. 다음 사실을 SCCNN의 각 레이어에서 잘 포착해낼 수 있습니다.
• 그래프 푸리에 변환 (GFT)의 이론에 근거하여, SC 상에서의 푸리에 변환을 유사하게 정의할 수 있습니다. 왜냐하면 그래프는 k=0, 즉 0-simplex 의 경우인 SC의 하위 요소로 볼 수 있기 때문입니다. 다음 사실로부터 쉽게 Simplicial Fourier Transform (SFT)를 아래와 같이 정의할 수 있습니다.

• 정말 단순하게, GFT의 정의 수식에 graph Laplacian (0th Hodge Laplacian)을 k차-Hodge Laplacian으로 확장시키어 정의하면 됩니다. 다음 행렬은 graph Laplacian 행렬과 마찬가지로 semi- positive definite하기 때문에 고유분해를 통해 고유함수 (U - 고유기저 행렬, \Lambda - 고유값 대각행렬)들을 얻을 수 있습니다.
• Hodge decomposition을 통해 3가지 직교 공간 상에서 정의되는 각각의 고유기저에 대한 스펙트럼 속성들은 아래의 Proposition 5.3의 설명으로 대체하겠습니다. Image & Kernel space에 대한 각 공간의 특성들이 다음 공간을 span하는 고유기저들 상에 잘 녹여져 있음을 확인할 수 있습니다.

• GFT에서 frequency 요소를 인코딩하는 graph Laplacian의 고유값 속성을 그대로 상속받아, SFT를 통한 고유값 행렬에서는 다른 차수들 간의 Face & Co-Face의 관점에서 이들의 Signal difference(Variance)를 측정할 수 있습니다. 그로부터 2가지 타입의 Frequencies (Gradient- , Curl frequency)를 얻을 수 있습니다.
  • Gradient frequency : Gradient space에서의 variance를 표현합니다. 즉, 네트워크 상에 흘러가는 정보의 (i.e. netflow) 노드 간 변동 (total divergence) 관점에서 엣지 상의 smoothness (or similarity)를 측정합니다.
    • 유사한 신호 혹은 특징을 갖는 두 노드 사이를 연결하는 엣지의 유사도 신호를 포착하는 것으로 생각하시면 좋을 것 같습니다.
  • Curl frequency : Curl space에서의 variance를 표현합니다. 즉, 삼각형 면 상에서 순환하는 정보 (circulation)에서 각 면을 구성하는 엣지 상 흐름의 smoothness를 측정합니다.
• 그렇다면, 다음의 신호적 특성을 분석을 위해 lower & upper Laplacian 행렬에 SFT를 적용하여 해당 스펙트럼 공간으로 맵핑하는 방법을 정의해야 합니다. Gradient- & Curl space 상으로의 다음 방식은 아래의 식 5로 공식화됩니다.

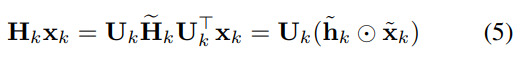
• Hat 기호는 스펙트럼 공간으로 맵핑된 신호 x 및 필터 H(: 대각 행렬)를 의미합니다.
• 3가지 공간으로 맵핑되는 입력 신호 및 필터 각각에 대하여 해당 고유값 벡터를 활용하여 아래와 같이 주파수 응답 (frequency response)를 정의할 수 있습니다.

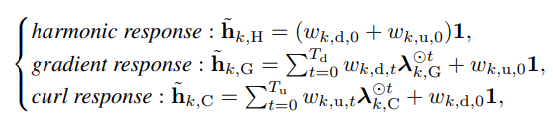
• Gradient & curl response 각각의 우항 식을 자세히 살펴보면, 먼저 Gradient response에서는 lambda_k,G는 lower weight, w_k,d에 초점을 맞추고 upper weight, w_k,u 에는 큰 초점을 두지 않고 있습니다. Curl response는 그와 반대의 경우에 해당합니다.
• 즉, 다음은 아래의 식 4와 같이 lower adj 요소들은 Gradient space으로 맵핑되며 upper adj 요소들은 Curl space으로 맵핑되어 위의 주파수 응답을 출력함을 알 수 있습니다.
• Fig 1(d)의 inter-simplicial locality (식 2)을 아래의 식 4와 같이 shifting operation을 적용함으로써 최종적으로 SCCNN의 (Spectral) Convolutional operation을 정의할 수 있게 됩니다.

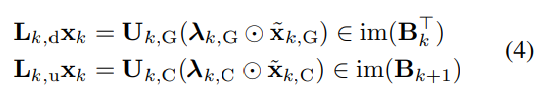
• SCCNN의 컨볼루션을 정의하는 것으로부터, 식 1의 업데이트 과정에서 비선형 함수 적용 전 단계까지 이해할 수 있게 되었습니다. 그렇다면 식 7의 각 컨볼루션 결과 (hat_y)들에 비선형성을 부여하는 함수를 적용하는 단계만 남게 되었는데요.
• Gradient (G), Curl (C), Harmonic (H)의 독립적인 속성들을 각각 얻어내어 이들을 처리할 수 있어야 하므로, 다음 함수를 적용하는 과정에서 고려해야 할 사항이 있으며 그로부터 기존 SNNs의 컨볼루션과 차별화된 속성을 얻어낼 수 있게 됩니다.

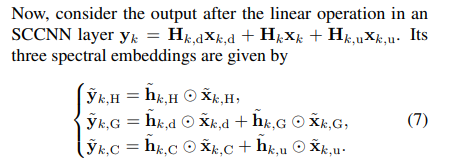
• Gama et al. (2020)의 연구를 통해, 다음 비선형성 부여는 정보 유출 효과 (information spillage)를 만들어내어, 동일한 차수의 스펙트럼 임베딩을 다른 차수의 주파수 요소들로 확산시킬 수 있다는 놀라운 사실을 내포하고 있습니다.
  • 다음 사실은 inter-simplicial locality의 특성에 부합하여 하나의 노드 업데이트에 엣지 및 면들의 포괄적인 정보를 포함할 수 있다는 사실을 입증할 수 있습니다.
  • 해당 논문의 제목인 안정성(Stability property)인 점을 고려하여, 비선형성을 도입할 때 얻을 수 있는 SC의 안정성도 한번 고려해보도록 합시다.

Stability Analysis

• 저자들은 다음 세션에서 다른 simplices (e.g. 노드, 엣지, 면)의 각각의 출력에 대한 lower & upper adj 요소들 및 inter-simplicial couplings의 여러가지 효과들을 이해하기 위해, 특정 perturbation domain 상에서 제안 SCCNNs의 안정성을 논의합니다.
• 다음 세션의 설명을 이해하기 위해 위의 선행 연구 (Gama et al.) 논문을 이해하는 것이 필수입니다. (그렇지 않으면 꽤 어렵다는 느낌을 받을 수 있습니다.. 저자가 그랬습니다.) 다음 글에서는 자세한 설명은 생략하고, 2가지 관점으로부터 SCCNNs의 안정성을 보장하는 결론을 얻을 수 있음을 설명합니다.
  • 본 논문에서 저자들이 설명하는 핵심 문장들을 아래와 같이 남겨두도록 하겠습니다. 혹시나 자세한 이해 및 설명을 원하시는 독자분들께서는 선행 논문 및 해당 세션 설명을 읽어보시는 것을 추천드립니다 !

• 긴 글 읽어주셔서 감사합니다. 이번 주 오마카세는 Simplicial complex 상의 다른 차수들 간의 메세지 집계 과정을 활용할 수 있는 컨볼루션 연산 기반의 제안 SCCNN 모델과 그 특성에 대하여 전달해드렸습니다. Simplices의 다른 차원을 고려하는 것이 학습 메커니즘 정의 및 모델 설계 부분에 있어서 여전히 어려운 문제로 남아있지만, Fig 1에서 보시다시피 직관적으로 쉽게 이해할 수 있는 아이디어를 제안하고 기존 SNNs에 비하여 상대적인 이점들을 가질 수 있다는 부분이 인상깊었던 것 같습니다.
• 정보 흐름(information flow)의 관점에서, Real world data의 inductive bias가 잘 반영될 수 있는 1-simplex (Edge) 기반의 네트워크 데이터에 특화된 모델로 많이 제안되어져왔지만, 그 이상의 2- & 3-simplex 등 에서 여러가지 환경 조건 상에 활용해볼 수 있는 장점이 있을 것으로 생각됩니다.
  • 다음은 Simplicial complex의 강력한 제약 조건인 면 들의 형태가 반드시 삼각형이어야 하는 점에서 수많은 한계점들이 존재할 것으로 생각됩니다.
  • 실제로도 2-simplex가 반드시 삼각형일 필요는 없을 것이며, 다른 형태의 면으로 표현되었을 때 더욱 효과적일 경우들이 많을 것입니다. 다음 사실에 기반하여 발전된 Cell complex이 최근 각광을 받고 있는 것으로 알고 있습니다.
  • 허나, Simplicial complex의 중요한 배경이 되는 호몰로지 이론과 그로부터 구축된 higher-order complex의 잠재성 등은 절대 무시할 수 없는 사실입니다 !
• 글을 마무리하기에 앞서, 그래프 오마카세를 함께 만들어나갈 마음이 있으신 분들을 구하고 있습니다. 매주 다양한 그래프 주제로 자유롭게 뉴스레터를 연재하는 것에 관심이 있으신 분들께서는 언제든지 제 메일주소로 편하게 연락주시면 감사하겠습니다 !

[Contact Info]

Gmail : jhbae1184@akane.waseda.jp

Twitter (X): @jhbae1184

LinkedIn